Гипергеометрическое распределение.

 

Случайная величина Х имеет гипергеометрическое распределение с параметрами  а, b, п, если ее возможные значения  0, 1, 2, … п  имеют вероятности

                         (16)

На практике гипергеометрическое распределение возникает при следующих условиях: имеется а объектов одного вида и b – другого, всего этих объектов (а+ b) штук. Из них выбирают (в отличие от биноминального закона) без возврата п штук. Случайная величина Х – число т объектов вида  (или ), среди отобранных. При этом:  

                   (17)

Пример 5

Фирма имеет 6 предприятий, среди которых 2 дочерних. Для налоговой проверки выбирают 3 предприятия. Составить закон распределения случайной величины Х-числа дочерних предприятий, среди трех отобранных.

Решение

Случайная величина Х может принимать следующие значения: 0, 1, 2, 3. Вероятности этих значений найдем по формуле (16). Поскольку дочерних предприятий у фирмы два, то вероятность значения Х=3 равна 0, как вероятность невозможного события.  Получим закон распределения вероятностей, представленный в таблице 10.

 

Таблица 10 – Закон распределения вероятностей в примере 5.

Х	0	1	2	3
Р				0

 

 

Непрерывные случайные величины

Основные понятия и вероятностные характеристики.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка, или более строго: случайная величина Х называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду,  кроме, быть может, отдельных точек. Очевидно, что число возможных значений непрерывной случайно величины бесконечно. Задать непрерывную случайную величину можно с помощью функции распределения , но такое задание не является  единственным. Непрерывная величина полностью характеризуется плотностью распределения вероятностей

Плотностью распределения вероятностей непрерывной случайной величины называется функция  

, при этом                    (18)

Площадь фигуры, ограниченной кривой распределения 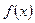 и осью абсцисс равна единице.

 , в частности,                     (19)

     Функция распределения F( x) выражается через плотность распределения формулой:

                                                                  (20)

     Вероятность того, что случайная величина X принимает значение в заданном числовом промежутке, определяется формулой:

                                        (21)

Математическим ожиданием непрерывной случайной величины Х называется её среднее значение, вычисляемое по формуле:

.                  (22)

Дисперсия непрерывной случайной величины Х определяется по формуле:

           (23)

Среднее квадратическое отклонение равно

Пример 6.

Задана функция распределения F(x). 1) Найти параметр а.2)Найти . 3)Построить графики  и .

F (x) =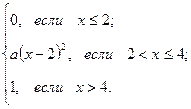

Решение

1) Для определения коэффициента а, используем свойство непрерывности функции F( x).

           

2) Так как , то:

=

 

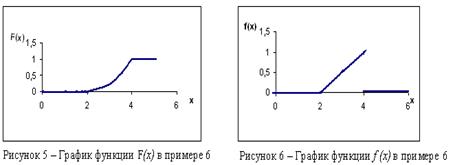
3) Для построения графиков функций F( x) и f ( x) используем элементарные функции и их свойства. Функция F( x) – квадратичная на промежутке (2;4] и её графиком является парабола ( рисунок 5). Функция f ( x) – линейная на промежутке (2;4] и ее графиком является прямая линия ( рисунок 6).

 

 

Пример 7.

Дана плотность распределения вероятностей

                              (x)=   

Требуется: 1) Найти а. 2) Найти функцию распределения . 3) Построить графики  и . 4)Найти вероятность попадания случайной величины на промежуток(2;3).

Решение

1) Определим  коэффициент а, используя свойство плотности распределения (19) . Из условия , получим:

2) Поскольку функция распределения F (x) выражается через плотность распределения формулой (20), то найдем её на каждом указанном в примере промежутке.

Если , то

Если , то

.

 

Если , то

. 

Таким образом,

3) Для построения графиков функций  и  используем элементарные функции.  - квадратичная на промежутке (2;4] и её график представлен на рисунке 7.  - на промежутке  (2;4]  изображена частью кубической гиперболы (рисунок 8).

 

 

4) Вероятность попадания случайной величины Х на промежуток (2;3) можно найти двумя способами: по формулам (3) и  (21).

, или:

.

 

       Пример 8

       Найти математическое ожидание М(Х) и дисперсию D(Х), если случайная величина Х имеет плотность распределения вероятностей  в интервале (4;9), а  вне его - .

Решение.

Используем формулы (22) и (23):

 

.

.

     При решении практических задач встречаются различные законы распределения непрерывных случайных величин. Рассмотрим некоторые из них.