 |
Главная |
Геометрическая интерпретация комплексного числа.
|
из
5.00
|
Теоретический материал для подготовки к самостоятельной работе
Раздел 1 Теория чисел
Комплексные числа. Основные понятия и определения. Решение многих задач сводится к решению алгебраических уравнений. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов математики. Стремление сделать уравнение разрешимым - одна из главных причин расширения понятия числа.Рациональные и иррациональные числа образуют множество R действительных чисел. Однако действительных чисел недостаточно для того, чтобы решить уравнение. Корень уравнения  или
или  называется мнимой единицей и обозначается буквой i. Таким образом, символ iудовлетворяет условию
называется мнимой единицей и обозначается буквой i. Таким образом, символ iудовлетворяет условию

Комплексным числом называется число видаa+bi, где aи b – действительные числа, а i- мнимая единица. Число а называется действительной частью комплексного числа, а число bi – мнимой частью. Запись комплексного числа в виде z= a+bi называется алгебраической формой записи комплексного числа. Два комплексных числа  и
и  называются равными тогда и только тогда, когда равны их действительные части и коэффициенты при мнимой части.
называются равными тогда и только тогда, когда равны их действительные части и коэффициенты при мнимой части.
Понятия«больше» и «меньше» для комплексных чисел не определяются.
Комплексные числа a+bi и a-biназываются сопряжёнными, а комплексные числаa+bi и -a-bi называются противоположными комплексными числами.
Действия над комплексными числами в алгебраической форме.
Суммой двух комплексных чисел  и
и  называется комплексное число
называется комплексное число  .
.
Произведением двух комплексных чисел  называется комплексное число.
называется комплексное число.
Вычитание комплексных чисел вводится как операция, обратная сложению; деление комплексных чисел как операция, обратная умножению. При делении на комплексное число достаточно умножить числитель и знаменатель дроби  на число сопряжённое знаменателю
на число сопряжённое знаменателю 
Пример 1. Найти сумму и разность комплексных чисел  и
и  .
.
Решение. Сумму находим сложением двучленов  :
:

Произведение находим перемножением двучленов  с последующей заменой
с последующей заменой  на -1.
на -1. 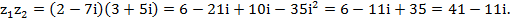
Пример 2. Даны комплексные числа  и
и  . Найти разность
. Найти разность  и частное
и частное  .
.
Решение. Разность находим формальным вычитанием двучленов  и
и  :
:

Чтобы найти частное  , умножим числитель и знаменатель этой дроби на число, сопряженное знаменателю
, умножим числитель и знаменатель этой дроби на число, сопряженное знаменателю  :
:

Геометрическая интерпретация комплексного числа.
Комплексное число  изображается на координаиной плоскости точкой
изображается на координаиной плоскости точкой  или вектором
или вектором  , начало которого совпадает с началом координат, а конец – с точкой
, начало которого совпадает с началом координат, а конец – с точкой  .
.

Координатная плоскость называется при этом комплексной плоскостью, ось абсцисс – действительной ось, а ось ординат – мнимой осью.
Модулем комплексного числа  называется абсолютная величина вектора, соответствующего этому числу. Для модуля числа
называется абсолютная величина вектора, соответствующего этому числу. Для модуля числа  используются обозначения
используются обозначения 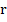 ,
,  На основании теоремы Пифагора получается формула
На основании теоремы Пифагора получается формула 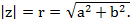
Например, комплексное число 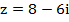 имеет модуль, равный 10, так как
имеет модуль, равный 10, так как  .
.
Аргументом комплексного числа  называется величина угла
называется величина угла 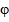 между положительным направлением действительной оси и вектором, соответствующим этому числу. Аргумент комплексного числа z= a+bi можно находить так:
между положительным направлением действительной оси и вектором, соответствующим этому числу. Аргумент комплексного числа z= a+bi можно находить так:
а) найти острый угол 
б) найти аргумент комплексного числа в зависимости от того, в какой координатной четверти лежит вектор, соответствующий этому числу: в 1 четверти  ; во 2 четверти
; во 2 четверти  ; в 3четверти
; в 3четверти 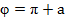 ; в 4 четверти
; в 4 четверти  .
.
Пример 3. Найдите аргумент комплексного числа  .
.
Решение. Находим угол  . Вектор, соответствующий данному комплексному числу, лежит в 4 координатной четверти, поэтому аргументом числа является
. Вектор, соответствующий данному комплексному числу, лежит в 4 координатной четверти, поэтому аргументом числа является  . Аргументы действительных и чисто мнимых чисел надо находить непосредственно, исходя из их геометрической интерпретации, а, не используя приведенное выше правило.
. Аргументы действительных и чисто мнимых чисел надо находить непосредственно, исходя из их геометрической интерпретации, а, не используя приведенное выше правило.
Тригонометрическая форма комплексного числа. Пусть дано комплексное число  . Можно выразить действительные числа
. Можно выразить действительные числа  через модуль
через модуль  числа
числа 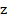 следующим образом:
следующим образом:  Таким образом, комплексное число можно записать в виде
Таким образом, комплексное число можно записать в виде  где
где  модуль комплексного числа, a
модуль комплексного числа, a  один из его аргументов. Представление комплексного числа
один из его аргументов. Представление комплексного числа  в указанном виде называется тригонометрической формой записи комплексного числа. Чтобы перейти от алгебраической формы записи комплексного числа
в указанном виде называется тригонометрической формой записи комплексного числа. Чтобы перейти от алгебраической формы записи комплексного числа 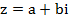 к тригонометрической, достаточно найти его модуль и аргумент. Аргумент комплексного числа
к тригонометрической, достаточно найти его модуль и аргумент. Аргумент комплексного числа 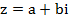 можно находить из системы
можно находить из системы 
Пример 4. Записать число  в тригонометрической форме.
в тригонометрической форме.
Решение. Находим модуль  .
.
Находим угол  . Вектор, соответствующий данному комплексному числу, лежит в 3 координатной четверти. Аргументом является
. Вектор, соответствующий данному комплексному числу, лежит в 3 координатной четверти. Аргументом является  Следовательно
Следовательно  Что бы перейти от тригонометрической формы записи комплексного числа
Что бы перейти от тригонометрической формы записи комплексного числа  к алгебраической, достаточно найти действительные числа
к алгебраической, достаточно найти действительные числа 
Пример 5. Записать число  в алгебраической форме.
в алгебраической форме.
Решение. Сначала найдем  и
и  :
:

 Следовательно,
Следовательно, 
Действия над комплексными числами, заданными в тригонометрической форме. Если 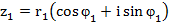 и
и  , то
, то 
 Если
Если  то
то


где  – арифметический корень,
– арифметический корень, 
Пример 6. Даны комплексные числа  Найти их произведение и частное. Ответ записать в алгебраической форме.
Найти их произведение и частное. Ответ записать в алгебраической форме.
Решение. Применим правила умножения и деления комплексных чисел


Пример 7.Вычислить  .
.
Решение. Находим z 
Пример 8. Вычислить  . Решение. Запишем число
. Решение. Запишем число  в тригонометрической форме. Находим
в тригонометрической форме. Находим


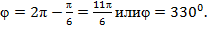 Тогда
Тогда 
Пример 9. Вычислить  Ответ записать в тригонометрической и алгебраической формах.
Ответ записать в тригонометрической и алгебраической формах.
Решение. Запишем число -81 в тригонометрической форме:
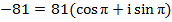 . Следовательно,
. Следовательно,

При 
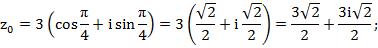



Показательная форма комплексного числа.
Рассматривая функцию  для комплексного переменного, Эйлер установил соотношение
для комплексного переменного, Эйлер установил соотношение 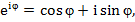 которое называется формулой Эйлера.
которое называется формулой Эйлера.
Из этой формулы следует, что каждое комплексное число  можно записать в форме
можно записать в форме  которая называется показательной формой записи. Над комплексными числами, заданными в показательной форме, удобно производить умножение и деление, возведение в натуральную степень и извлечение корня:
которая называется показательной формой записи. Над комплексными числами, заданными в показательной форме, удобно производить умножение и деление, возведение в натуральную степень и извлечение корня: 


Пример 10. Представить число 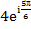 в алгебраической форме.
в алгебраической форме.
Решение. По условию,  откуда
откуда  Значит,
Значит, 
Пример 11. Выполнить действия и записать ответ в тригонометрической и показательной формах:

Решение. Сначала выполним действия:

Теперь запишем число в тригонометрической и показательной формах, для чего найдем модуль и аргумент:  Тогда
Тогда  .
.
|
из
5.00
|
Обсуждение в статье: Геометрическая интерпретация комплексного числа. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

