 |
Главная |
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
|
из
5.00
|
Уравнение 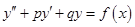 , ,
|
где 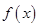 - заданная функция, а
- заданная функция, а 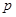 и
и 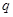 - числовые (постоянные) коэффициенты называется неоднородным линейным дифференциальным уравнением второго порядка с постоянными коэффициентами.
- числовые (постоянные) коэффициенты называется неоднородным линейным дифференциальным уравнением второго порядка с постоянными коэффициентами.
Если 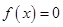 , то уравнение принимает вид:
, то уравнение принимает вид:
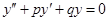 . .
|
называется однородным линейным, дифференциальным уравнением второго порядка.
Общее решение уравнения имеет вид:
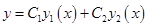 , ,
|
где 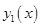 и
и 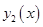 - линейно независимые функции, удовлетворяющие уравнению, (т.е. являющиеся решениями этого уравнения) а
- линейно независимые функции, удовлетворяющие уравнению, (т.е. являющиеся решениями этого уравнения) а 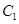 и
и 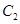 - произвольные постоянные.
- произвольные постоянные.
Частное решение уравнения будем искать в виде функции
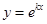 . .
|
где 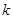 - действительное или комплексное число, подлежащее определению
- действительное или комплексное число, подлежащее определению
Имеем: 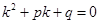 . .
|
Алгебраическое уравнение называется характеристическим уравнением однородного уравнения. Характеристическое уравнение дает возможность найти 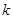 . Уравнение есть уравнение второй степени и потому имеет два корня. Обозначим их через
. Уравнение есть уравнение второй степени и потому имеет два корня. Обозначим их через 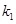 и
и 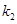 . Возможны три случая.
. Возможны три случая.
1)Корни 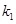 и
и 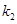 действительные и различные(
действительные и различные( 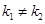 ). В этом случае получим два частных решения уравнения
). В этом случае получим два частных решения уравнения 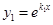 ,
, 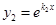 , которые являются линейно независимыми. Общее решение уравнения:
, которые являются линейно независимыми. Общее решение уравнения: 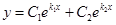 .
.
Пример 12.Найти общее решение уравнения 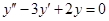 .
.
Решение. Составим характеристическое уравнение: 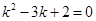 . Оно имеет два различных действительных корня
. Оно имеет два различных действительных корня 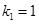 и
и 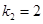 . Поэтому общее решение есть
. Поэтому общее решение есть 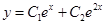 .
.
2) Корни 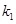 и
и 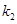 действительные и равные
действительные и равные 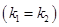 ,то частное решение выразится функцией
,то частное решение выразится функцией 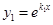 ,
, 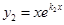 . Заметим, что решения
. Заметим, что решения 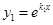 и
и 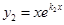 линейно независимы. Следовательно, общее решение
линейно независимы. Следовательно, общее решение 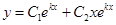 или
или 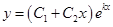
Пример 13.Найти общее решение уравнения 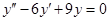 .
.
Решение. Составим характеристическое уравнение: 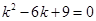 . Оно имеет два равных корня
. Оно имеет два равных корня 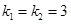 . Поэтому общее решение есть
. Поэтому общее решение есть 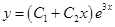 .
.
3) Корни 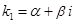 и
и 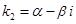 – комплексные. То общее решение уравнения будет иметь вид
– комплексные. То общее решение уравнения будет иметь вид 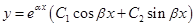 .
.
Пример 14. Найти общее решение уравнения 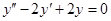 .
.
Решение. Составим характеристическое уравнение:
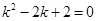 . Оно имеет комплексные корни
. Оно имеет комплексные корни 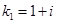 ,
, 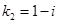 , где
, где 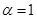 ,
, 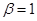 . Поэтому общее решение есть
. Поэтому общее решение есть 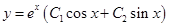 .
.
Интегральное исчисление
Функция F ( x ) называется первообразной для функции f ( x ), если ( F ( x ))’=f ( x ).
Первообразная определена неоднозначно: если F ( x ) – первообразная для функции f ( x ), то F ( x )+ C – также первообразная для данной функции.
Множество всех первообразных для функции f ( x ) называется неопределенным интегралом и обозначается 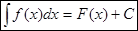 , где f ( x ) – подынтегральная функция, f ( x ) dx – подынтегральное выражение, С – произвольная постоянная (С = const),
, где f ( x ) – подынтегральная функция, f ( x ) dx – подынтегральное выражение, С – произвольная постоянная (С = const), 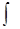 - знак операции интегрирования, d – знак операции дифференцирования.
- знак операции интегрирования, d – знак операции дифференцирования.
Свойства неопределенного интеграла:
1. 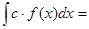
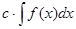 , где с = const. 2.
, где с = const. 2. 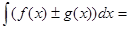
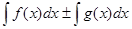 .
.
3. 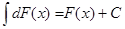 .
.
Таблица 1 (неопределенных интегралов)
1. 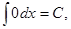 2.
2. 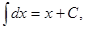 3.
3. 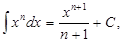 n ≠ –1;
4. n ≠ –1;
4. 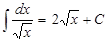 ;
5. ;
5. 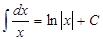 ;
6. ;
6. 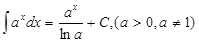 ;
7. ;
7. 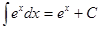 ;
8. ;
8. 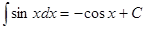 ; ;
| 9. 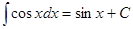 ;
10. ;
10. 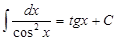 11.
11. 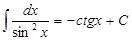 ;
12. ;
12. 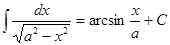 (|x|<a, a≠0);
13. (|x|<a, a≠0);
13. 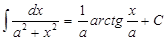 (a≠0);
14. (a≠0);
14. 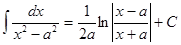 (|x|≠a, a≠0);
15. (|x|≠a, a≠0);
15. 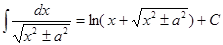 . .
|
Найти неопределенный интеграл:
а) 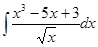 ; б)
; б) 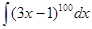 ; в)
; в) 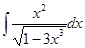 ; г)
; г) 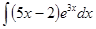 .
.
Решение: а) 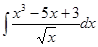 ,чтобы найти данный неопределенный интеграл, воспользуемся методом разложения, который заключается в разложении подынтегральной функции на сумму функций и использовании свойств неопределенного интеграла 1 и 2.
,чтобы найти данный неопределенный интеграл, воспользуемся методом разложения, который заключается в разложении подынтегральной функции на сумму функций и использовании свойств неопределенного интеграла 1 и 2.
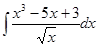 =
= 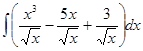 =
= 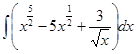 =(св-во 2) =
=(св-во 2) =
= 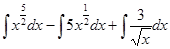 = (св-во 1) =
= (св-во 1) = 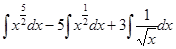 =(используем формулы 3 и 4 из таблицы 1)=
=(используем формулы 3 и 4 из таблицы 1)= 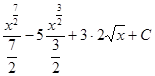 =
= 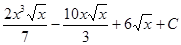 .
.
Ответ: 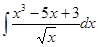 =
= 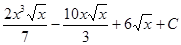 .
.
б) 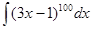 . Данный интеграл вычисляется методом замены переменной (линейная замена). Обозначим выражение в скобках через t: 3х – 1 = t, тогда d(3х – 1)=dt => 3d х = dt =>
. Данный интеграл вычисляется методом замены переменной (линейная замена). Обозначим выражение в скобках через t: 3х – 1 = t, тогда d(3х – 1)=dt => 3d х = dt => 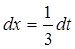 .
.
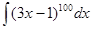 =
= 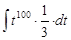 =
= 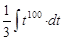 = (по формуле 3 из таблицы 1 н.и.) = =
= (по формуле 3 из таблицы 1 н.и.) = = 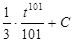 =
= 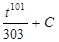 =
= 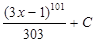 . Ответ:
. Ответ: 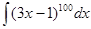 =
= 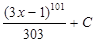 .
.
в) 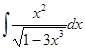 . Здесь при вычислении интеграла используется также метод замены переменной (нелинейная замена).
. Здесь при вычислении интеграла используется также метод замены переменной (нелинейная замена). 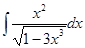 =
= 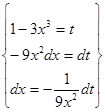 =
= 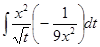 =
= 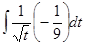 =
= 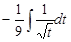 =(используем формулу 4 из табл.1)=
=(используем формулу 4 из табл.1)= 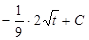 =
= 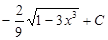 .
.
Ответ: 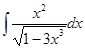 =
= 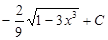 .
.
Определённый интеграл
Для вычисления определенных интегралов используется формула Ньютона-Лейбница: 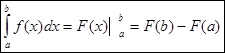 , (где а – нижний предел интегрирования, b – верхний предел, F(x) – первообразная для функции f(x)). Для нахождения первообразной F(x) используются те же методы, что и при вычислении неопределенных интегралов.
, (где а – нижний предел интегрирования, b – верхний предел, F(x) – первообразная для функции f(x)). Для нахождения первообразной F(x) используются те же методы, что и при вычислении неопределенных интегралов.
Решение.
а) 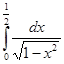 = (формула 9 табл. 1) =
= (формула 9 табл. 1) = 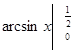 =
=  .
.
Ответ: 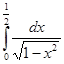 =
= 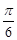 .
.
б) Используем метод замены переменной: 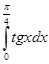 =
= 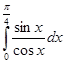 =
=
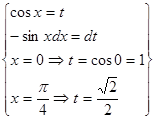 =
= 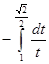 = (по формуле 3 табл.1 н.и.)=
= (по формуле 3 табл.1 н.и.)= 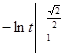 =
= 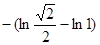 = (т.к. ln1 = 0)=
= (т.к. ln1 = 0)= 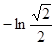 =
= 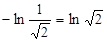 . Ответ:
. Ответ: 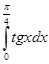 =
= 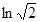 .
.
Замечание: В отличие от метода замены для неопределенных интегралов, для определенных интегралов нет необходимости возвращаться к старой переменной интегрирования (х), если перейти к новым пределам интегрирования (в нашем примере старыми пределами были а = 0, b = 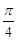 , а новыми стали а = 1, b =
, а новыми стали а = 1, b = 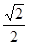 ).
).
|
из
5.00
|
Обсуждение в статье: Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

