Линейные дифференциальные уравнения первого порядка

Уравнение ,

где и –заданные функции, называется линейным дифференциальным уравнением первого порядка.

Решение уравнения будем искать в виде произведения

двух неизвестных функций и 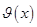. Подстановка дает 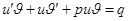. После преобразований получаем

.

Выражение в круглых скобках в уравнении приравняем нулю:

, тогда следует равенство

.

Далее можно найти функцию 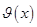и подставить в уравнение и решать его относительно второй неизвестной функции .

Разделяя переменные в уравнении и интегрируя, последовательно получаем: 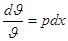, , откуда

с .

Подстановка функции 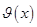 дает

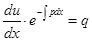, откуда .

Интегрируя последнее равенство, находим вторую неизвестную функцию

.

Возвращаясь к подстановке, находим общее решение уравнения

.

Полученное соотношение можно рассматривать как формулу, дающую общее решение уравнения при заданных функциях  и .

Пример 8. Найти общее решение уравнения .

Решение. Это линейное дифференциальное уравнение первого порядка, в котором 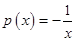, . Подставляем эти выражения для 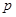 и 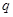в формулу и, вычисляя соответствующие интегралы, получаем

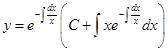= = . Таким образом, – общее решение исходного уравнения.

Пример 9. (Закон перехода вещества в раствор.)

Рассмотрим процесс перехода вещества в раствор. Известно, что при фиксированной температуре количество вещества, содержащееся в определенном объеме растворителя, не может превзойти некоторого, определенного для каждого вещества числа , соответствующего насыщенному раствору. Известно также, что по мере приближения к насыщенному раствору уменьшается количество вещества, переходящего в раствор за единицу времени. Иными словами, чем больше вещества перешло в раствор, тем меньше скорость перехода.

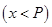Решение. Пусть  — количество вещества, перешедшего в раствор к моменту времени . Тогда  — скорость перехода, и в соответствии со сказанным можно написать: , где стремится к нулю при , .Эксперименты показывают, что для многих веществ функция  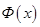пропорциональна разности , т.е. , и, следовательно,

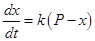, где 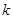> 0 – коэффициент пропорциональности.

Далее преобразуем уравнение к виду .

Это – линейное дифференциальное уравнение первого порядка.

Далее имеем:

Пусть -момент времени, с которого начался процесс перехода вещества в раствор. Очевидно, . Поэтому , откуда 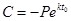, и, значит,

.

Ответ: 

Значения 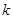 и 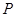 определяются характером растворенного вещества и растворителя. Значит при любых  и 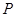 величина стремится к 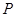, если . Вид функции  хорошо согласуется с экспериментальными данными. Поэтому формулу можно рассматривать как закон перехода вещества в раствор.

Пример 10. Конденсатор емкостью 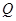 включается в цепь с напряжением и сопротивлением 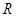. Определить заряд 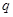конденсатора в момент после включения.

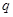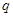Решение. Сила  электрического тока представляет производную от количества электричества , прошедшего через проводник, по времени . В момент  заряд конденсатора и сила тока ; в цепи действует электродвижущая сила Е, равная разности между напряжением цепи и напряжением конденсатора , т. е. Согласно закону Ома . 

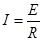Поэтому 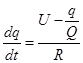 .Отсюда: . Теперь согласно формуле имеем:

.

По условию при  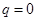и потому  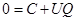и 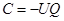. Таким образом, в момент времени . Ответ: .

Дифференциальные уравнения второго порядка. Дифференциальное уравнение второго порядка, разрешенное относительно у", имеет вид:

.

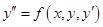В общее решение уравнения второго порядка входят две произвольные постоянные 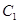и 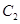.Функция , удовлетворяющая уравнению, на­зывается его общим решением.

Рассмотрим два частных случая, когда уравнение второго порядка сводится к дифференциальному уравнению первого порядка.

1) Пусть в правой части уравнения отсутствует функция  и ее производная , т.е. уравнение имеет вид

.

В результате двукратного последовательного интегрирования получаем общее решение этого уравнения:

.
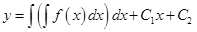2) Пусть в правой части уравнения 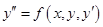отсутствует функция т.е. уравнение имеет вид .

В этом случае обозначим , тогда . Подстановка этих выражений в уравнение приводит его к уравнению первого порядка вида

.

общим решением этого уравнения будет функция 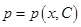. Отсюда получаем уравнение  или .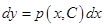

Интегрируя последнее соотношение, получим общее решение уравнения .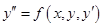

Пример 11.Найти частное решение дифференциального уравнения 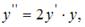если .

Решение. Это дифференциальное уравнение второго порядка. В записи уравнения нет переменной x. Можно сделать подстановку: Тогда:

Получаем:

Проинтегрировав обе части равенства получим: Найдем значение свободной переменной.

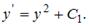По условию: если х =0, то y =1и y’=2. 2=1²+C₁. C₁=1.

Найдем значение свободной переменной. По условию: если х =0, то y=1. Получили:

Ответ: