 |
Главная |
Соответствия между множествами.
|
из
5.00
|
Соответствием между множествами X и Y, называется любое подмножество декартова произведения  .Поскольку соответствие– это подмножество, то его можно задать как любоемножество, т.е. либо перечислив все пары элементов, находящихся в данном соответствии, либо указав характеристическое свойство элементов этого подмножества.
.Поскольку соответствие– это подмножество, то его можно задать как любоемножество, т.е. либо перечислив все пары элементов, находящихся в данном соответствии, либо указав характеристическое свойство элементов этого подмножества.
Например, соответствие между множествами X={1, 2, 4, 6} и Y={3, 5} можно задать:1) при помощи предложения с двумя переменными: a<b при условии, что a 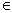 X, b
X, b 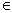 Y;2) перечислив пары чисел, принадлежащих подмножеству декартова произведения X
Y;2) перечислив пары чисел, принадлежащих подмножеству декартова произведения X  Y: {(1, 3),(1, 5), (2, 3), (2, 5), (4, 5)}. К этому способу задания относят также задание соответствия при помощи графа и графика.
Y: {(1, 3),(1, 5), (2, 3), (2, 5), (4, 5)}. К этому способу задания относят также задание соответствия при помощи графа и графика.
3.2 Основы теории графов
Графом в математике называется конечная совокупность точек, называемых вершинами графа; некоторые из них соединены друг с другом линиями, которые называются ребрами графа. График соответствия представляет собой изображение множества X  Y в виде точек на координатной плоскости. Представление соответствия в виде графа и графика позволяет изображать его в тех ситуациях, когда в заданном соответствии находится бесконечное множество пар чисел. Например: А= {1, 2, 3}, B = {1, 2, 3, 4, 5, 6}.
Y в виде точек на координатной плоскости. Представление соответствия в виде графа и графика позволяет изображать его в тех ситуациях, когда в заданном соответствии находится бесконечное множество пар чисел. Например: А= {1, 2, 3}, B = {1, 2, 3, 4, 5, 6}.
 Пусть задано соответствие R между множествами Х и У, т.е. R:
Пусть задано соответствие R между множествами Х и У, т.е. R:  ,
,  ,
, 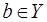 . Для некоторого элемента а из множества Х поставлен в соответствие некоторый элемент в множества У. Тогда элемент в называется образом элемента а, а элемент а – прообразов элемента в. Может случиться, что из данной точки не выходит ни одна стрелка, например, b. Тогда образ элемента b пуст. Множество Х называют областью отправления соответствия R, множество У – областью прибытия. Совокупность всех элементов из Х, имеющих непустые образы, называют множеством определения соответствия R. Множество всех элементов из У, имеющих непустой полный прообраз, называют множеством значений соответствия R.
. Для некоторого элемента а из множества Х поставлен в соответствие некоторый элемент в множества У. Тогда элемент в называется образом элемента а, а элемент а – прообразов элемента в. Может случиться, что из данной точки не выходит ни одна стрелка, например, b. Тогда образ элемента b пуст. Множество Х называют областью отправления соответствия R, множество У – областью прибытия. Совокупность всех элементов из Х, имеющих непустые образы, называют множеством определения соответствия R. Множество всех элементов из У, имеющих непустой полный прообраз, называют множеством значений соответствия R.
 Отношения порядка. Упорядоченное множество с небольшим числом элементов наглядно представляется ориентированным графом. При этом элементам множества M сопоставляются вершины графа (обозначаются на рисунке точками), а элементам отношения a - дуги (линии со стрелками). Например, на рисунке приведен ориентированный граф, представляющий отношение
Отношения порядка. Упорядоченное множество с небольшим числом элементов наглядно представляется ориентированным графом. При этом элементам множества M сопоставляются вершины графа (обозначаются на рисунке точками), а элементам отношения a - дуги (линии со стрелками). Например, на рисунке приведен ориентированный граф, представляющий отношение  = {(a, a), (a, b), (a, c), (b, c)} на множестве M = {a, b, c, d}.
= {(a, a), (a, b), (a, c), (b, c)} на множестве M = {a, b, c, d}.
Задать порядок на множестве можно различными способами. Так, например, в таблице приведено три способа упорядочения четырех стран.
| Площадь | Россия | США | Франция | Англия |
| Население | США | Россия | Франция | Англия |
| Плотность населения | Англия | Франция | США | Россия |
На рисунке приведены ориентированные графы, представляющие отношения "делится" и "меньше" на множестве M = {1, 2, 3, 4} натуральных чисел.


Теория графов в последнее время широко используется в различных отраслях науки и техники, особенно в экономике и социологии. Основы теории графов разработал Л. Эйлер, решавший задачу о разработке замкнутого маршрута движения по мостам в г. Кенигсберге. При решении задачи он обозначил каждую часть суши точкой, а каждый мост – линией, их соединяющей. В результате был получен граф (рис.1).Эйлер доказал, что такая задача решения не имеет.
 Эйлер Леонард (1707–1783) швейцарский математик, механик, физик, астроном. Автор более 800 работ по различным разделам математики и другим наукам. Быстрое развитие теория графов получила с созданием электронно-вычислительной техники, которая позволяла решить многие задачи алгоритмизации. Пусть на плоскости задано некоторое множество вершин X и множество U соединяющих их дуг. Графом называют бинарное отношение множества X и множеств U: G= = (X;U),или, иначе ƒ:X → К. Здесь ƒ – отображение инциденций. Граф называется ориентированным, если указано направление дуг и неориентированным, если такое направление не указано. Примером неориентированного графа является карта дорог. Граф называется петлей, если его начало и конец совпадают. Две вершины называются смежными, если существует соединяющая их дуга.
Эйлер Леонард (1707–1783) швейцарский математик, механик, физик, астроном. Автор более 800 работ по различным разделам математики и другим наукам. Быстрое развитие теория графов получила с созданием электронно-вычислительной техники, которая позволяла решить многие задачи алгоритмизации. Пусть на плоскости задано некоторое множество вершин X и множество U соединяющих их дуг. Графом называют бинарное отношение множества X и множеств U: G= = (X;U),или, иначе ƒ:X → К. Здесь ƒ – отображение инциденций. Граф называется ориентированным, если указано направление дуг и неориентированным, если такое направление не указано. Примером неориентированного графа является карта дорог. Граф называется петлей, если его начало и конец совпадают. Две вершины называются смежными, если существует соединяющая их дуга.
Ребро uj называется инцидентным вершине хj, если оно выходит или входит в вершину.
Степенью (валентностью) вершины называется число инцидентных ей ребер. Кратностью пары вершин называется число соединяющих их ребер или дуг.
Подграфом Ga графа G называется граф, в который входит лишь часть вершин графа G вместе с дугами их соединяющими. Частным графом Gb графа называется граф, в который входит лишь часть дуг графа G вместе с вершинами их соединяющими. Карта шоссейных дорог это граф. Дороги Саратовской области это подграф, а главные дороги – это частный граф. Путем в графе G называется такая последовательность дуг, в которой конец каждой последующей дуги совпадает с началом предыдущей. Длиной пути называют число входящих в этот путь дуг. Путь может быть конечным и бесконечным. Путь, в котором никакая дуга не встречается дважды, называется элементарным.
Контур– это конечный путь, у которого начальная и конечная вершины совпадают. Контур называется элементарным, если все его вершины различны (кроме начальной и конечной). Контур единичной дуги называется петлей. В неориентированном графе понятие дуга, путь, контур заменяются соответственно на ребро, цепь, цикл.
Ребро – отрезок, соединяющий две вершины, цепь– последовательность ребер.
Цикл – конечная цепь, у которой начальная и конечная вершина совпадают.
Граф называется связанным, если любые его две вершины можно соединить цепью. Граф сильно связан, если для его двух любых вершин хi≠хj существует путь, идущий из хi и хj. Граф, который не является связанным, может быть разбит на конечное число связных графов, называемых компонентами, или частями .Ребро графа G называется мостом, если граф, полученный из G путем удаления этого ребра, имеет больше компонент связности, чем граф G. Точкой сочленения графа называется вершина, удаление которой приводит к увеличению числа его компонент связности.
На рисунке 3 ребро к– мост, а на рисунке 4 вершина 1 – точка сочленения.
| 
|
|
Неразделимым называется связный граф, не имеющий точек сочленения. Блоком графа называют максимальный неразделимый подграф. На рисунке 5 приведен граф G и его блоки А, В, С и D.

Дерево это конечный, связный, не ориентированный граф, не имеющий циклов. Характеристическое свойство деревьев состоит в том, что любые две вершины дерева соединены единственной цепью. Теория деревьев была, в основном, разработана Кирхгофом. Он применил ее для решения систем линейных уравнений, описывающих работу электрических цепей. Кирхгоф Густав (1824–1887) немецкий физик, механик, математик. Развитие теории графов (деревьев) связано с именем немецкого химика Кели, который успешно применил ее для решения задач органической химии (для изучения изомеров углеводородов с заданным числом атомов).Совокупность деревьев называется лесом. Если все вершины графа принадлежат дереву, то он называется покрывающим. Пусть дано множество вершин графа. Одну из вершин, например х1, примем за начальную, которую назовем корнем дерева. Из этой вершины проводим ребра к остальным вершинам х2, х3 и т.д. Простейшее дерево состоит из двух вершин, соединенных ребром. Если добавить ребро, то добавляется и вершина. Таким образом, дерево с п вершинами имеет n-1 ребро. Дерево имеет корень в вершине ,если существует путь от х1, к каждой из вершин. Ребра графа, принадлежащие дереву, называют ветвями, остальные ребра называют хордами.

Рассмотрим подробно решение задачи о Кенигсбергских мостах. В городе Кенигсберге имеется остров Кнайпхоф, который охвачен двумя рукавами реки Пречель.


Через два рукава перекинуты семь мостов: а, Ь, с, d, e, ƒ, g. Можно ли спланировать прогулку таким образом, чтобы по каждому мосту пройти только один раз и вернуться в начальное положение? Поставим в соответствие каждому мосту ребро графа, а суше вершину (рис. 11).
Эйлеровым путем в графе G называется такой путь, в котором каждое ребро встречается один раз. Эйлер доказал, что такой путь существует тогда и только тогда, когда граф G содержит не более двух вершин нечетной степени и являются связными. В данной задаче существует четыре вершины нечетной степени (5, 3, 3, 3). Таким образом, задача о Кенигсбергских мостах не содержит Эйлеров путь и не имеет решения.
Если граф содержит точно две вершины нечетной степени, то в Эйлеровом пути эти вершины должны быть конечными.
Если вершин нечетной степени нет, то граф имеет замкнутый Эйлеров путь.
На рисунке 12, а нет замкнутого Эйлерова пути; на рисунке 12, б Эйлеров путь замкнут.

 Теорема 4. (теорема Эйлера). В любом конечном графе сумма степеней вершин равна удвоенному числу его ребер. В XIX в. Гамильтон придумал игру, состоящую в том, что на доске располагались города в виде додекаэдра.
Теорема 4. (теорема Эйлера). В любом конечном графе сумма степеней вершин равна удвоенному числу его ребер. В XIX в. Гамильтон придумал игру, состоящую в том, что на доске располагались города в виде додекаэдра.
Играющий (игрок) должен обозначить шнуром замкнутый круг, соединяющий последовательно одну вершину с другой, посетив при этом все города, зайдя в каждый только один раз. Граф G называют Гамильтоновым, если он содержит простейший путь, проходящий через его вершину.
Задача о коммивояжере принадлежит к классу задач математического программирования. Требуется найти такой путь коммивояжера, по которому необходимо посетить и-1 городов, зайдя в каждый город, вернуться домой, причем протяженность пути должна быть минимальной. Таким образом, среди всех гамильтоновых циклов графа с п вершинами нужно найти сумму длин ребер, путь по которым будет минимальным. Математически эта задача решения не имеет.
Дерево игры – это способ описания игры, в которой последовательно, по ходам, фиксируется, какой информацией должны располагать игроки, какие варианты они могут выбрать, а также средний размер платежей в конце игры. Игра, описываемая при помощи такого дерева, называется игрой в развернутой форме или позиционной игрой.
Дерево решений – это система, отражающая структуру оптимизации задачи принятия решений. Ветви – это события, которые имеют место, а вершины – состояния в которых возникает проблема выбора. Узлы выбора различны. В одних решения принимает руководитель, в других выбор производит «природа», т.е. выбор ситуации от руководителя не зависит и он может только оценить вероятность принятия того или иного решения. Дерево решений применяется тогда, когда количество альтернатив и принятых решений конечно.
Построение деревьев решений используют при решении задач динамического распределения памяти ЭВМ. В динамическом программировании решение задачи планирования работ называют проектом. Нужно выбрать наилучший проект за заданное время с использованием выделенных ресурсов. Существуют два способа решения этой задачи: 1) Метод кратчайшего пути. 2) Проект оценки и пересмотра проекта.
Характерным для этих методов является изображение проекта в виде сети
взаимосвязанных работ.
Взвешенный ориентированный граф без петель, в котором выделено k-вершин, называемых полюсами, является k-полюсной цепью. Среди сетей особо выделяется двухполюсная транспортная сеть (рис. 14) S=(N, U) с множеством вершин N и множеством дуг U, для которых выполняется следующее условие:
1) существует только одна вершина сети s є N, в которую не заходит ни одна дуга. Эта вершина называется входом, или истоком сети;
2) существует только одна вершина сети t є N, из которой не выходит ни одной дуги сети. Эта вершина называется выходом, или стоком сети;
3) каждой дуге сети u є U поставлено в соответствие неотрицательное число с(u), называемое пропускной способностью дуги.

Примерами вершин сети могут быть пересечения автострад, электростанции, телефонные узлы, железнодорожные узлы, аэропорты, водохранилища, товарные склады.
Примерами дуг сети могут быть дороги, линии электропередачи, телефонные линии, авиалинии, водные магистрали, нефте - и газопроводы.
Постановку и решение подобных задач можно получить с помощью методов сетевого моделирования.
|
из
5.00
|
Обсуждение в статье: Соответствия между множествами. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


