 |
Главная |
Дифференциальное и интегральное исчисления. Обыкновенные дифференциальные уравнения.
|
из
5.00
|
Последовательности. Основные понятия и определения. Рассмотрим ряд натуральных чисел:1, 2, 3, … ,n–1, n, … .
Если заменить каждое натуральное число n в этом ряду некоторым числом un, следуя некоторому закону, то мы получим новый ряд чисел: u1, u2, u3, …, un - 1, un, …, кратко обозначаемый {un} и называемый числовой последовательностью. Величина un называется общим членом последовательности. Обычно числовая последовательность задаётся некоторой формулой un=f(n), позволяющей найти любой член последовательности по его номеру n; эта формула называется формулой общего члена. Заметим, что задать числовую последовательность формулой общего члена не всегда возможно; иногда последовательность задаётся путём описания её членов (см. ниже последний пример).
Примеры числовых последовательностей: 1, 2, 3, 4,5, …- ряд натуральных чисел;2, 4, 6, 8, 10, …-ряд чётных чисел; 1.4, 1.41, 1.414, 1.4142, …- числовая последовательность приближённых значений 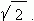 с увеличивающейся точностью.
с увеличивающейся точностью.
В последнем примере невозможно дать формулу общего члена последовательности, тем не менее, эта последовательность описана полностью. Предел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение.
 Это определение означает, что a есть предел числовой последовательности, если её общий член неограниченно приближается к a при возрастании n. Геометрически это значит, что для любого
Это определение означает, что a есть предел числовой последовательности, если её общий член неограниченно приближается к a при возрастании n. Геометрически это значит, что для любого  >0 можно найти такое число N, что начиная с n>N все члены последовательности расположены внутри интервала (a-
>0 можно найти такое число N, что начиная с n>N все члены последовательности расположены внутри интервала (a-  , a+
, a+  ). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.
). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.
Последовательность называется ограниченной, если существует такое число M, что |un|  M для всех n. Возрастающая или убывающая последовательность называется монотонной.
M для всех n. Возрастающая или убывающая последовательность называется монотонной.
Теорема Вейерштрасса. Всякая монотонная и ограниченная последовательность имеет предел.
Основные свойства пределов. Нижеприведенные свойства пределов справедливы не только для числовых последовательностей, но и для функций.
Если {un} и {vn}- две сходящиеся последовательности, то:

Некоторые замечательные пределы:

Дифференциальное исчисление. Производная.
Определение. Производной функции  в точке
в точке 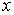 называется
называется  .
.
Из определения следуют правила дифференцирования:
-
 ;
; -
 где
где  ;
; -
 ;
; -
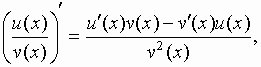 где
где  ;
; -
 ;
;  где
где  ;
; -
 ,
,  ;
; -
 при
при 
 ; в частности,
; в частности,  ;
; -
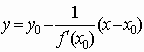 ; в частности,
; в частности, 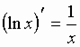 ;
; -
 ;
; -
 ;
; -
 ;
;
Дифференциальные уравнения – это уравнения, содержащие производные некоторой функции  . В дальнейшем вместо слов дифференциальное уравнение будем писать ДУ.
. В дальнейшем вместо слов дифференциальное уравнение будем писать ДУ.
Если ДУ содержит обычные производные функции одной переменной, то оно называется обыкновенным дифференциальным уравнением.
Если уравнение содержит частные производные функции нескольких переменных, то оно называется ДУ в частных производных. Рассмотрим обыкновенные дифференциальные уравнения. Исходя из этого определения, в качестве примеров, рассмотрим три простых дифференциальных уравнения:
 , ,
| (1) | |||
 , ,
| (2) | |||
|
| (3) | |||
ДУ может содержать также производные различных порядков, выше первого:  , . . . ,
, . . . ,  . Например, уравнение
. Например, уравнение

| (4) |
содержит производную второго порядка  , а уравнение
, а уравнение
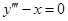
| (5) |
содержит производную третьего порядка  . Самый высокий порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Поэтому уравнения (1), (2) и (3) это ДУ первого порядка, а уравнения (4) и (5) это ДУ второго и третьего порядков соответственно.
. Самый высокий порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Поэтому уравнения (1), (2) и (3) это ДУ первого порядка, а уравнения (4) и (5) это ДУ второго и третьего порядков соответственно.
Решением ДУ называется функция  , которая обращает это уравнение в тождество. График решения на плоскости
, которая обращает это уравнение в тождество. График решения на плоскости  называется интегральной кривой. Например, решением уравнения
называется интегральной кривой. Например, решением уравнения  (2) является функция
(2) является функция  (6), график которой (интегральная кривая)представляет собой параболу. Если к правой части равенства (6) прибавить любое число (например,
(6), график которой (интегральная кривая)представляет собой параболу. Если к правой части равенства (6) прибавить любое число (например,  ), то функция также будет решением уравнения (2).
), то функция также будет решением уравнения (2).
В этом случае решение определяется с точностью до произвольной постоянной.
Множество решений  +С, где С - произвольная постоянная, называется общим решением ДУ.
+С, где С - произвольная постоянная, называется общим решением ДУ.
Например, общее решение уравнения (2) имеет вид
 . .
| (7) |
Это решение, содержащее одну произвольную постоянную, является общим решение ДУ первого порядка (2). Очевидно, что решением уравнения  (1) является любая постоянная. Таким образом, общее решение уравнения (1) можно записать в виде
(1) является любая постоянная. Таким образом, общее решение уравнения (1) можно записать в виде
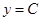 . .
| (8) |
Подставляя конкретные значения постоянной  , будем получать решения уравнения, которые называются частными решениями. Используя понятие производной второго порядка, перепишем уравнение
, будем получать решения уравнения, которые называются частными решениями. Используя понятие производной второго порядка, перепишем уравнение  (4) в виде
(4) в виде  (9)
(9)
Тогда аналогично уравнению (2), получим 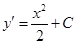 (10) И далее
(10) И далее  (11)
(11)
Это общее решение уравнения второго порядка (4), содержит две произвольные постоянные.
Аналогично можно найти общее решение ДУ третьего порядка 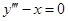 (5):
(5):
 (12) Оно содержит три произвольные постоянные.
(12) Оно содержит три произвольные постоянные.
Решить уравнение  (3) сложнее. Для этого нужно использовать один из методов решения ДУ первого порядка.
(3) сложнее. Для этого нужно использовать один из методов решения ДУ первого порядка.
Дифференциальные уравнения первого порядка. В общем случае ДУпервого порядка содержит независимую переменную 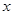 , неизвестную функцию
, неизвестную функцию  и производную первого порядка этой функции
и производную первого порядка этой функции  . В общем виде ДУ первого порядка можно представить так:
. В общем виде ДУ первого порядка можно представить так:
 . .
| (13) |
Примером записи ДУ в форме (13) является уравнение 
Если из соотношения (13) можно выразить  в виде
в виде
 , ,
| (14) |
такая форма записи ДУ называется уравнением, разрешенным относительно производной. В качестве примера, из уравнения (3) выразим  , получим
, получим
 . .
| (15) |
В уравнении (15)  . Функция
. Функция  , удовлетворяющая уравнению (14) и содержащая одну произвольную постоянную, называется общим решением этого уравнения. Часто это решение можно получить только в неявной форме
, удовлетворяющая уравнению (14) и содержащая одну произвольную постоянную, называется общим решением этого уравнения. Часто это решение можно получить только в неявной форме

| (16) |
или
 . .
| (17) |
В этом случае соотношение (16) или (17)называется общим интегралом уравнения  . Решить или проинтегрировать данное дифференциальное уравнение — значит найти его общее решение в той или иной форме. Постоянную
. Решить или проинтегрировать данное дифференциальное уравнение — значит найти его общее решение в той или иной форме. Постоянную  можно найти, если задано начальное условие – значение искомой функции в некоторой точке
можно найти, если задано начальное условие – значение искомой функции в некоторой точке
 . .
| (18) |
Здесь  это некоторое известное число. Решение, которое получается из общего решения при некотором фиксированном значении произвольной постоянной
это некоторое известное число. Решение, которое получается из общего решения при некотором фиксированном значении произвольной постоянной  , называется частным решением. Задача отыскания решения ДУ
, называется частным решением. Задача отыскания решения ДУ  (14), удовлетворяющего начальному условию
(14), удовлетворяющего начальному условию  (18), называется задачей Коши. ДУ первого порядка может быть записано также в форме:
(18), называется задачей Коши. ДУ первого порядка может быть записано также в форме:
 . .
| (19) |
Отметим, что формы записи уравнений (14) и (19) эквивалентны. От записи уравнения в форме (14) можно перейти к записи в виде (19) и наоборот.
Уравнения с разделяющимися переменными. Пусть ДУ первого порядка записано в виде  (14). Это уравнение называется уравнением с разделяющимися переменными, если функция
(14). Это уравнение называется уравнением с разделяющимися переменными, если функция  имеет вид
имеет вид
 , ,
| (20) |
то есть представляет собой произведение функции только от переменной 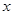 на функцию только от
на функцию только от  . В этом случае уравнение записывается в виде
. В этом случае уравнение записывается в виде
 . .
| (21) |
“Разделение переменных” заключается в приведении уравнения (22) к виду (разделили на  и умножили на
и умножили на  )
)
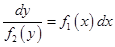 . .
| (23) |
Общее решение получается в результате интегрирования
 . .
| (24) |
Пример 1. Решить уравнение  .
.
Решение. Перепишем, используя другое обозначение для производной  . Разделение переменных приводит к равенству
. Разделение переменных приводит к равенству  .
.
В результате вычисления интегралов  , получаем
, получаем  , откуда
, откуда  . Ответ.
. Ответ.  ; где
; где  – произвольная постоянная.
– произвольная постоянная.
Пример 2. Решить уравнение  .
.
Решение. Перепишем уравнение в виде  . Разделение переменных приводит к равенству
. Разделение переменных приводит к равенству  . В результате вычисления интегралов
. В результате вычисления интегралов  получаем
получаем 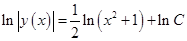 ,где
,где  - произвольная положительная постоянная. Произвольная постоянная записана в форме
- произвольная положительная постоянная. Произвольная постоянная записана в форме  для удобства записи формы общего решения. Далее, используя свойства логарифмов, из последнего равенства получаем
для удобства записи формы общего решения. Далее, используя свойства логарифмов, из последнего равенства получаем  .
.
Отсюда 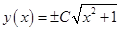 , где
, где  .Отрицательные и неотрицательные решения охватываются одной формулой:
.Отрицательные и неотрицательные решения охватываются одной формулой:  ,
,  - произвольная постоянная.
- произвольная постоянная.
Ответ.  ;
;  - произвольная постоянная.
- произвольная постоянная.
Если ДУ первого порядка записано в виде (20), то оно будет уравнением с разделяющимися переменными, если функции  и
и  можно представить в виде произведений
можно представить в виде произведений
 ,
,
 ,
,
в которых сомножители зависят только от одной переменной. Тогда уравнение (20) перепишется в следующей форме:
 . .
| (25) |
Деля уравнение (6.24) на произведение  (предполагаем, что оно не равно нулю), получаем:
(предполагаем, что оно не равно нулю), получаем:
 . .
| (25) |
Заметим, что в уравнении (25) множитель перед  — функция только одной переменной
— функция только одной переменной  , а множитель перед
, а множитель перед  — функция только одной переменной
— функция только одной переменной  .
.
Уравнение 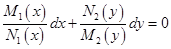 (25) называется уравнением с разделенными переменными. Общим интегралом уравнения (25) является соотношение
(25) называется уравнением с разделенными переменными. Общим интегралом уравнения (25) является соотношение
 . .
| (26) |
Пример 3.Решить уравнение  .
.
Решение. Интегрируя, находим  . Здесь постоянная интегрирования обозначена
. Здесь постоянная интегрирования обозначена  , так как левая часть последнего равенства неотрицательна. Умножая последнее равенство на 2, получаем
, так как левая часть последнего равенства неотрицательна. Умножая последнее равенство на 2, получаем  . Это уравнение семейства концентрических окружностей с центром в начале координат и радиусом
. Это уравнение семейства концентрических окружностей с центром в начале координат и радиусом  .
.
Пример 4. Решить уравнение  .
.
Решение. Разделяя переменные, получим:  .
.
Интегрируя последнее уравнение, будем иметь:  , где
, где  . Произвольная постоянная записана как
. Произвольная постоянная записана как  для удобной записи общего решения. Используя формулу для суммы логарифмов и потенцируя последнее равенство, получим
для удобной записи общего решения. Используя формулу для суммы логарифмов и потенцируя последнее равенство, получим  . Если считать
. Если считать  , то это решение можно записать
, то это решение можно записать  . Это же решение описывается равенством
. Это же решение описывается равенством  , в котором
, в котором  произвольная постоянная любого знака. Это семейство прямых, проходящих через начало координат.
произвольная постоянная любого знака. Это семейство прямых, проходящих через начало координат.
Пример 5. Решить задачу Коши

Решение:  ;
;

 + С, для удобства С=lnC
+ С, для удобства С=lnC 

 – общее решение уравнения.
– общее решение уравнения.
Найдем частное решение, удовлетворяющее условию  .
. 
 . Подставим найденное значение:
. Подставим найденное значение:  ,
,  ,
,  ,
,  – решение задачи Коши.
– решение задачи Коши.
Пример 6 .(Задача об охлаждении тела.)
Скорость охлаждения тела в воздухе пропорциональна разности между температурой тела и температурой воздуха. Температура воздуха равна 20° С. Известно, что в течение 20 мин тело охлаждается от 100 до 60° С. Определить закон изменения температуры в теле в зависимости от времени I .
Решение. Согласно условию задачи имеем:
 , где k- коэффициент пропорциональности. Разделяя переменные и интегрируя, получаем
, где k- коэффициент пропорциональности. Разделяя переменные и интегрируя, получаем
 ,
,  , что после потенцирования дает
, что после потенцирования дает  , следовательно,
, следовательно,  общее решение уравнения.
общее решение уравнения.
Для определения  используем начальное условие: при
используем начальное условие: при 
 . Отсюда:
. Отсюда: 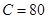 . Поэтому
. Поэтому 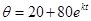 . Коэффициент пропорциональности k определяем из дополнительного условия: при
. Коэффициент пропорциональности k определяем из дополнительного условия: при 
 . Отсюда:
. Отсюда: 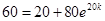 или
или  и, следовательно
и, следовательно 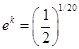 . Итак, искомая функция
. Итак, искомая функция  .
.
Однородные уравнения первого порядка. Уравнение вида  (14)называется однородным уравнением первого порядка, если функция
(14)называется однородным уравнением первого порядка, если функция  представляется в виде функции, зависящей только от величины:
представляется в виде функции, зависящей только от величины:  =
=  .
.
Пример 7.Найти общее решение уравнения  .
.
Решение.  ,
, 
 ,
,  ,
,  ,
,
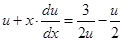 ,
,  ,
,
 ,
,
 ,
,
 ,
,
 ,
,  ,
,  ,
,  ,
,
Ответ:  , где
, где  – произвольная постоянная.
– произвольная постоянная.
|
из
5.00
|
Обсуждение в статье: Дифференциальное и интегральное исчисления. Обыкновенные дифференциальные уравнения. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

