 |
Главная |
Методы интегрирования. Метод прямоугольников. Метод трапеции. Метод Симпсона.
|
из
5.00
|
Численные методы –раздел высшей математики. Рассмотрим два метода приближенного вычисления определенного интеграла – метод трапеций и метод Симпсона. Рассмотрим пример с рисунком. Вычислить определенный интеграл 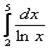
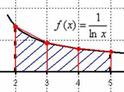
В данном примере интеграл не берётся – перед вами неберущийся, так называемый интегральный логарифм. А существует ли вообще этот интеграл. Изобразим на чертеже график подынтегральной функции 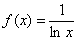 :
:
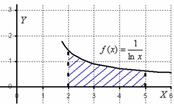 Подынтегральная функция непрерывна на отрезке
Подынтегральная функция непрерывна на отрезке 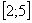 и определенный интеграл
и определенный интеграл 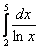 численно равен заштрихованной площади, но интеграл не берётся, на помощь приходят численные методы. При этом задача встречается в двух формулировках:
численно равен заштрихованной площади, но интеграл не берётся, на помощь приходят численные методы. При этом задача встречается в двух формулировках:
1) Вычислить определенный интеграл приближенно, округляя результат до определённого знака после запятой. Например, до двух знаков после запятой, до трёх знаков после запятой и т.д. Предположим, получился приближенный ответ 5,347, он может быть не совсем верным (в действительности, более точный ответ 5,343). Наша задача состоит лишь в том, чтобы округлить результат до трёх знаков после запятой.
2) Вычислить определенный интеграл приближенно, с определённой точностью. Например, вычислить определённый интеграл приближенно с точностью до 0,001. Это значит, что если получен приближенный ответ 5,347, то все цифры должны быть правильными. А точнее ответ 5,347 должен отличаться от истины по модулю не более чем на 0,001. Существуют несколько основных методов приближенного вычисления определенного интеграла:
Метод прямоугольников. Отрезок интегрирования разбивается на несколько частей и строится ступенчатая фигура (гистограмма), которая по площади близка к искомой площади: 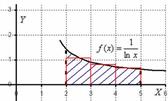 Точность построения чертежа помогает понять суть методов. В данном примере проведено разбиение отрезка интегрирования
Точность построения чертежа помогает понять суть методов. В данном примере проведено разбиение отрезка интегрирования  на три отрезка:
на три отрезка:  . Чем чаще разбиение (больше более мелких промежуточных отрезков), тем выше точность. Метод прямоугольников даёт грубое приближение площади, поэтому очень редко встречается на практике. Метод трапеций. Отрезок интегрирования разбивается на несколько промежуточных отрезков, и график подынтегральной функции приближается к ломаной линии:
. Чем чаще разбиение (больше более мелких промежуточных отрезков), тем выше точность. Метод прямоугольников даёт грубое приближение площади, поэтому очень редко встречается на практике. Метод трапеций. Отрезок интегрирования разбивается на несколько промежуточных отрезков, и график подынтегральной функции приближается к ломаной линии: 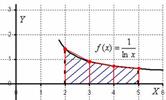
Таким образом, площадь (синяя штриховка) приближается к сумме площадей трапеций (красный цвет). Отсюда и название метода. Метод трапеций даёт значительно лучшее приближение, чем метод прямоугольников (при одинаковом количестве отрезков разбиения), чем больше более мелких промежуточных отрезков, тем выше точность. Метод трапеций чаще встречается в практических заданиях.
Метод Симпсона (метод парабол). Это более совершенный способ – график подынтегральной функции приближается не ломаной линией, а маленькими параболками. Сколько промежуточных отрезков – столько и маленьких парабол. Если взять те же три отрезка, то метод Симпсона даст ещё более точное приближение, чем метод прямоугольников или метод трапеций. Чертеж строить нет смысла, поскольку визуально приближение будет накладываться на график функции 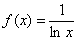 (ломаная линия предыдущего пункта –практически совпала). Задача на вычисление определенного интеграла по формуле Симпсона – самое популярное задание на практике. Вычислить определенный интеграл методом трапеций. Рассмотрим определенный интеграл
(ломаная линия предыдущего пункта –практически совпала). Задача на вычисление определенного интеграла по формуле Симпсона – самое популярное задание на практике. Вычислить определенный интеграл методом трапеций. Рассмотрим определенный интеграл 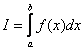 , где
, где 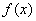 – функция, непрерывная на отрезке
– функция, непрерывная на отрезке 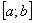 . Проведём разбиение отрезка
. Проведём разбиение отрезка 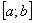 на
на 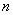 равных отрезков:
равных отрезков: 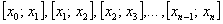 . При этом очевидно:
. При этом очевидно: 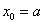 (нижний предел интегрирования) и
(нижний предел интегрирования) и 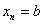 (верхний предел интегрирования). Точки
(верхний предел интегрирования). Точки 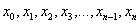 также называют узлами.
также называют узлами.
Тогда определенный интеграл можно вычислить приближенно по формуле трапеций: 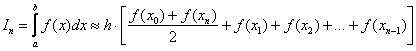 , где:
, где: 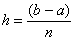 – длина каждого из маленьких отрезков или шаг;
– длина каждого из маленьких отрезков или шаг; 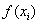 – значения подынтегральной функции в точках
– значения подынтегральной функции в точках 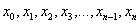 .
.
Пример 1. Вычислить приближенно определенный интеграл по формуле трапеций. Результаты округлить до трёх знаков после запятой. 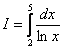 а) Разбив отрезок интегрирования на 3 части.
а) Разбив отрезок интегрирования на 3 части.
б) Разбив отрезок интегрирования на 5 частей.
Решение:
 По условию отрезок интегрирования нужно разделить на 3 части, то есть
По условию отрезок интегрирования нужно разделить на 3 части, то есть 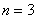 . Вычислим длину каждого отрезка разбиения:
. Вычислим длину каждого отрезка разбиения: 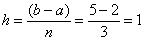 . Параметр
. Параметр 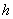 , называется шагом. Точек
, называется шагом. Точек 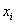 (узлов разбиения) будет на одну больше, чем количество отрезков:
(узлов разбиения) будет на одну больше, чем количество отрезков: 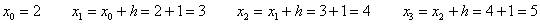
Таким образом, общая формула трапеций сокращается до малых размеров: 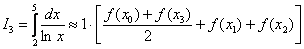 .
.
Для расчетов можно использовать обычный микрокалькулятор:
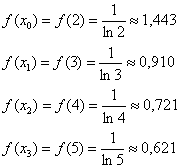 .
.
В соответствии с условием задачи, все вычисления следует округлять до 3-его знака после запятой. 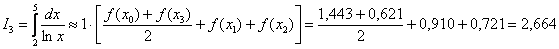
Полученное значение – это приближенное значение площади (см. рисунок выше). б) Разобьём отрезок интегрирования на 5 равных частей, то есть 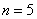 ,увеличивая количество отрезков, увеличивается точность вычислений.
,увеличивая количество отрезков, увеличивается точность вычислений.
Если 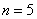 , то формула трапеций принимает следующий вид:
, то формула трапеций принимает следующий вид: 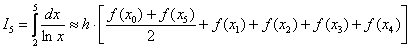 . Найдем шаг разбиения:
. Найдем шаг разбиения: 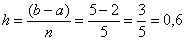 , то есть, длина каждого промежуточного отрезка равна 0,6.
, то есть, длина каждого промежуточного отрезка равна 0,6.
При оформлении задачи все вычисления удобно оформлять расчетной таблицей: 
В первой строке записываем «счётчик». Во второй строке, сначала записываем нижний предел интегрирования 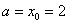 , остальные значения получаем, последовательно приплюсовывая шаг
, остальные значения получаем, последовательно приплюсовывая шаг 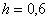 , по такому же принципу заполняется нижняя строка, Например, если
, по такому же принципу заполняется нижняя строка, Например, если 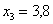 , то
, то 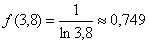 . В результате:
. В результате: 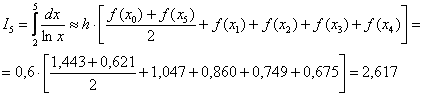 .
.
Если для 3-х отрезков разбиения 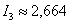 , то для 5-ти отрезков
, то для 5-ти отрезков 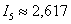 . Таким образом, можно утверждать, что
. Таким образом, можно утверждать, что 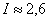 .
.
Пример 2.Вычислить приближенно определенный интеграл по формуле трапеций с точностью до двух знаков после запятой (до 0,01). 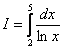
Решение: Отличие от примера 1 состоит в том, что мы не знаем, на сколько отрезков разбивать отрезок интегрирования, чтобы получить два верных знака после запятой. Иными словами, мы не знаем значение 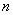 . Существует специальная формула, позволяющая определить количество отрезков разбиения, чтобы достигнуть требуемой точности. Сначала отрезок интегрирования разбивается на несколько больших отрезков, как правило, на 2-3-4-5. Разобьем отрезок интегрирования, например, на те же 5 частей. Формула:
. Существует специальная формула, позволяющая определить количество отрезков разбиения, чтобы достигнуть требуемой точности. Сначала отрезок интегрирования разбивается на несколько больших отрезков, как правило, на 2-3-4-5. Разобьем отрезок интегрирования, например, на те же 5 частей. Формула: 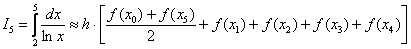
Шаг известен: 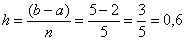 . До какого разряда округлять результаты
. До какого разряда округлять результаты 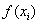 ? В условии же ничего не сказано о том, сколько оставлять знаков после запятой. Общая рекомендация такова : к требуемой точности нужно прибавить 2-3 разряда. В данном случае необходимая точность 0,01. Согласно рекомендации, после запятой оставим пять знаков (можно было и четыре):
? В условии же ничего не сказано о том, сколько оставлять знаков после запятой. Общая рекомендация такова : к требуемой точности нужно прибавить 2-3 разряда. В данном случае необходимая точность 0,01. Согласно рекомендации, после запятой оставим пять знаков (можно было и четыре):  .
.
В результате: 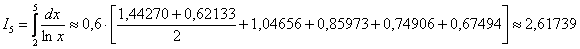
После первичного результата количество отрезков удваивают. В данном случае необходимо провести разбиение на 10 отрезков.
Для 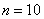 формула трапеций приобретает следующий вид:
формула трапеций приобретает следующий вид: 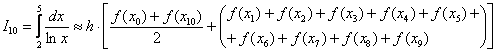 .
.
Запись можно перенести на следующую строчку.
Вычислим шаг разбиения: 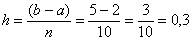 . Результаты расчётов сведём в таблицу:
. Результаты расчётов сведём в таблицу: 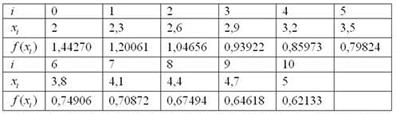
Длинную таблицу удобнее превратить в двухэтажную.
В результате: 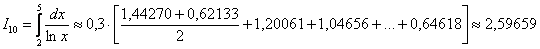
Рассчитаем, насколько улучшился результат: 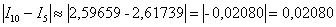
Здесь используем знак модуля, поскольку нас интересует абсолютная разность, а не какой результат больше, а какой – меньше.
Полученная оценка погрешности больше, чем требуемая точность: 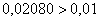 . Поэтому необходимо ещё раз удвоить количество отрезков разбиения до
. Поэтому необходимо ещё раз удвоить количество отрезков разбиения до 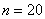 , и вычислить уже
, и вычислить уже 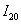 . В реальных задачах часто требуется провести разбиение отрезка на 20 частей. С помощью экселевского калькулятора готовый результат можно получить в считанные секунды:
. В реальных задачах часто требуется провести разбиение отрезка на 20 частей. С помощью экселевского калькулятора готовый результат можно получить в считанные секунды: 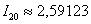 . Снова оцениваем погрешность:
. Снова оцениваем погрешность: 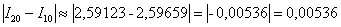 . Полученная оценка погрешности меньше, чем требуемая точность:
. Полученная оценка погрешности меньше, чем требуемая точность: 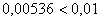 . Округлить последний (наиболее точный) результат
. Округлить последний (наиболее точный) результат 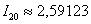 до двух знаков после запятой. Ответ:
до двух знаков после запятой. Ответ: 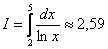 с точностью до 0,01.
с точностью до 0,01.
Вычисление определенного интеграла по формуле Симпсона. Рассмотрим определенный интеграл 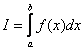 , где
, где 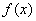 – функция, непрерывная на отрезке
– функция, непрерывная на отрезке 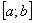 . Проведём разбиение отрезка
. Проведём разбиение отрезка 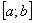 на чётное количество равных отрезков обозначив через
на чётное количество равных отрезков обозначив через 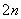 .На практике отрезков может быть: два:
.На практике отрезков может быть: два: 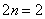 , четыре:
, четыре: 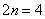 , восемь:
, восемь: 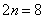 , десять:
, десять: 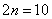 , двадцать:
, двадцать: 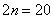 . Число
. Число 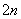 понимается как единое число. То есть, нельзя сокращать, например,
понимается как единое число. То есть, нельзя сокращать, например, 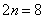 на два, получая
на два, получая 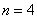 . Разбиение имеет следующий вид:
. Разбиение имеет следующий вид: 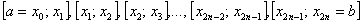 .
.
Термины аналогичны терминам метода трапеций: Точки 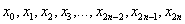 называют узлами. Формула Симпсона для приближенного вычисления определенного интеграла имеет следующий вид:
называют узлами. Формула Симпсона для приближенного вычисления определенного интеграла имеет следующий вид: 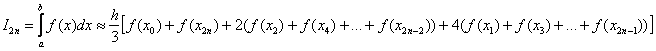
где: 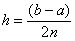 длина каждого из маленьких отрезков или шаг;
длина каждого из маленьких отрезков или шаг; 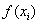 – значения подынтегральной функции в точках
– значения подынтегральной функции в точках 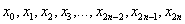 .
.
Разберём формулу подробнее: 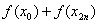 – сумма первого и последнего значения подынтегральной функции;
– сумма первого и последнего значения подынтегральной функции; 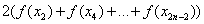 – сумма членов с чётными индексами умножается на 2;
– сумма членов с чётными индексами умножается на 2; 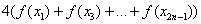 сумма членов с нечётными индексами умножается на 4.
сумма членов с нечётными индексами умножается на 4.
Пример 3. Вычислить приближенно определенный интеграл по формуле Симпсона с точностью до 0,001. Разбиение начать с двух отрезков 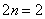
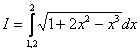 . Интеграл опять неберущийся.
. Интеграл опять неберущийся.
Решение: Необходимо вычислить определенный интеграл с определенной точностью. Как и для метода трапеций, существует формула, которая сразу позволит определить нужное количество отрезков (значение «эн») чтобы достичь требуемой точности. Необходимо найти четвертую производную и решать экстремальную задачу. На практике всегда используется упрощенный метод оценки погрешности.
Решение. Если у нас два отрезка разбиения 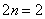 , то узлов будет на один больше:
, то узлов будет на один больше: 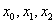 . И формула Симпсона принимает вид:
. И формула Симпсона принимает вид: 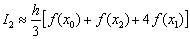 .
.
Вычислим шаг разбиения: 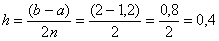 .
.
Заполним расчетную таблицу: 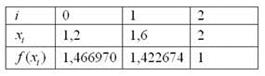
В верхнюю строку записываем «счётчик» индексов. Во второй строке сначала пишем нижний предел интегрирования 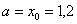 , а затем последовательно приплюсовываем шаг
, а затем последовательно приплюсовываем шаг 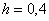 . В третью строку заносим значения подынтегральной функции. Например, если
. В третью строку заносим значения подынтегральной функции. Например, если 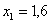 , то
, то 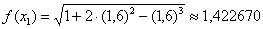 . Принцип тот же, что и в методе трапеций, смотрим на требуемую точность: 0,001. И прибавляем дополнительно 2-3 разряда. То есть, округлять нужно до 5-6 знаков после запятой. В результате:
. Принцип тот же, что и в методе трапеций, смотрим на требуемую точность: 0,001. И прибавляем дополнительно 2-3 разряда. То есть, округлять нужно до 5-6 знаков после запятой. В результате: 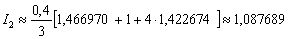 .Первичный результат получен. Теперь удваиваем количество отрезков до четырёх:
.Первичный результат получен. Теперь удваиваем количество отрезков до четырёх: 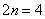 . Формула Симпсона для данного разбиения принимает следующий вид:
. Формула Симпсона для данного разбиения принимает следующий вид: 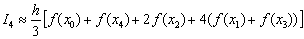 .
.
Вычислим шаг разбиения: 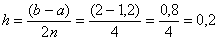 .
.
Заполним расчетную таблицу:  .
.
Таким образом : 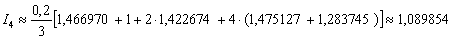 .
.
Оцениваем погрешность: 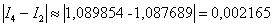 . Погрешность больше требуемой точности:
. Погрешность больше требуемой точности: 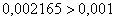 , поэтому необходимо еще раз удвоить количество отрезков:
, поэтому необходимо еще раз удвоить количество отрезков: 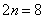 . Формула Симпсона растёт
. Формула Симпсона растёт 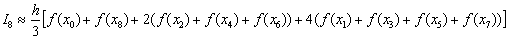 .
.
Вычислим шаг: 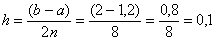 .
.
Заполним расчетную таблицу: 
Таким образом: 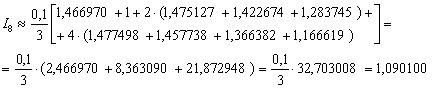
Вычисления желательно расписать более подробно, поскольку формула Симпсона достаточно громоздка: 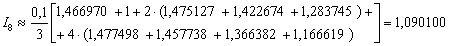 Оцениваем погрешность:
Оцениваем погрешность: 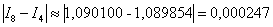 Погрешность меньше требуемой точности:
Погрешность меньше требуемой точности: 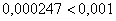 . Осталось взять наиболее точное приближение
. Осталось взять наиболее точное приближение 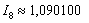 , округлить его до трёх знаков после запятой и записать: Ответ:
, округлить его до трёх знаков после запятой и записать: Ответ: 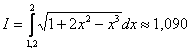 с точностью до 0,001.
с точностью до 0,001.
Пример 4. Вычислить приближенное значение определенного интеграла 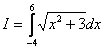 с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Точность вычислений 0,001.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Точность вычислений 0,001.
Решение: Результаты округлить до третьего знака после запятой, а не достигнуть такой точности. Используем формулу Симпсона: 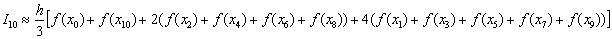 .
.
При десяти отрезках разбиения 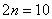 шаг составляет
шаг составляет 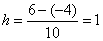 .
.
Заполним расчетную
таблицу: 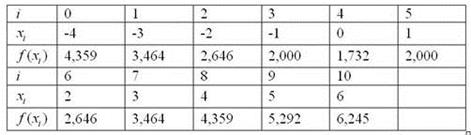 .
.
Таблицу рациональнее сделать двухэтажной. Вычисления расписываем подробнее:
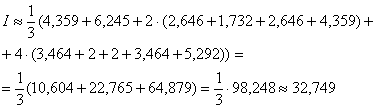 Ответ:
Ответ: 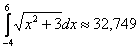 .
.
Ряды
. Числовой ряд – это выражение вида: a1 + a2 + . . . + an + . . .Числа а1, a2 …an. . . называются членами ряда. Они образуют бесконечную последовательность. Общий член ряда - это член anс производным номером. Сокращённо ряд обозначается: 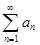 .Частичные суммы ряда – это суммы конечного числа членов рядаs1 = an, s2 = a1+a2, s3=a1+a2+a3, . . . sn = a1+a2+ . . . +аn.
.Частичные суммы ряда – это суммы конечного числа членов рядаs1 = an, s2 = a1+a2, s3=a1+a2+a3, . . . sn = a1+a2+ . . . +аn.
Сходящейся ряд – это ряд, у которого последовательность его частичных сумм имеет конечный предел при 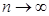 ;
; 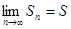 . Сумма ряда - это число s, к которому сходится последовательность частичных сумм:
. Сумма ряда - это число s, к которому сходится последовательность частичных сумм: 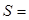
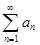 .Ряд называется расходящимся, если такой предел
.Ряд называется расходящимся, если такой предел 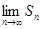 не существует или бесконечен. Алгоритм нахождения суммы ряда и его применение приводится в приложении 1.
не существует или бесконечен. Алгоритм нахождения суммы ряда и его применение приводится в приложении 1.
Необходимый признак сходимости. Если ряд 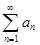
 сходится, то общий член ряда
сходится, то общий член ряда 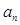 стремится к нулю при неограниченном возрастании n (при
стремится к нулю при неограниченном возрастании n (при 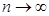 )
) 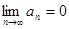 .Следствие. Если
.Следствие. Если 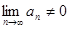 , то ряд
, то ряд 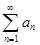 расходится.
расходится.
Пример 1. Исследовать на сходимость ряд 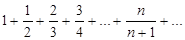
Решение: Найти 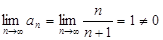 – предел отличен от нуля. Следовательно, данный ряд расходится. Ряд a + aq + aq2 + . . . +aqn-1 + . . ., составленной из бесконечной геометрической прогрессии со знаменателем q и первым членом a
– предел отличен от нуля. Следовательно, данный ряд расходится. Ряд a + aq + aq2 + . . . +aqn-1 + . . ., составленной из бесконечной геометрической прогрессии со знаменателем q и первым членом a  , называется геометрическим рядом. Если q>1, то геометрический ряд расходится, если
, называется геометрическим рядом. Если q>1, то геометрический ряд расходится, если 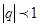 –сходится (при этом его сумма S находится по формуле
–сходится (при этом его сумма S находится по формуле 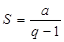 ).Ряд
).Ряд 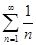 ,называется гармоническим. Гармонический ряд расходится.
,называется гармоническим. Гармонический ряд расходится.
Ряд 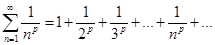 называется рядом Дирихле. Этот ряд сходится при
называется рядом Дирихле. Этот ряд сходится при 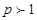 и расходится при
и расходится при 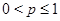
Признаки сходимости рядов с положительными членами.
Положительный ряд-это ряд, члены которого положительны.
Й признак сравнения
Пусть 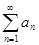 и
и 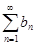 – ряды с положительными членами, причем
– ряды с положительными членами, причем 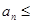
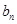 для всех номеров n, начиная с некоторого, тогда:
для всех номеров n, начиная с некоторого, тогда:
1)если ряд 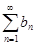 сходится, то сходится и ряд
сходится, то сходится и ряд 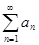 ;
;
2)если ряд 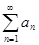 расходится, то расходится и ряд
расходится, то расходится и ряд 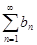
Й признак сравнения
Пусть 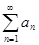 и
и 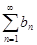 – ряды с положительными членами, причем существует конечный и отличный от нуля предел
– ряды с положительными членами, причем существует конечный и отличный от нуля предел 
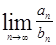 Тогда ряды
Тогда ряды 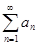 и
и 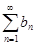 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
При использовании 1-ого или 2-ого признака сравнения, как правило, сравнивают исходные ряд с соответствующим рядом Дирихле. При этом часто используют эквивалентность следующих малых последовательностей
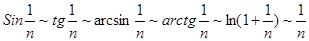 .
.
Пример 2. Исследовать сходимость ряда, применяя признак сравнения:
1) 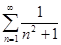 ;2)
;2) 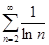
Решение:1) Находим 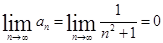 .Необходимый признак сходимости выполняется. Сравним данный ряд с обобщенным гармоническим рядом, рядом Дирихле
.Необходимый признак сходимости выполняется. Сравним данный ряд с обобщенным гармоническим рядом, рядом Дирихле 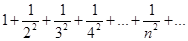 . Для всех
. Для всех 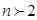 выполняется неравенство
выполняется неравенство 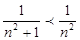 следовательно ряд сходится.
следовательно ряд сходится.
2) Для всех 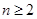 выполняется неравенство
выполняется неравенство 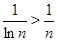 , следовательно ряд расходится.
, следовательно ряд расходится.
Признак Даламбера. Если для ряда с положительными членами 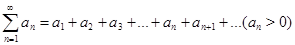 выполняется условие
выполняется условие 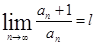 , то ряд сходится при l<1 и расходится при l>1.Признак Даламбера не дает ответа, если l=1 в этом случае для исследования ряда применяются другие методы.
, то ряд сходится при l<1 и расходится при l>1.Признак Даламбера не дает ответа, если l=1 в этом случае для исследования ряда применяются другие методы.
Пример 3. Исследовать на сходимость ряд:
1) 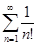 ; 2)
; 2) 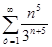 ; 3)
; 3) 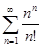 ;
;
Решение:
1) 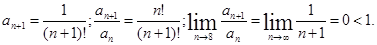 Ряд сходится.
Ряд сходится.
2) 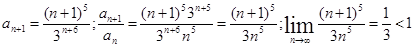 Ряд сходится.
Ряд сходится.
3) 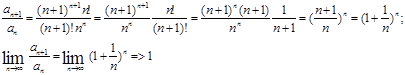 Ряд расходится.
Ряд расходится.
Признак Коши. Пусть 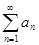 -ряд с положительными членами, и существует конечный предел
-ряд с положительными членами, и существует конечный предел 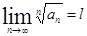 .Тогда, если l<1, то ряд сходится, если l>1, то ряд расходится. Если l=1,то ряд может сходится или расходится; в этом случае требуется исследовать ряд с помощью других методов.
.Тогда, если l<1, то ряд сходится, если l>1, то ряд расходится. Если l=1,то ряд может сходится или расходится; в этом случае требуется исследовать ряд с помощью других методов.
Пример 4. Исследовать на сходимость 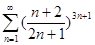
Решение: Учитывая, что 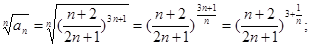
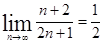
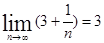 , получим
, получим 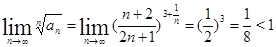 . Следовательно, ряд сходится по признаку Коши.
. Следовательно, ряд сходится по признаку Коши.
Знакопеременные ряды - это ряды, содержащие как положительные, так и отрицательные члены. Пусть дан знакопеременный ряд: 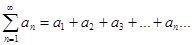
С каждым таким рядом связан ряд с неотрицательными членами, составленный из модулей членов данного ряда 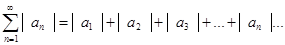
Теорема. Если ряд 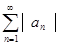 сходится, то сходится и ряд
сходится, то сходится и ряд 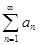 . Абсолютная сходимость: знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов.
. Абсолютная сходимость: знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов.
Условная сходимость: ряд 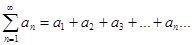 называется условно сходящимся, если он сходится, а ряд
называется условно сходящимся, если он сходится, а ряд 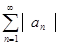 расходится. Знакочередующийся ряд-ряд, в котором любые два соседних члена имеют разные знаки, это ряд вида
расходится. Знакочередующийся ряд-ряд, в котором любые два соседних члена имеют разные знаки, это ряд вида 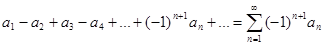 или
или
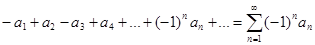
Признак Лейбница. Знакочередующийся ряд сходится, если выполнены два условия:
1) 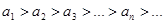 (абсолютные величины членов ряда монотонно убывают);
(абсолютные величины членов ряда монотонно убывают);
2) 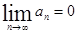 (общий член ряда стремится к нулю при ).
(общий член ряда стремится к нулю при ).
Пример 5.Пользуясь признаком Лейбница, исследовать на сходимость ряд: 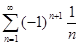
Решение: 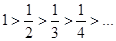 (абсолютные величины членов ряда монотонно убывают);
(абсолютные величины членов ряда монотонно убывают);
1) 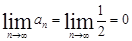 Ряд сходится.
Ряд сходится.
Пример 7.Исследовать на сходимость ряд 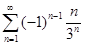
Решение: Исследуем на сходимость ряд, составленный из модулей членов данного ряда, т. е. ряд. 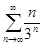 Используем признак Даламбера. Найдем отношение:
Используем признак Даламбера. Найдем отношение: 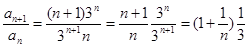 ,найдем предел этого отношения:
,найдем предел этого отношения: 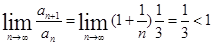 . Ряд, составленный из модулей, сходится, следовательно, исходный ряд сходится абсолютно.
. Ряд, составленный из модулей, сходится, следовательно, исходный ряд сходится абсолютно.
Функциональный ряд – это выражение вида 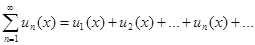
Где 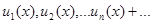 – некоторая последовательность функций. Функциональный ряд называется сходящимся в точке
– некоторая последовательность функций. Функциональный ряд называется сходящимся в точке 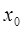 , если при x=
, если при x= 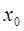 он обращается в сходящийся числовой ряд. Область сходимости функционального ряда – это совокупность всех значений, при которых ряд сходится. Из всех функциональных рядов наиболее распространенными на практике являются степенные ряды.
он обращается в сходящийся числовой ряд. Область сходимости функционального ряда – это совокупность всех значений, при которых ряд сходится. Из всех функциональных рядов наиболее распространенными на практике являются степенные ряды.
Степенным рядом называется ряд вида 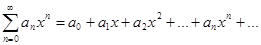 где числа
где числа 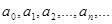 называются коэффициентом ряда, а член
называются коэффициентом ряда, а член 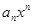 – общим членом ряда.
– общим членом ряда.
Число R называется радиусом сходимости ряда, если при 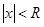 ряд сходится и при том абсолютно, а при
ряд сходится и при том абсолютно, а при 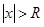 ряд расходится. Радиус сходимости R можно найти, используя признак Даламбера:
ряд расходится. Радиус сходимости R можно найти, используя признак Даламбера: 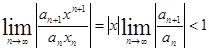 (x не зависит от n), откуда
(x не зависит от n), откуда 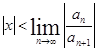 т.е. ряд сходится при любых x, удовлетворяющих этому условию, и расходится при
т.е. ряд сходится при любых x, удовлетворяющих этому условию, и расходится при 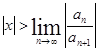 . Отсюда следует, что если существует предел R=
. Отсюда следует, что если существует предел R= 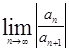 . То радиус сходимости ряда R равен этому пределу и ряд сходится при x < R, т. е. в промежутке – R < x < R, который называется интервалом сходимости. Если предел равен нулю (R = 0), то ряд сходится в единственной точке x = 0. Сходимость ряда при x = - R и x = R исследуется с помощью какого-либо из признаков сходимости.
. То радиус сходимости ряда R равен этому пределу и ряд сходится при x < R, т. е. в промежутке – R < x < R, который называется интервалом сходимости. Если предел равен нулю (R = 0), то ряд сходится в единственной точке x = 0. Сходимость ряда при x = - R и x = R исследуется с помощью какого-либо из признаков сходимости.
Пример8. Найти промежуток сходимости степенного ряда:
1) 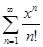 ; 2)
; 2) 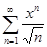
Решение: 1) Запишем коэффициент ряда 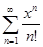 ;
; 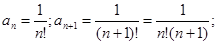
найдем отношение 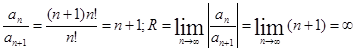 . Следовательно, промежуток сходимости есть -
. Следовательно, промежуток сходимости есть - 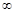 < x <
< x < 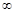 , т.е. данный ряд сходится на всей числовой прямой.
, т.е. данный ряд сходится на всей числовой прямой.
2)Запишем коэффициент ряда 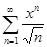
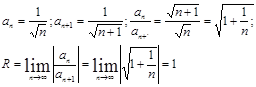 Следовательно, данный ряд сходится при -1 < x < 1. Исследуем сходимость ряда в точках x = -1 и x = 1При x=-1 имеем ряд
Следовательно, данный ряд сходится при -1 < x < 1. Исследуем сходимость ряда в точках x = -1 и x = 1При x=-1 имеем ряд 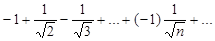 . Это знакочередующийся ряд, по признаку Лейбница сходится. При x=1имеет ряд
. Это знакочередующийся ряд, по признаку Лейбница сходится. При x=1имеет ряд 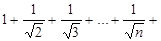 или
или 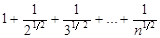 . Этот ряд Дирихле, который расходится, так как
. Этот ряд Дирихле, который расходится, так как 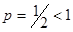 .Отсюда следует, что данный ряд сходится при -1
.Отсюда следует, что данный ряд сходится при -1 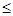 x<1.
x<1.
Разложение функций в степенные ряды.
Рядом Тейлора для функции называется степенной ряд вида
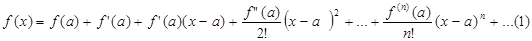
Если a=0, то получим частный случай ряда Тейлора
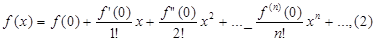 , который называется рядом Маклорена.
, который называется рядом Маклорена.
Для разложения функции в ряд Маклорена необходимо:
1)вычислить значения функции и её производных в точке x=0, т.е. f(0),f’(0),f”(0),… 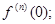
2)составить ряд Маклорена, подставив значения функции и ее последовательных производных в формулу 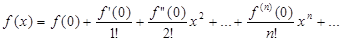
3)найти промежуток сходимости полученного ряда по формуле 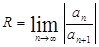
Пример 9.Разложить в ряд Маклорена функцию: 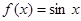
Решение: Вычислим значение функции и ее производных при x=0;
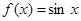
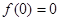
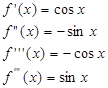
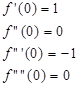 Заметим, что производные четного порядка
Заметим, что производные четного порядка 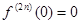 , а производные нечетного порядка
, а производные нечетного порядка 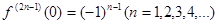 .Подставив эти значения в формулу (2), получим разложение синуса в ряд Маклорена:
.Подставив эти значения в формулу (2), получим разложение синуса в ряд Маклорена:
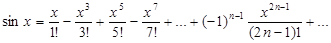 Определим промежуток сходимости полученного ряда
Определим промежуток сходимости полученного ряда
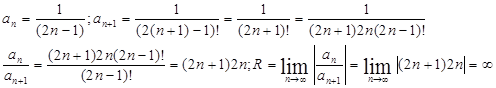
т.е. ряд сходится в промежутке 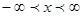 .
.
Сумма ряда. Основные понятия и определения.. Сумма ряда 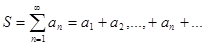 или
или 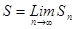 , где
, где 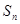 -частичные суммы.
-частичные суммы. 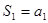 ,
, 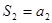 …,
…, 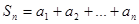
Найдите сумму ряда: 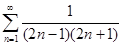 ;
; 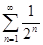
| План решения | Применение плана | |
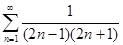
| 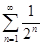
| |
1. Записать 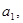 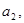 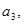 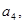 … …
| 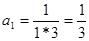 , , 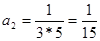 , ,
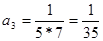 , , 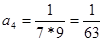
| 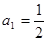 , , 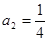 , , 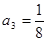 , ,
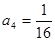 , , 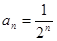 бесконечно убывающая прогрессия бесконечно убывающая прогрессия
|
2. Найти 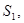 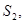 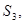 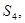
| 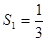 , , 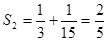 , , 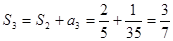 , , 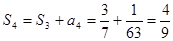 ,…, ,…,
| 
|
| 3.Записать последовательность частичных сумм. | 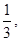 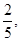 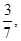 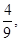
| |
| 4. Записать общий член последовательности | 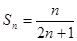 
| |
5. Найти 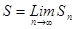
| 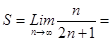 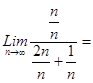 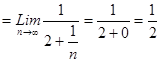
| Используя формулу 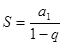 , получим , получим 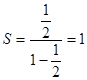
|
| 6. Сделать вывод | Ряд сходится и его сумма равна 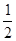
| Ряд сходится и его сумма равна 1 |
Признак Даламбера.
Если для ряда с положительными членами 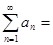
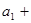
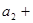
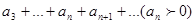 выполняется условие
выполняется условие 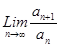 =
= 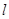 , тогда:
, тогда:
1)ряд сходимости при 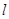 <1 2)ряд расходится при
<1 2)ряд расходится при 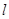 >1
>1
Исследовать сходимость ряда, используя признак Даламбера:
1) 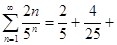
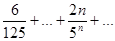 2)
2) 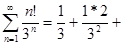
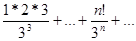
|
из
5.00
|
Обсуждение в статье: Методы интегрирования. Метод прямоугольников. Метод трапеции. Метод Симпсона. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы
(0.013 сек.)

