 |
Главная |
Изображение комплексных чисел радиус-векторами координатной плоскости
|
из
5.00
|
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
Назовем рассматриваемую плоскость комплексной плоскостью, и будем представлять комплексное число z = x + i y радиус–вектором с координатами (x , y).
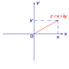 рис 1.
рис 1.
Назовем ось абсцисс Ox вещественной осью, а ось ординат Oy- мнимой осью.
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
Аргумент комплексного числа
Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа z.
Аргументом комплексногочисла z называют угол φмежду положительным направлением вещественной оси и радиус-вектором z.
Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным - в случае поворота по часовой стрелке (см. рис.2).
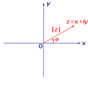 Рис.2
Рис.2
Считается, что комплексное число нуль аргумента не имеет.
Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k - произвольное целое число, то вводится, главное значение аргумента, обозначаемое arg z и удовлетворяющее неравенствам:
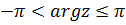
Тогда оказывается справедливым равенство: 
Если для комплексного числа z = x + i y нам известны его модуль r = | z | и его аргумент φ, то мы можем найти вещественную и мнимую части по формулам
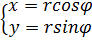
| (3) |
Если же комплексное число z = x + i y задано в алгебраической форме, т.е. нам известны числа x и y, то модуль этого числа, конечно же, определяется по формуле
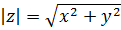
| (4) |
Тригонометрическая форма записи комплексного числа
Из формулы (3) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
| z = r (cos φ + i sin φ) , | (5) |
где r и φ - модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0.
Запись комплексного числа в форме (5) называют тригонометрической формой записи комплексного числа.
Пример 1. Записать в тригонометрической форме комплексное число z = 1+ i
Решение:
Модуль этого комплексного числа есть 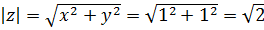 , тогда
, тогда 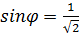 ,
, 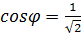 , откуда
, откуда 
Окончательно запишем:
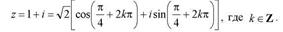
Обычно из бесконечного множества значений аргумента комплексного числа выбирают то, которое заключено между 0 и 2 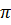 . В нашем случае таким значением является
. В нашем случае таким значением является  . Окончательно (рис. 3) запишем
. Окончательно (рис. 3) запишем 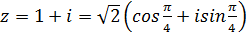

|
из
5.00
|
Обсуждение в статье: Изображение комплексных чисел радиус-векторами координатной плоскости |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

