 |
Главная |
Задачи для аудиторных занятий.
|
из
5.00
|
№ 2.1 Даны элементы A, B, C, D, E. Сколько можно составить перестановок, размещений (без повторений) и сочетаний из пяти по три?
№ 2.2 Сколько существует четырехзначных чисел, состоящих из цифр 2, 3, 6, 8, если каждая цифра входит в изображение числа только один раз?
№ 2.3 Брошены три игральные кости. Чему равно общее число исходов испытания?
№ 2.4 Сколько можно передать сигналов с помощью флажков различного цвета, взятых по 2?
№ 2.5 В торговом зале работает 8 продавцов-консультантов. Сколькими способами они могут распределить между собой обязанности кассира, упаковщика подарков и дежурного по залу?
№ 2.6 Из восьми продавцов-консультантов нужно выбрать трех упаковщиков подарков. Сколько возможно вариантов выбора?
№ 2.7 Сколькими способами можно распределить 8 человек в двух четырехместных купе?
№ 2.8 Сколько существует трехзначных чисел без повторяющихся цифр?
№ 2.9 Сколько существует пятизначных чисел, в записи 0; 1; 2; 3; 4 (возможны повторения)?
Задачи для самостоятельного решения.
№ 2.10 Брошены две игральные кости. Чему равно число возможных исходов испытания?
№ 2.11 Из пункта А в пункт С можно добраться только через пункт В. Из А в В ведет 4 пути, из В в С – 6 путей. Сколько путей ведет из А в С?
№ 2.12 Сколькими способами трехтомник стихотворений может быть расположен на книжной полке?
№ 2.13 В президиум собрания избраны 5 человек. Из их числа необходимо выбрать председателя и секретаря. Сколько возможно вариантов?
№ 2.14 В ящике 10 деталей одного вида. Сколькими способами можно выбрать две детали из ящика?
№ 2.15 Сколько пятизначных чисел можно записать цифрами 0; 1; 2; 3; 4; 5 без повторений?
№ 2.16 Сколько четырехзначных чисел можно составить, если все цифры в числе разные?
§3. Классический подход к определению вероятности. Элементы комбинаторики.
Теория и примеры.
Шанс появления случайного события оценивается численной величиной – вероятностью события. Существует несколько определений этого понятия.
Если элементарные исходы испытания несовместны, равновозможны и образуют полную группу, то пространство элементарных исходов является конечным. В этом случае справедливо классическое определение вероятности.
Вероятностью события А называют отношение числа m исходов, благоприятствующих появлению этого события, к числу n всех возможных элементарных исходов испытания:
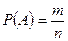 .
.
Замечание 1.
Достоинство классического определения вероятности заключается в том, что не требуется в действительности проводить испытание. Достаточно теоретически проанализировать все возможные исходы одного испытания.
Вероятность случайного события есть положительное число, заключенное между нулем и единицей (поскольку 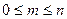 ):
):
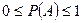 .
.
Вероятность достоверного события равна единице (поскольку m=n):
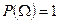 .
.
Вероятность невозможного события равна нулю (поскольку m=0).
Пример 1.
Проводится двукратное подбрасывание монеты. Определить вероятность того, что герб выпадет только один раз.
Решение.
Данная задача удовлетворяет условиям классического определения вероятностей.
Обозначим А – событие, состоящее в появлении герба один раз.
Перечислим возможные исходы опыта:
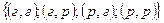 ,
,
где 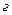 - выпадение герба,
- выпадение герба, 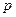 - выпадение решки,
- выпадение решки, 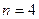 .
.
Событию А благоприятны исходы:
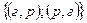 .
.
Следовательно, 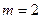 .
.
Искомая вероятность равна:
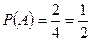 .
.
Пример 3.
В коробке 12 деталей, причём 8 из них стандартные. Наудачу извлечены 3 детали. Найти вероятность следующих событий: 1) А – все три стандартные; 2) В – только две стандартные; 3) хотя бы одна стандартная.
Решение.
Перенумеруем все детали:
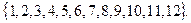
Пространство элементарных событий Ω состоит из всевозможных наборов из 12 деталей по 3:
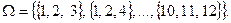
Общее число n элементарных исходов равно числу сочетаний из 12 по 3:
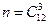 .
.
Так как это число конечно и все исходы равновероятны, то имеет место классическая схема определения вероятности.
1. Определим вероятность события А.
Число исходов, благоприятных событию А, равно числу способов, которыми можно три детали извлечь из восьми стандартных, то есть равно числу сочетаний 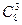 . Следовательно,
. Следовательно,
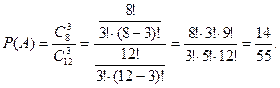
2. Определим вероятность события В.
Событие В заключается в том, что из трех извлеченных деталей две являются стандартными, следовательно, третья деталь должна быть нестандартной. Две детали можно извлечь из восьми стандартных 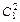 способами, а нестандартную третью можно извлечь из четырёх нестандартных деталей
способами, а нестандартную третью можно извлечь из четырёх нестандартных деталей 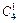 способами. По правилу произведения заключаем: число элементарных исходов, благоприятных событию В, равно
способами. По правилу произведения заключаем: число элементарных исходов, благоприятных событию В, равно 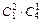 , поэтому
, поэтому
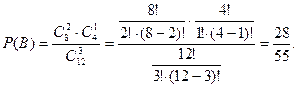
3. Определим вероятность события С.
Вероятность события С удобно находить так: 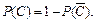 где
где 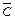 – событие, противоположное событию С, заключается в том, что все три извлеченные детали являются нестандартными.
– событие, противоположное событию С, заключается в том, что все три извлеченные детали являются нестандартными.
Число исходов, благоприятных событию 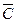 , равно числу способов, которыми можно три детали извлечь из четырех нестандартных, то есть равно числу сочетаний из 4 по 3 (
, равно числу способов, которыми можно три детали извлечь из четырех нестандартных, то есть равно числу сочетаний из 4 по 3 ( 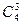 ), следовательно,
), следовательно,
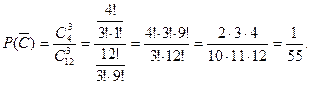
Тогда вероятность события С равна
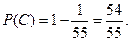
|
из
5.00
|
Обсуждение в статье: Задачи для аудиторных занятий. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

