 |
Главная |
Теорема сложения вероятностей.
|
из
5.00
|
Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
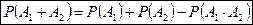
Если события А1 и А2 несовместны ( то есть 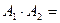 Ø, следовательно,
Ø, следовательно, 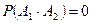 ), то вероятность суммы этих событий равна их вероятностей:
), то вероятность суммы этих событий равна их вероятностей:
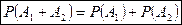
Теорему можно обобщить на случай любого конечного числа слагаемых. Так, для трех событий:
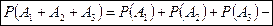
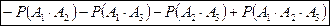 Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
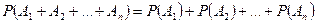 .
.
Сумма вероятностей событий 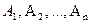 , образующих полную группу, равна 1, так как появление одного из событий полной группы достоверно:
, образующих полную группу, равна 1, так как появление одного из событий полной группы достоверно:
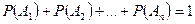 .
.
Сумма вероятностей противоположных событий равна 1, так как противоположные события образуют полную группу:
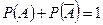 .
.
Часто обозначают 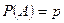 ,
, 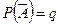 , тогда
, тогда 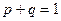 .
.
Замечание 1.
При решении задач на отыскание вероятности события А бывает выгодно сначала вычислить вероятность события 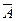 , а затем искомую вероятность:
, а затем искомую вероятность:
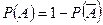 .
.
Два события могут находиться между собой в таких взаимоотношениях, что наступление или не наступление одного из них влияет на вероятность наступления второго. В таких случаях говорят, что события являются зависимыми.
Два события называются независимыми в данном испытании, если вероятность одного из них не зависит от того, появилось или не появилось другое событие.
Вероятность события B, вычисленная в предположении, что произошло событие А, называется условной вероятностью и обозначается 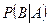 или
или 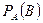 .
.
Если событие не зависит от события А, то 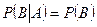 .
.
Если событие В зависит от события А, то 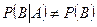 .
.
Теоремы умножения вероятностей.
Вероятность совместного наступления двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что произошло первое событие:
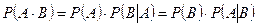
Теорему можно обобщить на случай любого конечного числа множителей.
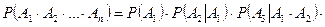
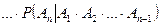 .
.
Если события A и В независимы, то 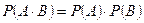 , так как
, так как 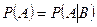 и
и 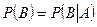 .
.
События 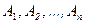 называются независимыми в совокупности, если каждое из них не зависит от появления любой комбинации остальных событий.
называются независимыми в совокупности, если каждое из них не зависит от появления любой комбинации остальных событий.
События 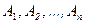 независимыми в совокупности, то вероятность их совместного появления вычисляется по формуле:
независимыми в совокупности, то вероятность их совместного появления вычисляется по формуле:
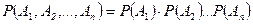 .
.
Вероятность произведения зависимых событий 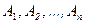 вычисляется по формуле:
вычисляется по формуле:
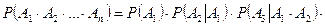
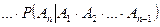
Вероятность появления хотя бы одного события из совокупности 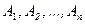 вычисляется по формуле
вычисляется по формуле
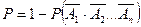 .
.
Пример 1.
На грузовой двор подают крытые двухосные и крытые четырехосные вагоны, а также полувагоны с вероятностями соответственно 0,25; 0,4; 0,35. Определить вероятность того, что очередным подадут крытый вагон.
Решение.
Подача крытого вагона означает подачу двухосного (событие А) или четырехосного (событие В) вагона. Эти события несовместны (так как вагоны подают по одному), поэтому применима теорема сложения вероятностей для несовместных событий:
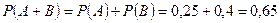 .
.
Пример 2.
Из колоды в 36 карт наугад достают одну карту. Определить вероятность того, что этой картой окажется какая-то из четырех дам или карта черной масти.
Решение.
Обозначим А – событие, состоящее в том, что вынутой картой окажется дама; В – событие, состоящее в том, что из колоды извлекли карту черной масти. Тогда 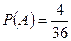 ;
; 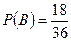 .
.
Заметим, что А и В – совместные случайные события. Извлеченной из колоды картой может оказаться, например, дама треф, и тогда произойдет и событие А, и событие В. Аналогичная ситуация для пиковой дамы. Поэтому 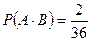 .
.
В данном случае вероятность суммы двух событий вычисляется по общей формуле:
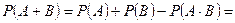
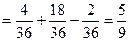 .
.
Пример 3.
В первом ящике 2 белых и 10 черных шаров, во втором – 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Какова вероятность того, что оба шара белые?
Решение.
Пусть А – появление белого шара из первого шара; В – появление белого шара из второго ящика.
Шанс вынуть белый шар из второго ящика не зависит от появления или не появления белого шара из первого ящика, следовательно, события А и В – независимые.
В каждом ящике по 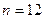 шаров, но количество белых шаров разное:
шаров, но количество белых шаров разное: 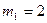 ;
; 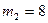 , поэтому
, поэтому
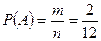 ;
; 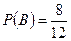 .
.
Пример 4.
В корзине 4 синих и 3 красных шара. Два раза подряд наудачу вынимают шар (без возвращения в корзину). Найти вероятности следующих событий:
1) второй шар синий, если первый был красным;
2) второй шар синий, если первый был синим;
3) вынули два синих шара;
4) вынули два шара одного цвета;
5) вынули два шара разного цвета.
Решение.
Обозначим события:
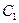 - первый раз вынули синий шар;
- первый раз вынули синий шар;
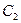 - второй раз вынули синий шар;
- второй раз вынули синий шар;
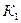 - первый раз вынули красный шар;
- первый раз вынули красный шар;
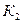 - второй раз вынули красный шар.
- второй раз вынули красный шар.
Вычислим искомые вероятности.
1) Всего шаров 7, из них 4 синих и 3 красных. Если первый раз вынули красный шар, то осталось 6 шаров, из них 4 синих и 2 красных.
Следовательно, вероятность того, что вторым вынули синий шар, если первым был красный шар – это вероятность события 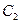 при условии, что событие
при условии, что событие 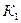 уже произошло, и является условной вероятностью:
уже произошло, и является условной вероятностью:
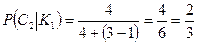 .
.
2) Если первым вынули синий шар, то произошло событие 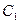 . При этом уменьшилось общее количество шаров (стало 6) и количество синих шаров (стало 3). Вероятность вынуть вторым синий шар при условии, что первым был также синий шар, равна:
. При этом уменьшилось общее количество шаров (стало 6) и количество синих шаров (стало 3). Вероятность вынуть вторым синий шар при условии, что первым был также синий шар, равна:
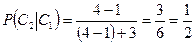 .
.
3) Вынуть два синих шара подряд означает совмещение событий 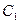 и
и 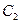 :
: 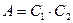 . Эти события зависимы. В п. 1 и п. 2 показано, что вероятность события
. Эти события зависимы. В п. 1 и п. 2 показано, что вероятность события 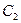 зависит от того, какое событие ему предшествовало.
зависит от того, какое событие ему предшествовало.
Вероятность появления двух синих шаров (т. е. вероятность события А) найдем по теореме умножения вероятностей для зависимых событий:
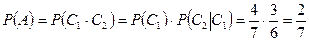 .
.
4) Вынуть два шара одного цвета (событие F) означает появление двух синих шаров (событие 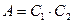 ) или появлении двух красных шаров (событие
) или появлении двух красных шаров (событие 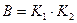 ). События А и В несовместны: появление одного из них исключает появление другого.
). События А и В несовместны: появление одного из них исключает появление другого.
Вероятность появления двух шаров одного цвета определим по теореме сложения вероятностей:
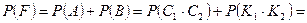
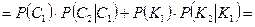
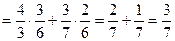 .
.
5) Вынуть шары разного цвета (событие R) означает вынуть первый шар синий, а второй – красный (событие 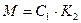 ) или вынуть первый шар кранный, а второй синий (событие
) или вынуть первый шар кранный, а второй синий (событие 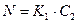 ). События M и N несовместны. По теореме сложения вероятностей:
). События M и N несовместны. По теореме сложения вероятностей:
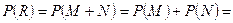
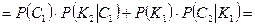
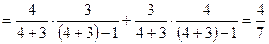 .
.
Пример 5.
Два баскетболиста делают независимо друг от друга по одному броску в корзину. Вероятность попадания для 1-го баскетболиста 0,8, для 2-го баскетболиста 0,7. Найти вероятности следующих событий:
1) А – 1-й попал, 2-й не попал;
2) В – только один попал;
3) С – ни один не попал;
4) D – хотя бы один попал.
Решение.
Введем события, вероятности которых известны по условию задачи:
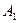 – 1–й баскетболист попал в корзину,
– 1–й баскетболист попал в корзину,
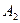 – 2-й баскетболист попал в корзину.
– 2-й баскетболист попал в корзину.
Тогда 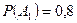 ,
, 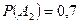 ,
, 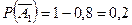 ,
, 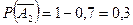 .
.
1) Выразим событие 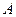 через
через 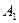 и
и 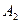 :
:
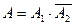 .
.
Так как события 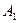 и
и 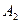 (следовательно, и события
(следовательно, и события 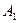 и
и 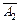 ) являются независимыми, то
) являются независимыми, то
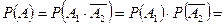
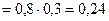 .
.
2) Выразим события В через 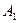 и
и 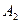 . Событие
. Событие 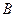 заключается в том, что 1-й баскетболист попал в корзину, а 2-й не попал (событие
заключается в том, что 1-й баскетболист попал в корзину, а 2-й не попал (событие 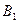 ), или 2-й баскетболист попал в корзину, а 1-й не попал (событие
), или 2-й баскетболист попал в корзину, а 1-й не попал (событие 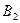 , поэтому
, поэтому
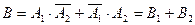 .
.
События 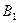 и
и 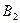 являются несовместными, следовательно,
являются несовместными, следовательно,
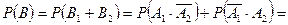
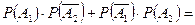
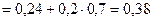 .
.
3) Выразим событие 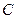 через
через 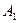 и
и 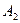 .
.
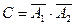 .
.
В силу независимости событий 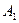 и
и 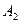 (следовательно, и событий
(следовательно, и событий 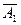 и
и 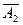 заключаем:
заключаем:
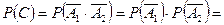
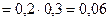 .
.
4) Событие 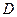 представляет собой сумму событий
представляет собой сумму событий 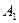 и
и 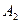 :
:
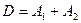 .
.
По теореме сложения вероятностей, учитывая, что 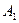 и
и 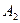 являются независимыми, получаем:
являются независимыми, получаем:
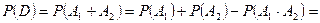
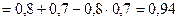 .
.
Вероятность события 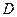 можно находить иначе.
можно находить иначе.
Событие 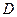 - попал хотя бы один, подразумевает, что 1-й попал, 2-й промахнулся (событие
- попал хотя бы один, подразумевает, что 1-й попал, 2-й промахнулся (событие 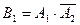 ), или 1-й промахнулся, 2-й попал (событие
), или 1-й промахнулся, 2-й попал (событие 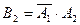 , или оба попали (событие
, или оба попали (событие 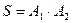 ). События
). События 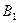 ,
, 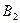 и
и 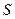 несовместны.
несовместны.
Искомая вероятность определяется по теореме сложения вероятностей:
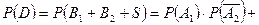
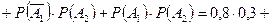
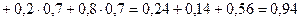 .
.
Еще один способ определения 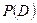 основан на том, что события
основан на том, что события 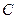 и
и 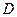 являются противоположными:
являются противоположными: 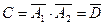 . Поэтому
. Поэтому
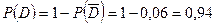 .
.
Пример 6.
В коробке 12 деталей, причём 8 из них стандартные. Наудачу извлечены 3 детали. Найти вероятность события А – все три извлеченные детали являются стандартными.
Решение.
Данная задача уже была рассмотрена при изучении темы «Классический подход к определению вероятности» (см. пример 3).
Рассмотрим другой способ решения этой задачи.
Введем события:
А1 – первый раз извлечена стандартная деталь;
А2 – второй раз извлечена стандартная деталь;
А3 – третий раз извлечена стандартная деталь.
Тогда событие А произойдет, если произойдут все три события А1, А2 и А3, то есть
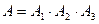 .
.
По теореме умножения вероятностей
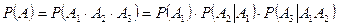 .
.
Так как всего 12 деталей, и из них 8 стандартные, то
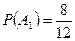 .
.
После извлечения одной стандартной детали останется 11 деталей, из которых 7 деталей стандартные, следовательно,
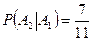 .
.
После извлечения стандартной детали во второй раз, останется 10 деталей, среди которых 6 стандартных, поэтому
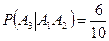
Таким образом,
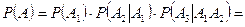
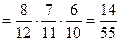 .
.
|
из
5.00
|
Обсуждение в статье: Теорема сложения вероятностей. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

