 |
Главная |
Локальная приближенная формула
|
из
5.00
|
Муавра-Лапласа:
 , где
, где
 ,
, 
Обычно этой формулой пользуются в случае, если  (n достаточно велико, р по-прежнему отлично от 0 и 1). Найденное значение
(n достаточно велико, р по-прежнему отлично от 0 и 1). Найденное значение  тем точнее n.
тем точнее n.
Замечание 1. Функцию 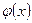 можно находить по специальным таблицам (см. Приложение 1), где помещены значения функции
можно находить по специальным таблицам (см. Приложение 1), где помещены значения функции 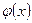 для неотрицательных х. Значения функции
для неотрицательных х. Значения функции  для отрицательных х легко найти, обратив внимание на то, что
для отрицательных х легко найти, обратив внимание на то, что  является четной функцией:
является четной функцией:  .
.
Интегральная приближенная формула
Муавра-Лапласа:
 , где
, где
 ,
, 
Таким образом, интегральная приближенная формула Муавра-Лапласа позволяет находить вероятность того, что в n испытаниях число наступлений некоторого события находится между k1 и k2 при условии, что n велико;  .
.
Замечание 2. Функцию 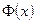 также можно находить по специальным таблицам (см. Приложение 2), где помещены значения функции
также можно находить по специальным таблицам (см. Приложение 2), где помещены значения функции  для неотрицательных х. Значения функции
для неотрицательных х. Значения функции  для отрицательных х легко найти, обратив внимание на то, что
для отрицательных х легко найти, обратив внимание на то, что 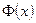 является нечетной функцией:
является нечетной функцией:  . При
. При 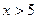 можно принять
можно принять  .
.
Приближенная формула Пуассона:
 , где
, где 
Формулой Пуассона пользуются при анализе массовых (n велико), редких  событий, если можно допустить, что среднее число
событий, если можно допустить, что среднее число 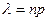 появлений события в различных сериях испытаний остается неизменным.
появлений события в различных сериях испытаний остается неизменным.
Пример 1.
Стрелок делает 4 независимых выстрела по мишени, в каждом из которых вероятность попадания равна 0,8. Найти вероятности следующих событий:
В – стрелок попал в мишень один раз,
С – стрелок попал в мишень два раза.
Решение.
Введем события А i – стрелок попал в мишень при i-том выстреле, где  .
.
По условию  , следовательно,
, следовательно, 
Выразим через события В и С через А i :
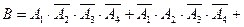
 ;
;
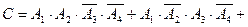

 .
.
Видим, что события В и С, состоят из ряда сложных несовместных событий, каждое из которых представляет собой произведение независимых элементарных событий  и
и 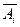 .
.
Найдем вероятности событий В и С:


 .
.



 .
.
Замечание 3.
При вычислении вероятности события В получены одинаковые слагаемые: в каждом из них присутствует 0,8. Это показывает, что в одном из четырех испытаний произошли события А i, вероятности которых постоянны и равны 0,8. Присутствие (0,2)3 показывает, что в оставшихся трех испытаниях произошли события  . Всего таких слагаемых 4, что равно числу способов, которыми можно из четырех испытаний выбрать одно, в котором произойдет событие А i, то есть равно числу сочетаний из четырех по одному (
. Всего таких слагаемых 4, что равно числу способов, которыми можно из четырех испытаний выбрать одно, в котором произойдет событие А i, то есть равно числу сочетаний из четырех по одному (  ).
).
Аналогично при вычислении вероятности события С получили одинаковые слагаемые: в каждом из них присутствует (0,8)2 (это показывает, что в двух из четырех испытаний произошли событие Аi), и (0,2)2, (это показывает, что в оставшихся двух испытаниях произошли события  ). Всего таких слагаемых 6, что равно числу способов, которыми можно из четырех испытаний выбрать два, в которых произойдет событие
). Всего таких слагаемых 6, что равно числу способов, которыми можно из четырех испытаний выбрать два, в которых произойдет событие
А i, то есть равно числу сочетаний из четырех по два (  ).
).
С учетом Замечания вероятности событий В и С могут быть найдены гораздо быстрее, если применить формулы Бернулли:
 ;
;

Пример 2.
Вероятность некоторого события в каждом испытании постоянна и равна 0,75. Найти вероятность того, что это событие в 192 испытаниях наступит 1) 150 раз, 2) 135 раз, 3) не менее 135 и не более 150 раз.
Решение:
По условию  ,
,  . Величина
. Величина  .
.
Воспользуемся приближенными формулами Муавра-Лапласа.
1) Найдем х и по таблице  для
для  :
:
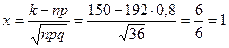
 .
.
Тогда  .
.
2) Найдем х и по таблице  для
для  :
:

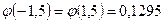 .
.
Тогда  .
.
1) По таблице находим:
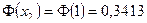 ,
,  .
.

 .
.
|
из
5.00
|
Обсуждение в статье: Локальная приближенная формула |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

