 |
Главная |
Проверка адекватности модели
|
из
5.00
|
Одним из важных этапов идентификации объектов автоматизации является проверка качества модели по выбранному критерию близости выхода модели и объекта, т.е проверка ее адекватности. В пакете System Identification Toolbox MATLAB в качестве такого критерия принята оценка адекватности модели fit, которая рассчитывается по формуле: fit = norm (yh – y)/  , где norm – норма вектора; yh и y – выходы модели и объекта соответственно; N – количество элементов массива данных.
, где norm – норма вектора; yh и y – выходы модели и объекта соответственно; N – количество элементов массива данных.
Для проверки адекватности полученных ранее моделей воспользуемся функцией:
>> compare(zdane,zn4s,zpem,zoe,zbj,darx,darmax).
где: zdane – выход объекта;
 zn4s,zpem,zoe,zbj,darx,darmax – выходы моделей zn4s,zpem,zoe,zbj,darx,darmax
zn4s,zpem,zoe,zbj,darx,darmax – выходы моделей zn4s,zpem,zoe,zbj,darx,darmax

Рис. 2 . 11. Графики выходов объекта и моделей.
Результатом выполнения команды является вывод графика выходов объекта и построенных моделей (Рис. 2. 11). На графике цветными линиями представлены выходы полученных моделей и значения критерия адекватности, выраженного в процентах. Наилучшие показатели имеют модели darx, zn4s и zpem.
Для проверки адекватности модели zn4s воспользуемся функцией:
>>compare(zdane,zn4s)
Результат выполнения команды является вывод графика объекта на рис. 2. 12.
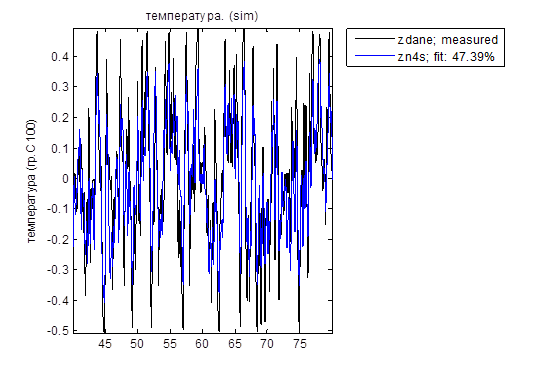
 Рис. 2 . 12. Графики выходов объекта и модели zn4s.
Рис. 2 . 12. Графики выходов объекта и модели zn4s.
В пакете System Identification Toolbox MATLAB имеется возможность прогнозировать ошибку моделирования при заданном входном воздействии u ( t ) и известной выходной координате объекта y ( t ). Оценивание производится методом прогноза ошибки Preictive Error Method, сокращенно PEM, который заключается в следующем. Пусть модель исследуемого объекта имеет вид так называемой обобщенной линейной модели
y(t) = W(z) u(t) + v(t),
где W(z) – дискретная передаточная функция любой из ранее рассмотренных моделей. При этом шум v(t) может быть представлен как
v(t) = H(z) e(t),
где e(z) – дискретный белый шум, который собственно и характеризует ошибку модели; H(z) – некоторый полином от z, приводящий дискретный белый шум к реальным помехам при измерении выходных параметров объекта.
Из данных выражений следует, что
e(t) = H-1(z) [y(t) – W(z) u(t)].
Функция resid вычисляет остаточную ошибку e для заданной модели, а также r – матрицу значений автокорреляционной функции процесса e(t) и значения взаимокорреляционой функции между остаточными ошибками e(t) и выходами объекта автоматизации y(t) вместе с соответствующими 99 %-ми доверительными коридорами. Кроме указанных значений выводятся графики данных функций. В качестве примера сравним остаточные ошибки и соответствующие корреляционные функции для полученных моделей darx и zbj, имеющих максимальную и минимальную оценки адекватности с помощью команд:
>> [e,r]=resid(zdan,darx)
>> [e1,r1]=resid(zdan,zbj)
Приведенные графики (рис. 2. 13 и 2 14) характеризуют равномерное распределение остаточных ошибок во всем диапазоне изменения интервалов времени τ. Причем значения остаточных ошибок  для модели darx практически в два раза больше, чем для модели zbj. Для вывода графиков необходимо выполнить команду resid(r).
для модели darx практически в два раза больше, чем для модели zbj. Для вывода графиков необходимо выполнить команду resid(r).

Рис. 2. 13. График автокорреляционной и взаимокорреляционной функций для модели zbj

Рис. 2 . 14. График автокорреляционной и взаимокорреляционной функций для модели darx
 После выполнения функции:
После выполнения функции:
[e,r]=resid(zdan,darx)
MATLAB возвращает:
Time domain data set with 1097 samples.
Sampling interval: 0.08
Outputs Unit (if specified)
e@температура гр.С 100
Inputs Unit (if specified)
u1
r =
1.0e+003 *
Columns 1 through 8
0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000 -0.0000
0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000
0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000
0.0002 0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000
Columns 9 through 16
-0.0000 -0.0000 0.0000 -0.0000 -0.0000 0.0000 -0.0000 -0.0000
-0.0000 -0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000
-0.0000 -0.0000 -0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000
 -0.0000 -0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000
-0.0000 -0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000
Columns 17 through 24
-0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000
-0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 -0.0000
0.0000 0.0000 -0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000
0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000
Columns 25 through 27
0.0000 1.0970 0.0010
-0.0000 0 0
0.0000 0 0
-0.0000 0 0
После выполнения команды >> resid(r) выводится график автокорреляционной и взаимокорреляционной функций для модели.
Таким образом, в ходе оценки адекватности различных моделей объекта автоматизации технологического процесса тепловой обработки материалов определены модели darx, zn4s и zpem, значения критерия адекватности которых максимальны и, следовательно, могут быть использованы в дальнейшем при анализе и синтезе систем автоматизации.
2. 11 . Анализ модели технического объекта управления
Для анализа модели ТОУ возьмем модель zn4s, имеющую один из наилучших показателей адекватности.
• zzn4s – дискретная модель в виде передаточной функции
0.1327 z^2 + 0.1566 z + 0.0575
------------------------------------
z^3 - 0.3799 z^2 - 0.281 z + 0.07493
• sysn4s – непрерывная модель в виде передаточной функции
-0.891 s^2 + 77.33 s + 746.9
---------------------------------
s^3 + 32.39 s^2 + 308.9 s + 891.7
Приведенные виды являются одной и той же моделью, записанной в разных формах и форматах. Проанализируем динамические характеристики модели. Построим переходную характеристику ТОУ для дискретной и непрерывной моделей и определим основные показатели переходного процесса. Для этого можно воспользоваться функцией step. Функция step рассчитывает и строит реакцию модели на единичную ступенчатую функцию, т. е. возвращает переходную функцию системы:
step(sys)
step(sys, t)
step(sys1,sys2,….,sysN, t)
step(sys1,’PlotStyle1’,….,sysN, ’PlotStyleN’)
[y,t,x] = step(sys)
Д  ля моделей, заданных в пространстве состояний, начальные условия принимаются нулевыми. Аргументы функции следующие:
ля моделей, заданных в пространстве состояний, начальные условия принимаются нулевыми. Аргументы функции следующие:
· sys,sys1,sys2,….,sysN – имена моделей для которых строятся переходные функции;
· t – аргумент, задающий момент окончания моделирования – либо в форме t = Tfinal (в секундах), либо в форме t = 0:dt:Tfinal.
Для дискретных моделей значение dt должно равняться интервалу дискретизации, для непрерывных моделей – быть достаточно малым, чтобы учесть наиболее быстрые изменения переходного процесса;
· ’PlotStyle1’,….,’PlotStyleN’ – строковые переменные, задающие стили (типы линий) при выводе нескольких графиков одновременно.
Возвращаемые величины:
· графики переходных процессов;
· y, x, t – соответственно, векторы, содержащие значения переходного процесса, переменных состояния и моментов времени (при возвращении данных величин график переходного процесса не отображается).
Выполним построение переходной характеристики ТОУ, представленной дискретной zzn4s инепрерывной sysn4s моделями и определим основные показатели переходного процесса, используя функцию step:
>>step(zzn4s,sysn4s)
После выполнения команды step MATLAB возвращает графики переходного процесса (Рис. 2. 15). Нажатие левой клавиши мыши в любом месте на графике переходного процесса приводит к появлению всплывающей информационной подсказки о величине текущего численного значения переходного процесса и моменте времени.
 Нажатие правой клавиши в любом месте на графике переходного процесса приводит к появлению всплывающего меню редакции окна всплывающей информационной подсказки.
Нажатие правой клавиши в любом месте на графике переходного процесса приводит к появлению всплывающего меню редакции окна всплывающей информационной подсказки.

 Рис. 2 . 15. Графики переходных процессов модели z zn4s и sy sn4s
Рис. 2 . 15. Графики переходных процессов модели z zn4s и sy sn4s
На графиках переходных процессов ступенчатой линией представлен переходной процесс дискретной модели, а сплошной линией – непрерывной модели. Кроме того, в поле графика указаны основные характеристики переходного процесса:
• время регулирования (Setting time) – 0,769 с для обоих моделей;
• установившееся значение выходной координаты – 0,838 для обеих моделей.
Для построения импульсной характеристики моделей необходимо воспользоваться командой:
>>impulse(zzn4s,sysn4s).
После выполнения команды impulse MATLAB возвращает графики (Рис. 2. 16).
Основными характеристиками модели ТОУ при подаче на вход единичного импульсного воздействия являются:
• пиковая амплитуда (Peak amplitude) составляет для дискретной модели 0,207 а для непрерывной – 2,79.
• время регулирования составляет для дискретной модели 0,922 и для непрерывной модели – 0,863 с.
Для определения статического коэффициента усиления модели ТОУ можно использовать команду dcgain :
>> k=dcgain(sysn4s)
После выполнения команды получим: k = 0.8376. 
Рис. 2 . 16. Графики импульсной характеристики
Для определения частотной характеристики моделей используем команду bode: 

Рис.2. 17. Частотные характеристики моделей
Выполним построение частотной характеристики ТОУ, представленной дискретной zzn4s и непрерывной sysn4s моделями (Рис. 2. 17).
Н  а графиках частотных характеристик указаны значения запасов устойчивости по амплитуде (Gain Margin), которые для дискретной модели составляет 29,7 dB, а для непрерывной модели – бесконечность.
а графиках частотных характеристик указаны значения запасов устойчивости по амплитуде (Gain Margin), которые для дискретной модели составляет 29,7 dB, а для непрерывной модели – бесконечность.
Значения запасов устойчивости можно определить также и в режиме командной строки MATLAB с помощью команд:
>> [Gm,Pm,Wcg,Wcp]=margin(sysn4s) – для непрерывной модели:
MATLAB возвращает:
Gm =
26.5077
Pm =
Inf
Wcg =
48.5667
Wcp =
NaN
>> [Gm1,Pm1,Wcg1,Wcp1]=margin(zzn4s) – для дискретной модели:
MATLAB возвращает:
Gm1 =
9.0385
Pm1 =
Inf
Wcg1 =
21.0461
Wcp1 =
NaN
где Gm – запас устойчивости по амплитуде в натуральных величинах на частоте Wcg, Pm – запас устойчивости по фазе на частоте Wcp.
Для определения запасов устойчивости в логарифмическом масштабе необходимо выполнить следующие операции:
>> Gmlog=20*log10(Gm1) – для дискретной модели:
Gmlog =
19.1219
>> Gmlog=20*log10(Gm) – для непрерывной модели:
Gmlog =
28.4675
Как видно, определение запасов устойчивости последним способом позволяет значительно точнее вычислять эти значения, чем на графиках частотных характеристик. Анализ частотных характеристик показывает, что модели zzn4s и sysn4s являются устойчивыми с соответствующими запасами устойчивости по амплитуде. Запас устойчивости по фазе равен бесконечности.
Этот вывод подтверждается так же комплексной амплитудно-фазовой характеристикой АФХ (называется диаграммой Найквиста, Рис. 2. 18), так как годограф АФХ не пресек  ает точку комплексной плоскости с координатами –1, j0.
ает точку комплексной плоскости с координатами –1, j0.
 Рис. 2 . 18. Годограф АФХ для непрерывной и дискретной моделей
Рис. 2 . 18. Годограф АФХ для непрерывной и дискретной моделей
Для построения АФХ необходимо воспользоваться командой:
>>nyquist(zzn4s,sysn4s),
Определить устойчивость моделей можно с помощью карты нулей и полюсов по расположению нулей моделей относительно окружности с единичным радиусом на комплексной плоскости, как это было показано на рис. 2. 10. Построить карту нулей и полюсов моделей можно так же с помощью команды pzmap(zzn4s,sysn4s), либо – pzmap(zn4s,sn4s).
Построим график изменения e(t) и определим основные статистические характеристики помехи с помощь команды plot (e) (Рис. 2. 19).
Для получения статистических характеристик необходимо в строке меню графика в позиции Tools выбрать опцию Data statistics. Результатом выполнения команды явится окно, в котором будут указаны основные статистические характеристики случайного процесса изменения во времени e(t),(Рис. 2. 20), к которым относятся:
• min и max – минимальное и максимальное значения помехи.
Для нашего случая – -0,2373 и 0,2086 соответственно;
• mean – арифметическое среднее значение (0,001403);
• median – медиана процесса (0,003994);
• std – среднеквадратическое отклонение (0,0805);
• range – диапазон изменения помехи от минимального до максимального значения (1.12).Во всех случаях размерность аддитивной помехи такая же, как и выходная величина объекта автоматизации – оС.

Рис. 5. 19. График аддитивной помехи e ( t )
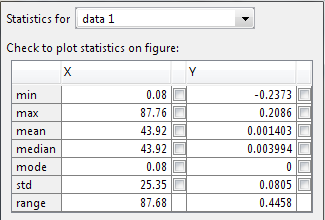
Рис. 5. 20. Статистические характеристики e ( t )
Полученные статистические характеристики помехи могут быть полезны в дальнейшем при синтезе системы автоматического регулирования температуры теплового объекта автоматизации.
 Для решения задач анализа и синтеза систем управления важно знать ответ на другой не менее важный вопрос, чем полученные временные, частотные и статистические характеристики: обладает ли объект свойством управляемости в смысле возможности его перевода из заданной начальной точки (или области) в заданную конечную точку (или область). Решение проблемы управляемости основано на анализе уравнений переменных состояния вида:
Для решения задач анализа и синтеза систем управления важно знать ответ на другой не менее важный вопрос, чем полученные временные, частотные и статистические характеристики: обладает ли объект свойством управляемости в смысле возможности его перевода из заданной начальной точки (или области) в заданную конечную точку (или область). Решение проблемы управляемости основано на анализе уравнений переменных состояния вида:
 ,
,
 ,
,
где A , B , C , D – матрицы соответствующих размеров, v(t) – коррелированный белый шум наблюдений. Возможна и другая (так называемая обновленная или каноническая) форма представления данной модели:
 ,
,
 ,
,
 где К – некоторая матрица (вектор столбец), е(t) – дискретный белый шум (скаляр),
где К – некоторая матрица (вектор столбец), е(t) – дискретный белый шум (скаляр),
и формулируется следующим образом: объект называется вполне управляемым, если выбором управляющего воздействия u(t) на интервале времени [t 0 , tk ] можно перевести его из любого начального состояния y ( t 0 ) в произвольное заранее заданное конечное состояние y ( tk ).
Критерием управляемости линейных стационарных объектов является условие: для того чтобы объект был вполне управляем, необходимо и достаточно, чтобы ранг матрицы управляемости
MU = (B AB A2B … An-1B)
равнялся размерности вектора состояний n
rang MU = n .
В пакете Control System Toolbox имеется функция ctrb, формирующая матрицу управляемости в пространстве состояний. Для того, чтобы воспользоваться этой функцией необходимо вычислить матрицы A, B, C, D с помощью команды:
>>[A,B,C,D]=ssdata(sn4s)
A =
-0.8930 16.3384 4.0253
-4.7215 -22.0535 -3.5128
-1.0484 -2.5116 -9.4429
B =
0.3680
-1.5178
-0.3597
C =
-4.6742 -0.5470 0.0028
D =
0
Следует обратить внимание, что для расчета матриц используется непрерывная модель, так как дискретная модель имеет другие значения, а в критерии управляемости используются матрицы линейных непрерывных стационарных объектов.
Вычислим матрицу управляемости:
>> Mu=ctrb(A,B)
Mu =
0.3680 -26.5754 590.3514
-1.5178 32.9991 -626.2378
-0.3597 6.8234 -119.4511
Определим ранг матрицы управляемости:
>> n=rank(Mu)
 n =
n =
3.
Таким образом, для исследуемой модели объекта размерность вектора состояний, определяемая размером матриц A и B равна трем и ранг матрицы управляемости MU также равен трем, что позволяет сделать вывод о том, что объект автоматизации является вполне управляемым, т.е. для него имеется такое управляющее воздействие u(t), которое способно перевести на интервале времени [t0, tk] объект из любого начального состояния y ( t 0 ) в произвольное заранее заданное конечное состояние y ( tk ).
При синтезе оптимальных систем с обратной связью сами управления получаются как функции от фазовых координат. В общем случае фазовые координаты являются абстрактными величинами и не могут быть исследованы. Поддается измерению (наблюдению) вектор y = (y 1, …, yk)T, который обычно называют выходным вектором или выходной переменной, а его координаты – выходными величинами. Выходная переменная функционально связана с фазовыми координатами, и для реализации управления с обратной связью необходимо определить фазовые координаты по измеренным значениям выходной переменной. В связи с этим возникает проблема наблюдаемости, заключающаяся в установлении возможности состояния определения состояния объекта (фазового вектора) по измеренным значениям выходной переменной на некотором интервале.
Решение проблемы наблюдаемости основано на анализе уравнений переменных состояния вида  или Y ( p ) = W ( p )* U ( p ) и формулируется следующим образом: объект называется вполне наблюдаемым, если по реакции y(t 1 ) на выходе объекта, на интервале времени [t0, t1] при заданном управляющем воздействии u(t) можно определить начальное состояние вектора переменных состояния x(t), являющихся фазовыми координатами объекта.
или Y ( p ) = W ( p )* U ( p ) и формулируется следующим образом: объект называется вполне наблюдаемым, если по реакции y(t 1 ) на выходе объекта, на интервале времени [t0, t1] при заданном управляющем воздействии u(t) можно определить начальное состояние вектора переменных состояния x(t), являющихся фазовыми координатами объекта.
Критерием наблюдаемости линейных стационарных объектов является
условие: для того, чтобы объект был вполне наблюдаемым, необходимо и достаточно, чтобы ранг матрицы наблюдаемости
 М Y = (CT ATCT (AT)2CT … ( AT ) n -1C )
М Y = (CT ATCT (AT)2CT … ( AT ) n -1C )
равнялся размерности вектора состояния
n = rang M Y.
Определим матрицу наблюдаемости и ее ранг с помощью функций пакета Control System Toolbox:
>> My=obsv(A,C)
My =
1.0e+003 *
-0.0047 -0.0005 0.0000
0.0068 -0.0643 -0.0169
0.3154 1.5712 0.4129
>> n=rank(My)
n =3
Таким образом, для исследуемой модели объекта размерность вектора состояний, определяемая размером матриц A и С равна трем и ранг матрицы наблюдаемости M Y также равен трем, что позволяет сделать вывод о том, что объект автоматизации является вполне наблюдаемым, т.е. для него всегда можно определить по значениям выходной величины y ( t ) вектор переменных состояния, необходимый для синтеза системы управления.
|
из
5.00
|
Обсуждение в статье: Проверка адекватности модели |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

