Функция многих переменных

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

 

Кафедра математического анализа

 

Дипломная работа по математике

студентка 5 курса математического факультета

специальность 032100.01 – «Математика» с дополнительной

специальностью «Информатика»

 

МЕТОДЫ ОПТИМИЗАЦИИ

Научный руководитель: доцент, кандидат технических наук

 

Допущена к защите.

Зав. кафедрой математического анализа _________________________

«___» _______ 2010 г., протокол №__

 

Защищена «____» июня 2010 г.

 

Оценка __________________________

 

СОДЕРЖАНИЕ

	Стр.
Введение………………………………………………………………………	3
Глава I. Задача отыскания экстремума функций многих переменных…............................................................................................	5
§1. Функция многих переменных………………………………………….	5
1.1 Необходимые условия экстремума…………………………….	6
1.2 Необходимые условия второго порядка. Достаточные  условия……………………………………………………………….	8
§2. Относительный экстремум. Метод множителей Лагранжа…………	11
2.1 Метод исключения………………………………………………	11
2.2 Метод множителей Лагранжа………………………………….	12
2.3 Седловая точка функции Лагранжа……………………………..	15
Глава II. Численные методы отыскания безусловного экстремума…….	19
§1. Методы первого порядка (градиентные методы)……………………..	19
1.1 Метод градиентного спуска с постоянным шагом……………	19
1.2 Метод наискорейшего градиентного спуска………………….	25
1.3 Метод покоординатного спуска……………………………….	29
§2. Методы второго порядка………………………………………………	36
2.1 Метод Ньютона………………………………………………….	36
2.2 Метод Ньютона-Рафсона……………………………………….	41
Заключение……………………………………………………………………	46
Литература…………………………………………………………………….	47

Введение

В настоящее время оптимизация находит применение в науке, технике и в любой другой области человеческой деятельности.

Оптимизация- целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.

Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др). Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев - невозможно.

Оптимизация как раздел математики существует достаточно давно. Оптимизация - это выбор, т.е. то, чем постоянно приходится заниматься в повседневной жизни. Термином "оптимизация" в литературе обозначают процесс или последовательность операций, позволяющих получить уточненное решение. Хотя конечной целью оптимизации является отыскание наилучшего или "оптимального" решения, обычно приходится довольствоваться улучшением известных решений, а не доведением их до совершенства. По этому под оптимизацией понимают скорее стремление к совершенству, которое, возможно, и не будет достигнуто.

На первоначальном этапе решения принимались без специального математического анализа, просто на основе опыта и здравого смысла.

Практика порождает все новые и новые задачи оптимизации причем их сложность растет. Требуются новые математические модели и методы, которые учитывают наличие многих критериев, проводят глобальный поиск оптимума. Другими словами, жизнь заставляет развивать математический аппарат оптимизации.

Из всего выше сказанного можно сделать вывод об актуальности темы дипломной работы.

Объект исследования: методы оптимизации как раздел математики.

Предмет исследования: методы оптимизации первого порядка (градиентные методы) и второго порядка: методы Ньютона и Ньютона- Рафсона.

Цель работы: изучить вопросы отыскания экстремума функции нескольких переменных, а также рассмотреть алгоритмы численных методов отыскания безусловного экстремума.

Задачи, решаемые в работе:

1. Изучить теорию нахождения безусловного и условного экстремумов функции нескольких переменных;

2. Рассмотреть задачи минимизации функции нескольких переменных;

3. Изучить численные методы решения задач поиска безусловного минимума функции.

В первой главе сделан анализ теоретического материала, посвященного пониманию природы задач оптимизации — выведены необ­ходимые и достаточные условия, которым должна удовлет­ворять функция в экстремальных точках. Рассмотрен метод множителей Лагранжа.

Во второй главе изложены численные методы отыскания безусловного экстремума, рассмотрены алгоритмы и примеры градиентных методов оптимизации: градиентного спуска с постоянным шагом, наискорейшего градиентного спуска, покоординатного спуска. Также рассмотрены методы второго порядка: метод Ньютона и метод Ньютона-Рафсона.

 

Глава I . ЗАДАЧА ОТЫСКАНИЯ ЭКСТРЕМУМА ФУНКЦИИ

МНОГИХ ПЕРЕМЕННЫХ

Функция многих переменных

Одной из важных задач анализа является задача оты­скания экстремума (наибольшего или наименьшего зна­чения) скалярной функции f (х) n-мерного векторного аргумента х при некоторых ограничениях. Эту задачу мы будем записывать следующим образом:

min f ( x ),                                                  (1)

                                                 (2)

Здесь X — некоторое подмножество n-мерного евклидова пространства Е_п. Будем называть X допустимым множеством задачи (1)—(2), а точки, принадлежащие X, — ее допустимыми точками. Заметим, что задачу мак­симизации функции f (х) тоже можно записать в виде (1)-(2), заменив f (х) на .

В этой главе будут последовательно рассмотрены задача нахождения безусловного экстремума функции нескольких переменных (Х=Е_п) и задача на относительный экстремум, т. е. задача мини­мизации функции нескольких переменных при наличии ограничений типа равенств, когда X - множество решений уравнения

g ( x )=0,

где g ( x ) есть m-мерная вектор-функция, т<п.

Задача (1) - (2) является классической и рассмат­ривается во всех курсах анализа. Теория решения таких задач развивалась еще в трудах Эйлера, Лагранжа, Бернулли, Лейбница. Она не потеряла своего значения и в настоящее время, несмотря на то, что с тех пор раз­работаны более общие методы, включающие классические, как частый случай. Классическая теория содержит зна­чительную часть идей, лежащих в основе современных методов оптимизации.

 

1.1 Необходимое условие экстремума. Рассмотрим задачу безусловной минимизации, будем теперь счи­тать, что f (х) — скалярная функция векторного аргумента размерности п, т. е. X = E_n. Если - точка ее безусловного локального экстремума, в ^j будет достигаться экстре­мум функции

одной переменной x^j , которая получается из функции f ( x ),  если зафиксировать все переменные, кроме x^j , положив х ⁱ = ⁱ для . Для функции же одной переменной

получена теорема 1.

 Теорема 1. Для того чтобы функция f ( x ), опре­деленная на вещественной оси, имела безусловный локаль­ный экстремум в точке , необходимо, чтобы выполнялось условие

.                                        (3)

Проведя это рассуждение для всех j = 1, ..., п, приходим к следующей теореме.

Теорема 2. Для того чтобы в точке  функция f ( x ¹ , ..., х^п) имела безусловный локальный экстремум, необходимо, чтобы все ее частные производные обращались в  в нуль:

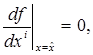 i =1, 2, …n. .                             (4)

Условие стационарности (4) мы будем записывать еще в одной из следующих эквивалентных форм:

grad

где — n-мерный вектор с компонентами , i=l, ..., п, который принято называть градиен­том функции f (х) в точке .

Заметим, что необходимое условие экстремума (4) эквивалентно равенству нулю дифференциала функции f ( x ) в точке :

df ( ) = 0.

В самом деле, если выполнено условие (4), то для любых dx^l , i = l, ..., n, имеем

.

Справедливо и обратное утверждение, так как из послед­него равенства в силу произвольности независимых при­ращений dxⁱ, i = l, ..., n, следует, что все частные производные в точке  равны нулю:

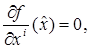 i = l, ..., n.

Условия (4) образуют систему п уравнений для определения п компонент вектора . Эти уравнения могут иметь различную природу и допускать любое количество решений, в частности, не иметь ни одного. Как и выше, точки ,являющиеся решениями системы уравнений (4), будем называть стационарными, а условие (4) - необхо­димым условием экстремума первого порядка.

1.2 Необходимое условие второго порядка. Достаточные условия. После того как решение  системы уравнений (4) будет найдено, необходимо еще определить характер стационарной точки . Для этого нужно исследовать пове­дение функции f ( x ) в окрестности стационарной точки . Снова воспользуемся разложением функции f (х) в ряд Тейлора, предполагая ее дважды непрерывно дифферен­цируемой по всем переменным х¹, ..., х ⁿ . Тогда получим

              (5)

Здесь через  мы обозначили элементы матрицы вто­рых производных функции f ( x ) в стационарной точке , а через 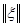 - какую-нибудь норму вектора , например, .Далее матрицу вторых производных мы будем обозначать так:

.                               (6)

Характер стационарной точки  функции f ( x ) связан сознакоопределенностью квадратичной формы

.                             (7)

Напомним, что квадратичная форма называется неотрица­тельно определенной в точке , если

                                  (8)

и положительно определенной, если

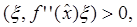                                                        (9)

для любых векторов .

Соответственно, симметричная матрица вторых произ­водных f "(х) называется неотрицательно определенной в точке , если выполнено (8), и положительно опре­деленной, если выполнено (9). Неположительно опреде­ленным и отрицательно определенным квадратичным фор­мам и матрицам соответствуют противоположные знаки в неравенствах (8), (9).

Таким образом, с учетом разложения (5), приходим к следующей формулировке условий второго порядка экстремальности функции f ( x ¹ , ..., х^п).

Теорема 3. Для того чтобы дважды непрерывно дифференцируемая функция п переменных f ( x ) имела в ста­ционарной точке  безусловный локальный минимум (мак­симум), необходимо, чтобы матрица ее вторых производных была неотрицательно (неположительно) определенной, и достаточно, чтобы она была положительно (отрица­тельно) определенной.

Проверка знакоопределенности матриц может быть осу­ществлена, например, с помощью критерия Сильвестра. Согласно этому критерию, необходимым и достаточным условием положительной определенности квадратичной формы (х, Ах), где А = { a_ij } — симметричная 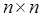 матрица, является выполнение п неравенств:

, , …,

Необходимым и достаточным условием отрицательной опре­деленности квадратичной формы (х, Ах) является выпол­нение цепочки следующих п неравенств:

, , …,

 

Если квадратичная форма не меняет знака, но обра­щается в нуль при ненулевых значениях аргумента, то для определения характера стационарной точки  требу­ется исследование производных более высокого порядка.

Пример. Определить экстремаль­ные значения функции

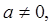
Из необходимых условий (2.1) имеем

Поэтому ,  - стационарная точка. Коэффици­енты квадратичной формы (7), вычисленные в ней, равны

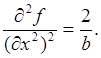
Тогда, согласно теореме 3, имеем следующие случаи:

1) а>0, b >0    - функция f (х) имеет в точке  = {0, 0}^T минимум;

экстремума нет

4) а<0, b<0   - функция f (х) имеет в точке  ={0, 0}^T  максимум. Отметим, что случаи 1) и 4) соответствуют поверхности, являющейся эллиптическим  параболоидом, а случаи 2) и 3) - гиперболическому параболоиду, имеющему стационар­ную точку типа «седло».

Замечание: Здесь и далее {x ¹ , ..., х^п}^T – вектор-столбец.