 |
Главная |
Методы второго порядка
|
из
5.00
|
Метод Ньютона
Процесс отыскания минимума с помощью метода Ньютона оказывается более эффективным (т.е. требует меньшего числа итераций), чем градиентные методы, так как квадратичная функция локально аппроксимирует минимизируемую функцию, чем линейная, лежащая в основе градиентных методов.
Основные недостатки метода Ньютона состоят в том, что он, во-первых, предполагает вычисление вторых производных, что может быть связано с существенными трудностями, и, во-вторых, может расходиться, если целевая функция не является сильно выпуклой и начальное приближение находится достаточно далеко от минимума.
Стратегия поиска
Стратегия метода Ньютона [ Newton I. ] состоит в построении последовательности точек {х k}, k = 0,1,..., таких, что 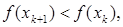 k = 0,1,.... Точки последовательности вычисляются по правилу
k = 0,1,.... Точки последовательности вычисляются по правилу
 (5)
(5)
где х0 задается пользователем; величина шага  определяется для каждого значения k по формуле
определяется для каждого значения k по формуле
 . (6)
. (6)
Выбор  по формуле (6) гарантирует выполнение требования
по формуле (6) гарантирует выполнение требования  при условии, что
при условии, что  . Формула (6) получена из следующих соображений:
. Формула (6) получена из следующих соображений:
1. Функция f (х) аппроксимируется в каждой точке последовательности {х k} квадратичной функцией 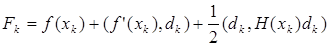 .
.
2. Направление  определяется из необходимого условия экстремума первого порядка:
определяется из необходимого условия экстремума первого порядка:  Таким образом, при выполнении требования
Таким образом, при выполнении требования  последовательность является последовательностью точек минимумов квадратичных функций Fk , k = 0,1,... (рис. 8). Чтобы обеспечить выполнение требования
последовательность является последовательностью точек минимумов квадратичных функций Fk , k = 0,1,... (рис. 8). Чтобы обеспечить выполнение требования 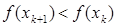 , k = 0,1,..., даже в тех случаях, когда для каких-либо значений матрица Гессе
, k = 0,1,..., даже в тех случаях, когда для каких-либо значений матрица Гессе  не окажется положительно определенной, рекомендуется для соответствующих значений k вычислить точку
не окажется положительно определенной, рекомендуется для соответствующих значений k вычислить точку  по методу градиентного спуска
по методу градиентного спуска  с выбором величины шага
с выбором величины шага  из условия
из условия  .
.

Рис. 8
Построение последовательности {х k} заканчивается в точке х k, для которой  где
где  - заданное малое положительное число, или при
- заданное малое положительное число, или при  (М - предельное число итераций), или при двукратном одновременном выполнении двух неравенств
(М - предельное число итераций), или при двукратном одновременном выполнении двух неравенств  ,
, 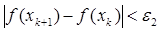 где
где  - малое положительное число. Вопрос о том, может ли точка х k рассматриваться как найденное приближение искомой точки минимума, решается путем проведения дополнительного исследования, которое описано ниже.
- малое положительное число. Вопрос о том, может ли точка х k рассматриваться как найденное приближение искомой точки минимума, решается путем проведения дополнительного исследования, которое описано ниже.
Сходимость
Утверждение. Пусть f ( x ) дважды непрерывно дифференцируемая сильновыпуклая функция с константой l > 0 на Rn и удовлетворяет условию

 ,
,
где L > 0, а начальная точка такова, что 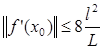 , т.е.
, т.е.
 ,
,
где  .. Тогда последовательность { xk } сходится к точке минимума с квадратичной скоростью
.. Тогда последовательность { xk } сходится к точке минимума с квадратичной скоростью  .
.
Замечание 1. Сходимость метода Ньютона доказана лишь для сильно выпуклых функций и для достаточно хорошего начального приближения, определяемого условием  , практическое использование которого крайне затруднено, так как постоянные l и L , как правило, неизвестны или требуют трудоемкого исследования для их определения. Поэтому при практическом использовании метода Ньютона следует:
, практическое использование которого крайне затруднено, так как постоянные l и L , как правило, неизвестны или требуют трудоемкого исследования для их определения. Поэтому при практическом использовании метода Ньютона следует:
а) анализировать матрицу Н(х k)на выполнение условия Н(х k) < 0  и заменять формулу
и заменять формулу 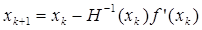 на формулу
на формулу  в случае его невыполнения;
в случае его невыполнения;
б) производить анализ точки х k с целью выяснения, является ли она найденным приближением искомой точки х*.
Замечание 2. При решении задачи поиска безусловного максимума формула (6) не изменяется, так как в этом случае Н(х k ) < 0.
|
из
5.00
|
Обсуждение в статье: Методы второго порядка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

