Метод наискорейшего градиентного спуска

Стратегия поиска

Стратегия решения задачи состоит в построении последовательности точек {х _k}, k = 0,1,..., таких, что  k = 0,1,.... Точки последовательности {х _k} вычисляются по правилу

                      (2)

где точка х₀ задается пользователем; величина шага  определяется для каждого значения k из условия

                     (3)

Решение задачи (3) может осуществляться с использованием необходи­мого условия минимума  с последующей проверкой достаточного условия минимума . Такой путь может быть использован либо при достаточно простой минимизируемой функции , либо при предварительной аппроксимации достаточно сложной функции  полиномом P ( ) (как правило, второй или третьей степени), и тогда условие 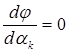 замещается условием 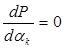, а условие  условием .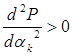

Построение последовательности {х _k}, k = 0,1,..., заканчивается в точке х _k, для которой , где  - заданное число, или, если , М -предельное число итераций, или при двукратном одновременном выполнении неравенств 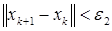, , где  - малое положительное число. Вопрос о том, может ли точка х _k рассматриваться как найденное при­ближение искомой точки локального минимума х_*, решается путем дополни­тельного исследования.

Рис. 4

Геометрическая интерпретация метода для п = 2приведена на рис. 4.

 

Пример 1. 2. Найти локальный минимум функции

.

□ I. Определение точки х _k, в которой выполнен по крайней мере один из критериев окончания расчетов.

1. Зададим х₀, , , 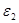М: х₀ = (0,5; 1)^T, = 0,1; 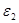= 0,15 ; М = 10. Найдем градиент функции в произвольной точке

2. Положим k = 0.

3⁰. Вычислим 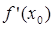: 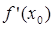= (3;2,5)^Т.

4⁰. Вычислим : = 3,9 > 0,1. Переходим к шагу 5.

5⁰. Проверим условие : k = 0 < 10 = M . Переходим к шагу 6.

6° . Следующая точка находится по формуле

= (0,5; 1)^T - (3; 2,5)^г = (0,5 - 3 ; 1 - 2,5 ).

Подставим полученные выражения 0,5 - 3 , 1 - 2,5  для коор­динат в f ( x ): 

 Найдем минимум функции  по 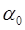 с помощью необходимых условий безусловного экстремума:

.

Отсюда . Так как  = 63,25 > 0, найденное значение шага обеспечивает минимум функции  по .

7⁰. Найдем : х₁ = (0,5; 1)^Т - 0,24(3; 2,5)^Т = (-0,22; 0,4)^Т .

8°. Вычислим  и :

= 0,937 >0,15; 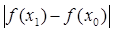= 1,83 > 0,15.

Вывод: полагаем k = 1 и переходим к шагу 3.

3¹. Вычислим 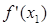: 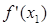= (-0,48; 0,58)^T.

4¹. Вычислим 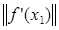= 0,752 > 0,1.

5¹. Проверим условие : k = 1 < 10 = М.

6¹. Определим : = 0,546 (см. п. 6⁰).

7¹. Найдем :

х₂ =(-0,22; 0,4)^T - 0,546 (- 0,48; 0,58)^T = (0,04; 0,08)^T.

8¹. Вычислим  и :

= 0,41 > 0,15; = 0,156 > 0,15.

Полагаем k = 2 и переходим к шагу 3.

3². Вычислим : = (0,24; 0,2)^T.

4². Вычислим : = 0,312 > 0,1.

5². Проверим условие : k = 2 < 10 = M.

6². Определим : =0,24 (см. п. 6⁰).

7². Найдем :

х₃ =(0,04; 0,08)^T - 0,24 (0,24; 0,2)^T = (-0,0176; 0,032)^T.

8² . Вычислим 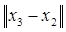 и :

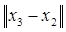= 0,0749 < 0,15; = 0,0116 < 0,15.

Полагаем k =3 и переходим к шагу 3.

3³. Вычислим : = (-0,012; -0,0816)^T.

4³. Вычислим : = 0,082 < 0,1. Расчет окончен. Найдена точка х₃ =(-0,0176; 0,032)^T,  f (х₃) = 0,00127.

II. Анализ точки х₃.

В примере 1.1 (гл.2 §1) было показано, что функция f ( x ) является строго выпуклой и, следовательно, точка х₃  является найденным приближением точки глобаль­ного минимума х_*. ■

Метод покоординатного спуска

Стратегия поиска

Стратегия решения задачи состоит в построении последовательности точек {х _k}, k = 0,1,..., таких, что 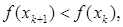 k = 0,1,... . Точки последовательности {х _k}вычисляются по циклам в соответствии с правилом

.                         (4)

где j - номер цикла вычислений; j = 0,1,2,...; k - номер итерации внутри цикла, k = 0,1,...,n -1; е _{k +1} , k = 0,l,..., n- 1 -единичный вектор, (k+1) -я проекция ко­торого равна 1; точка х₀₀ задается пользователем, величина шага 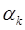 выбирается из условия

 или .

Если выбранное условие при текущем 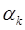 не выполняется, шаг уменьшается вдвое и точка  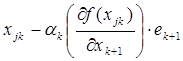вычисляется заново. Легко видеть, что при фиксированном j за одну итерацию с номером k изменяется только одна проекция точки х _jk, имеющая номер k +1, а в течение всего цикла с номером  j , т.е. начиная с k = 0 и кончая k = п -1, изменяются все п проекций точки х _{j 0}. После этого точке х _{j п} присваивается номер х _{j + 0,1}, и она берется за на­чальную точку для вычислений в  j + 1 цикле. Расчет заканчивается в точке х _jk при выполнении по крайней мере одного из трех критериев окончания счета: , или , или двукратного выполнения неравенств , .

Полученные в результате вычислений точки могут быть записаны как эле­менты последовательности {х _l}, где  - порядковый номер точки, т.е.  

Геометрическая интерпретация метода для п = 2 приведена на рис. 5.

Рис. 5

Пример 1.3. Найти локальный минимум функции

.

□ I. Определение точки x_jk, в которой выполнен по крайней мере один из критериев окончания расчетов.

1. Зададим х₀₀, М:  х₀₀ = (0,5; 1)^Т, 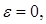; М=10. Найдем градиент функции в произвольной точке

2. Зададим j = 0.

3⁰. Проверим выполнение условия 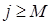:  j = 0<10 = М.

4⁰. Зададим k = 0.

5⁰. Проверим выполнение условия : k = 0<1 = n-1.

6⁰. Вычислим : = (3; 2,5)^T.

7⁰. Проверим условие : = 3,8 > 0,1.

8⁰. Зададим  = 0,5 .

9⁰. Вычислим , где

, .

Отсюда х₀₁ = (-1;1)^T.

10⁰. Проверим условие : = 2-2 = 0. Вы­вод: полагаем  = 0,25 и переходим к шагу 9.

9⁰¹. Вычислим х₀₁ с шагом  = 0,25: х₀₁ = (-0,25; 1)^T.

10⁰¹. Проверим условие :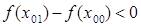

= 0,875 - 2 = -1,125 < 0.

11⁰. Проверим условия , :

= 0,75 > 0,15; = 1,125 > 0,15.

Полагаем k =1 и переходим к шагу 5.

5¹. Проверим условие : k = 1 = n-1.

6¹. Вычислим : = (0; 1,75)^T.

7¹. Проверим условие : = 1,75 > 0,1.

8¹. Зададим =0,5.

9¹. Вычислим , где ;

.

Отсюда х₀₂ = (-0,25; 0,125)^Т .

10¹. Проверим условие :

= 0,109 - 0,875 = - 0,766 < 0.

11¹. Проверим условия , :

= 0,875 > 0,15, = 0,766 > 0,15.

Полагаем k = 2, переходим к шагу 5.

5². Проверим условие : k = 2 > n -1. Зададим j = 1, х₁₀ = х₀₂, пе­реходим к шагу 3.

3¹. Проверим условие 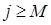: j = 1 < 10 = М.

4¹. Зададим k = 0.

5². Проверим условие : k = 0 <1 = п-1.

6². Вычислим : = = (-0,875; 0,00)^T .

7². Проверим условие 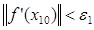: 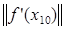= 0,875 > 0,1.

8² . Зададим  = 0,25.

9². Вычислим :  x ₁₁ = (-0,03;0,125)^T

10². Проверим условие :

= 0,01-0,109 = -0,099 < 0.

11². Проверим условия , :

= 0,22 > 0,15, = 0,099 < 0,15.

Полагаем k =1 и переходим к шагу 5.

5³. Проверим условие : k = 1 = n -1.

6³. Вычислим : = (0,005; 0,22)^T .

7³. Проверим условия : = 0,22 > 0,1.

8³. Зададим 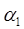 =0,25.

9³. Вычислим : x ₁₂ =(-0,03; 0,07)^T.

10³. Проверим условие :

= 0,0046 -0,01 = -0,0054 < 0.

11³. Проверим условия , :

= 0,055 < 0,15, 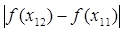= 0,0054 < 0,15.

Зададим k = 2 и переходим к шагу 5.

5⁴. Проверим условие : k = 2 > п-1.

Полагаем j = 2, х₂₀ = х₁₂ и переходим к шагу 3.

3² . Проверим условие 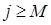: j = 2 < 10 = М.

4². Зададим k =0.

5⁴. Проверим условие : k = 0 <1 = n -1.

6⁴. Вычислим : = = (-0,05; 0,11)^T.

7⁴. Проверим условие 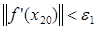: = 0,12 > 0,1.

8⁴ . Зададим = 0,25.

9⁴. Вычислим : х₂₁ = (- 0,02; 0,07)^Т.

10⁴. Проверим условие : 0,0043-0,046 = -0,0003 < 0, пе­рейдем к шагу 11.

11⁴. Проверим условия , :

= 0,01 < 0,15 , = 0,0003 < 0,15.

Условия ,  выполнены в двух последовательных циклах с номерами j = 2 и j -1 = 1. Расчет окончен, найдена точка х₂₁ = (- 0,02; 0,07)^Т; f (х₂₁) = 0,0043 .

На рис. 6 полученные точки соединены пунктирной линией.

В методе покоординатного спуска мы спускаемся по ломаной, состоящей из отрезков прямых, параллельных координатным осям.

Рис. 6

II. Анализ точки х₂₁.

В примере 1.1 (гл.2 §1) было показано, что функция f (х) строго выпукла, имеет единственный минимум и, следовательно, точка х₂₁ = = (-0,02; 0,07)^Т является найденным приближением точки глобального минимума. ■

Во всех рас­смотренных выше градиентных методах последовательность точек { x_k } сходится к стационарной точке функции f ( x ) при достаточно общих предложениях относительно свойств этой функции. В частности, справедлива теорема:

Теорема. Если функция f ( x ) ограничена снизу, ее градиент удовлетворяет условию Липшица ( ) и выбор значения  производится одним из описанных выше спосо­бов, то, какова бы ни была начальная точка х₀:

 при .

При практической реализации схемы

      k =1, 2, … n .

итерации прекращаются, если для всех i, i = 1, 2, ..., n, выпол­нены условия типа

,

где  - некоторое заданное число, характеризующее точ­ность нахождения минимума.

В условиях теоремы градиентный метод обеспечи­вает сходимость по функции либо к точной нижней грани 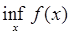 (если функция f (х) не имеет минимума; рис. 7), либо к значению функции в некоторой стационарной точке, являющейся пределом последовательности {х_к}. Нетрудно придумать примеры, когда в этой точке реализуется седло, а не минимум. На практике ме­тоды градиентного спуска уверенно обходят седловые точки и находят минимумы целевой функции (в общем случае — локальные).

Рис. 7