 |
Главная |
Численные методы решения обыкновенных дифференциальных уравнений
|
из
5.00
|
Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функции y=y (x). Их можно записать в виде
 , где х - независимая переменная.
, где х - независимая переменная.
Наивысший порядок n входящей в уравнение  производной называется порядком дифференциального уравнения.
производной называется порядком дифференциального уравнения.
Методы решения обыкновенных дифференциальных уравнений можно разбить на следующие группы: графические, аналитические, приближенные и численные.
Графические методы используют геометрические построения.
Аналитические методы встречаются в курсе дифференциальных уравнений. Для уравнений первого порядка (с разделяющимися переменными, однородных, линейных и др.), а также для некоторых типов уравнений высших порядков (например, линейных с постоянными коэффициентами) удается получить решения в виде формул путем аналитических преобразований.
Приближенные методы используют различные упрощения самих уравнений путем обоснованного отбрасывания некоторых содержащихся в них членов, а также специальным выбором классов искомых функций.
Численные методы решения дифференциальных уравнений в настоящее время являются основным инструментом при исследовании научно-технических задач, описываемых дифференциальными уравнениями. При этом необходимо подчеркнуть, что данные методы особенно эффективны в сочетании с использованием современных компьютеров.
Метод Эйлера
Простейшим численным методом решения задачи Коши для ОДУ является метод Эйлера. Рассмотрим уравнение  в окрестностях узлов
в окрестностях узлов  (i=1,2,3,…) и заменим в левой части производную
(i=1,2,3,…) и заменим в левой части производную  правой разностью. При этом значения функции
правой разностью. При этом значения функции  узлах
узлах  заменим значениями сеточной функции
заменим значениями сеточной функции  :
:

Полученная аппроксимация ДУ имеет первый порядок, поскольку при замене  на
на  допускается погрешность
допускается погрешность 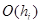 .
.
Будем считать для простоты узлы равноотстоящими, т.е.  Тогда из равенства
Тогда из равенства  получаем
получаем

Заметим, что из уравнения  следует
следует
 .
.
Поэтому  представляет собой приближенное нахождение значение функции
представляет собой приближенное нахождение значение функции  в точке
в точке  при помощи разложения в ряд Тейлора с отбрасыванием членов второго и более высоких порядков. Другими словами, приращение функции полагается равным её дифференциалу.
при помощи разложения в ряд Тейлора с отбрасыванием членов второго и более высоких порядков. Другими словами, приращение функции полагается равным её дифференциалу.
Полагая i=0, с помощью соотношения 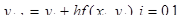 находим з значение сеточной функции
находим з значение сеточной функции  при
при  :
:
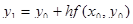 .
.
Требуемое здесь значение  задано начальным условием
задано начальным условием  , т.е.
, т.е.
 .
.
Аналогично могут быть найдены значения сеточной функции в других узлах:

Построенный алгоритм называется методом Эйлера

Рисунок - 19 Метод Эйлера
Геометрическая интерпретация метода Эйлера дана на рисунке. Изображены первые два шага, т.е. проиллюстрировано вычисление сеточной функции в точках  . Интегральные кривые 0,1,2 описывают точные решения уравнения
. Интегральные кривые 0,1,2 описывают точные решения уравнения  . При этом кривая 0 соответствует точному решению задачи Коши, так как она проходит через начальную точку А (x0,y0). Точки B,C получены в результате численного решения задачи Коши методом Эйлера. Их отклонения от кривой 0 характеризуют погрешность метода. При выполнении каждого шага мы фактически попадаем на другую интегральную кривую. Отрезок АВ - отрезок касательной к кривой 0 в точке А, ее наклон характеризуется значением производной
. При этом кривая 0 соответствует точному решению задачи Коши, так как она проходит через начальную точку А (x0,y0). Точки B,C получены в результате численного решения задачи Коши методом Эйлера. Их отклонения от кривой 0 характеризуют погрешность метода. При выполнении каждого шага мы фактически попадаем на другую интегральную кривую. Отрезок АВ - отрезок касательной к кривой 0 в точке А, ее наклон характеризуется значением производной  . Погрешность появляется потому, что приращение значения функции при переходе от х0 к х1 заменяется приращением ординаты касательной к кривой 0 в точке А. Касательная ВС уже проводится к другой интегральной кривой 1. таким образом, погрешность метода Эйлера приводит к тому, что на каждом шаге приближенное решение переходит на другую интегральную кривую.
. Погрешность появляется потому, что приращение значения функции при переходе от х0 к х1 заменяется приращением ординаты касательной к кривой 0 в точке А. Касательная ВС уже проводится к другой интегральной кривой 1. таким образом, погрешность метода Эйлера приводит к тому, что на каждом шаге приближенное решение переходит на другую интегральную кривую.
|
из
5.00
|
Обсуждение в статье: Численные методы решения обыкновенных дифференциальных уравнений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

