 |
Главная |
Построение модели прогнозирования финансовой устойчивости торгового предприятия «Дулгис»
|
из
5.00
|
Необходимым условием осуществления последовательных расчетных операций при построении модели прогнозирования финансовой устойчивости предприятия, влияния на нее подсистем нормативно-правового обеспечения и исследования привлекательности товаров и услуг является предварительное определение наличия или отсутствия тренда в динамическом ряду параметров, характеризующих фактический объем товарооборота в каждом из обозначенных периодов в «Дулгис».
Наличие или отсутствие тренда основано на использовании метода средних уровней. Для этого динамический ряд разбивается на две равные по числу членов части. Динамический ряд показателей, характеризующих фактическое значение товарооборота в торговом предприятии «Дулгис».представлен в табл. 3.2.1.
Таблица 3.2.1
Товарооборот ООО «ЛаДива» по кварталам за 2007 – 2009гг.
| Год | Товарооборот тыс. руб. |
| I кв. 2007 г. | 5260 |
| II кв. 2007 г. | 5327 |
| III кв. 2007 г. | 5378 |
| IV кв. 2007 г. | 5467 |
| Итого: 21432 | |
| I кв. 2008 г. | 5549 |
| II кв. 2008 г. | 5624 |
| III кв. 2008 г. | 5704 |
| IV кв. 2008 г. | 5755 |
| Итого:22635 | |
| I кв. 2009 г. | 5824 |
| II кв. 2009 г. | 5889 |
| III кв. 2009 г. | 5959 |
| IV кв. 2009 г. | 6033 |
| Итого: 23705 | |
Для выбора вида зависимости между состоянием нормативно-правового обеспечения и подсистемы исследования привлекательности товаров и услуг и фактическим объемом товарооборота торгового предприятия «Дулгис».рекомендуется использовать метод характеристик приростов исследуемого показателя. Этот метод предполагает расчет абсолютных приростов данного показателя.
Для построения экономико-математической модели, необходимо определиться с динамическим рядом. В качестве динамического ряда будут выступать значения товарооборота торгового предприятия «Дулгис» за 2007-2009 гг. разделенные на 12 кварталов. При выявлении тренда воспользуемся методом усреднения по левой и правой половинам. Применяя этот метод, динамический ряд разбивается на две части и находится среднее значение для каждой половины. Динамический ряд представлен в табл. 3.2.2.
Таблица 3.2.2
Разбитие динамического ряда по показателям товарооборота торгового предприятия «Дулгис» за 2007-2009 гг.
| Период | Розничный товарооборот, тыс. руб. | Ряд |
| 1 | 5260 | 1 |
| 2 | 5327 | |
| 3 | 5378 | |
| 4 | 5467 | |
| 5 | 5549 | |
| 6 | 5624 | |
| 7 | 5704 | 2 |
| 8 | 5755 | |
| 9 | 5824 | |
| 10 | 5889 | |
| 11 | 5959 | |
| 12 | 6033 |
Разбиваем данные приведенные в таблице на два ряда по шесть значений. Первый ряд включает значения товарооборота за четыре квартала 2007 года и первых два квартала 2008 года. Ко второму ряду отнесены значения товарооборота а за последние два квартала 2008 года и четыре квартала 2009 года. Данное разделение необходимо, что бы определить коэффициент Фишера и коэффициент Стьюдента, которые в свою очередь позволят определить характер (вид) зависимости между показателями модели. Для расчета данных показателей необходимо знать средние значения товарооборота каждого ряда.


Для выявления тренда необходимо, чтобы соблюдалось условие, при котором расчетное значение критерия Фишера должно быть меньше табличного значения (с учетом доли ошибки в 5%). Расчет коэффициента Фмшера представлен в табл. 3.2.3
Таблица 3.2.3
Расчет коэффициента Фишера
| Коэффициент | Формула | Значение расчетное | Значение табличное |
Коэф. Фишера, 
|  , где , где
 и и

|



|

|
Расчетное значение критерия Фишера = 1,23, табличное значение критерия Фишера = 5,05 (при k1, k2 = 5). При нахождении тренда в динамическом ряду соблюдается условие критерия Фишера. Расчетное значение коэффициента Фишера меньше табличного значения, с долей ошибки в 5%.
Рассчитаем значение критерия Стьюдента. Нахождение данного показателя основывается на средних значениях валового дохода и дисперсии по каждой части динамического ряда. При этом учитывают число степеней свободы k1, k2 = 5. Расчет коэффициента Стьюдента представлен в табл. 3.2.3
Таблица 3.2.3
Расчет коэффициента Стьюдента
| Коэффициент | Формула | Значение расчетное | Значение табличное |
Коэф. Стьюдента

|  ,где ,где
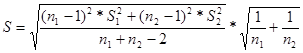
|


|

|
Расчетное значение коэффициента Стьюдента равно 2,24, табличное значение данного коэффициента равно 2,23. Полученное нами расчетное значение больше табличного. Что является необходимым условием при выявлении тренда. Расчетное значение коэффициента Стьюдента больше табличного (  >
>  ).
).
Соблюдение двух этих условий необходимо для выявления тренда в динамическом ряду показателя товарооборота торгового предприятия «Дулгис». Выявление тренда в динамическом ряду позволяет построить уравнение вида 3.1.1 Данное уравнение позволит осуществить процесс прогнозирования товарооборота торгового предприятия «Дулгис»
На значения валового дохода влияют различные факторы. Установление влияния значения валового дохода и факторами влияющих на него необходимо для дальнейшего построения прогнозируемой модели. Выделяют зависимость линейную и нелинейную, которая выражается с помощью функций. Для определения вида зависимости необходимо рассмотреть изменения значений тренда торгового предприятия «Дулгис». Данные об изменении товарооборота торгового предприятия «Дулгис» приведены в табл. 3.2.4
Таблица 3.2.4.
Изменения товарооборота торгового предприятия «Дулгис»
| Квартал | Значение товарооборота, тыс. руб. | Изменение, тыс. руб. |
| 1-й квартал 2007 | 5260 | - |
| 2-й квартал 2007 | 5327 | +67 |
| 3-й квартал 2007 | 5378 | +51 |
| 4-й квартал 2007 | 5467 | +89 |
| 1-й квартал 2008 | 5549 | +82 |
| 2-й квартал 2008 | 5624 | +75 |
| 3-й квартал 2008 | 5704 | +80 |
| 4-й квартал 2008 | 5755 | +51 |
| 1-й квартал 2009 | 5824 | +69 |
| 2-й квартал 2009 | 5889 | +65 |
| 3-й квартал 2009 | 5959 | +70 |
| 4-й квартал 2009 | 6033 | +71 |
Рассматривая значения можно отметить, что рассматриваемые значения товарооборота торгового предприятия «Дулгис» незначительно отличаются между собой отметить, и находятся линейной зависимости, по отношению к фактору времени. Поэтому графическое изображение данной зависимости будет выгладить в виде прямой линии.
В аналитической главе были выявлены наименее развитые подсистемы прогнозирования финансовой устойчивости торгового предприятия «Дулгис», такие как подсистема обеспечения процедуры товародвижения и подсистема анализа товародвижения.
При построении модели прогнозирования необходимо определить количественные значения подсистемы обеспечения процедуры и анализа товародвижения. Для их определения необходимо рассчитать интегральный коэффициент.
 (3.2.1)
(3.2.1)
где К1, К2, К3, К4, К5, К6 - коэффициенты подсистем.
Для расчета интегрального коэффициента необходимо первоначально рассчитать коэффициенты каждой подсистемы в отдельности. После расчета данных коэффициентов будет проведен расчет интегральных.
Расчет коэффициентов подсистемы обеспечения процедуры прогнозирования финансовой устойчивости будет произведен с помощью формул представленных в табл. 3.2.5.
Таблица 3.2.5
Оценка состояния промышленной подсистемы обеспечения процедуры прогнозирования финансовой устойчивости торгового предприятия «Дулгис»
| Коэффициент | Расчетная формула |
| 1. объем, ассортимент, структура, качество продукции | К1= количество наименований товаров с сертификатами качества/общее число наименований товара |
| 2. себестоимость, обеспеченность основными и оборотными средствами и уровень их использования | К2= уровень использования основных и оборотных средств в оценке по 5-балльной шкале/5 |
| 3. экология производства | К3=количество наименований товаров с сертификатами экологичности /общее количество наименований товаров |
| 4. наличие и степень инфраструктуры | К4= оценка инфраструктуры по 5-балльной шкале/5 |
Используя приведенные в табл.3.2.5 формулы необходимо рассчитать значения каждого коэффициента и значение интегрального показателя за исследуемый период.
Данные для расчета коэффициентов представлены в Приложении 1. Расчетные данные приведены в табл. 3.2.6
Таблица 3.2.6
Расчетные значения коэффициентов промышленной подсистемы обеспечение процедуры прогнозирования финансовой устойчивости торгового предприятия «Дулгис»
| Коэф-фициент | Период (квартал) | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1. К1 | 0,66 | 0,67 | 0,67 | 0,69 | 0,69 | 0,69 | 0,69 | 0,70 | 0,71 | 0,71 | 0,71 | 0,71 |
| 2. К2 | 0,8 | 0,8 | 0,6 | 0,8 | 0,6 | 0,8 | 0,8 | 0,6 | 0,8 | 0,8 | 0,6 | 0,8 |
| 3. К3 | 0,66 | 0,67 | 0,67 | 0,69 | 0,69 | 0,69 | 0,69 | 0,70 | 0,71 | 0,71 | 0,74 | 0,74 |
| 4. К4 | 0,8 | 0,8 | 0,8 | 0,8 | 0,8 | 0,6 | 0,6 | 0,6 | 0,8 | 0,6 | 0,8 | 0,8 |
| Кинт | 0,808 | 0,812 | 0,816 | 0,820 | 0,782 | 0,782 | 0,782 | 0,749 | 0,828 | 0,788 | 0,795 | 0,834 |
Полученные расчетные значения интегрального коэффициента за 12 кварталов позволят в дальнейшем рассчитать уравнение регрессии.
Формулы для расчета коэффициентов управленческой подсистемы произведены табл. 3.2.7.
Таблица 3.2.7
Оценка состояния управленческой подсистемы прогнозирования финансовой устойчивости торгового предприятия «Дулгис»
| Коэффициент | Расчетная формула |
| 1. оптимизация состава работников предприятий по количеству | К1= общее количество работников /норма работников на товарооборот |
| 2. оптимизация состава работников предприятий по профессионализму; | К2=количество работников, имеющих профильное образование/общее количество работников |
| 3. эффективное использование труда работников | К3=выработка на 1 работающего/норма выработки на 1 работающего |
Используя приведенные в табл.3.2.7 формулы необходимо рассчитать значения каждого коэффициента и значение интегрального показателя за исследуемый период. Данные для расчета коэффициентов представлены в Приложении 2. Расчетные данные приведены в табл. 3.2.8
Таблица 3.2.8
Расчетные значения коэффициентов управленческой подсистемы прогнозирования финансовой устойчивости торгового предприятия «Дулгис»
| Коэф-фициент | Период (квартал) | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 К1 | 0,92 | 0,92 | 0,92 | 0,92 | 0,92 | 0,88 | 0,88 | 0,88 | 0,85 | 0,85 | 0,85 | 0,85 |
| 2. К2 | 0,60 | 0,60 | 0,60 | 0,60 | 0,62 | 0,62 | 0,62 | 0,62 | 0,59 | 0,59 | 0,59 | 0,59 |
| 3. К3 | 0,76 | 0,76 | 0,76 | 0,76 | 0,73 | 0,73 | 0,73 | 0,73 | 0,72 | 0,72 | 0,72 | 0,72 |
| Кинт | 0,865 | 0,865 | 0,865 | 0,865 | 0,864 | 0,864 | 0,864 | 0,864 | 0,844 | 0,844 | 0,844 | 0,844 |
Определив значения факторов подсистемы обеспечения процедуры, учитывая вид зависимости увеличения товарооборота торгового предприятия «Дулгис», возможно, построить модель разработки прогноза увеличения товарооборота торгового предприятия «Дулгис» с помощью уравнения регрессии.
Уравнение регрессии имеет следующий вид:
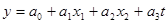 (3.2.2)
(3.2.2)
где  - интегральный коэффициент подсистемы обеспечения процедуры товародвижения ООО «ВеЛОН»;
- интегральный коэффициент подсистемы обеспечения процедуры товародвижения ООО «ВеЛОН»;
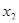 - интегральный коэффициент подсистемы анализа товародвижения ООО «ВеЛОН»;
- интегральный коэффициент подсистемы анализа товародвижения ООО «ВеЛОН»;
 - период времени, для которого разрабатывается прогноз;
- период времени, для которого разрабатывается прогноз;
 ,
,  ,
,  ,
,  - параметры уравнения.
- параметры уравнения.
Прежде чем построить уравнение необходимо оценить ее параметры. Для оценки параметров используем метод наименьших квадратов. При использовании этого метода сумма квадратов значений  ,
, 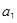 ,
,  ,
,  будет минимальной, с учетом фактических значений
будет минимальной, с учетом фактических значений  от расчетных
от расчетных  . После составляется система уравнений для оценки имеющихся параметров.
. После составляется система уравнений для оценки имеющихся параметров.
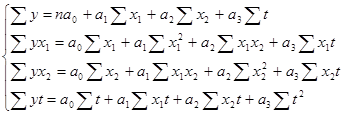
В данную систему уравнений необходимо подставить имеющиеся расчетные значения, которые позволят составить систему уравнений с неизвестными значениями параметров  ,
,  ,
,  ,
,  .
.
Расчетные значения, необходимые для составления данной системы уравнений приведены в Приложении 3. Система уравнений:

Решив данную систему, найдем значения параметров  ,
,  ,
,  ,
, 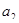 . Получаем:
. Получаем:
 =-1438,07
=-1438,07
 =-1719,55
=-1719,55
 =7028,11
=7028,11
 =302,53
=302,53
Подставим полученые значения парамеитров в исходное уравнение 3.2.2. Тогда уравнение для постранения модели оценки вляиния подсистемы обеспечения процедуры товародвижения и подсистемы анализа товародвижения на пргнозную величину валового дохода будет иметь вид:

После того как построили уравнение, необходимо провести оценку ошибок. Средняя относительная ошибка не должна превышать 5%. Оценка достоверности результатов модели прогнозирования вляиния управленческой подсистемы и производственной подсистемы на прогнозную величину товарооборота торгового предприятия «Дулгис», представлена в табл. 3.2.9. Для расчета неоходимы будут дополнительные значения, расчет которых приведен в Приложении 4.
Таблица 3.2.9
Оценка достоверности результатов модели прогнозирования финансовой устойчивости «Дулгис»
| Ошибка | Формула для расчета | Расчет |
| 1. Стандартная ошибка | 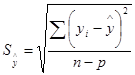 ,
где р – параметр и равен 2, n=12 ,
где р – параметр и равен 2, n=12
|

|
| 2. Среднее линейное отклонение | 
| 
|
| 3. Средняя относительная ошибка | 
| 
|
| 4. Случайная ошибка | 

| 

|
| 5. Фактическое значение критерия Стьюдента | 

| 



|
Расчетное значение средней относительной ошибки составляет 0,004%, данное значение меньше 5%, что позволяет провести оценку значимости параметров модели и построить доверительную зону для нашего уравнения. Расчетное значение стандартной ошибки равно 12,53 тыс. руб., данное значение говорит о том, что отклонение по валовому доходу составляет 12,53 тыс. руб. Оценив значимость параметров уравнения величины, сравниваются с их стандартной ошибкой.
Проводим проверку нулевых гипотез. Для этого необходимо сравнить табличное значение коэффициента Стьюдента и фактическое значение. Табличное значение коэффициента Стьюдента равно 2,23 , при α = 0,05 и к=10. Полученные значения 


 больше табличного значения, поэтому нулевая гипотеза отвергается, следовательно, параметры регрессии существуют.
больше табличного значения, поэтому нулевая гипотеза отвергается, следовательно, параметры регрессии существуют.
|
из
5.00
|
Обсуждение в статье: Построение модели прогнозирования финансовой устойчивости торгового предприятия «Дулгис» |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

