Методика использования визуальных моделей при обучении решению задач на движение

Рассматриваемый способ визуализации представляет собой построение графической модели в координатной плоскости. В координатной плоскости по оси абсцисс откладывается время, по оси ординат соответствующий путь, так как рассматриваются задачи на равномерное прямолинейное движение, то графиками движения объектов, указанных в задачах, будут прямые.

Задачи на равномерное прямолинейное движение можно разделить в зависимости от их графической модели на два типа: те, графические модели которых, непосредственно выражают зависимость между данными и искомыми, и те, чьи модели указывают на упомянутую зависимость, помогают проследить логику построения математической модели.

Задачи первого типа в своей графической модели содержат зависимости между данными и искомым в виде геометрических связей (подобия и равенства треугольников), которые выражают данную зависимость, благодаря чему (из одних лишь геометрических соображений) можно перейти к математической модели задачи.

Из любой графической модели, благодаря только геометрическим соображениям, можно перейти к математической модели, но это не всегда целесообразно. Осуществить указанный переход можно потому, что условия задач и их графические модели изоморфны, но иногда рассуждения с помощью геометрических образов – это не более чем переход от одной терминологии к другой. Такой переход не всегда целесообразен, так как не всегда приводит к элементарной геометрической задаче, поэтому данные задачи выделяются в отдельный тип.

Первый тип задач является эстетически более привлекательным, так как в способе решения есть элемент неожиданности: из геометрических соображений мы получаем решение задачи на движение. Причем такой способ никак не просматривается из условия самой задачи, что и является фактором неожиданности [21]. Такие рассуждения повышают интерес учеников к математике, так как раскрывают связи между различными ее областями. Кроме того, решение, полученное данным способом, будет более лаконичным, простым и наглядным. То есть для решения мы используем более короткий путь, сохраняя при этом строгость рассуждений; все это и делает решения задач данного типа эстетически более привлекательными.

Выше было сказано, что условия задач и их графические модели изоморфны. Поясним, в чем состоит данный изоморфизм. Во-первых, всякое равномерное прямолинейное движение можно описать с помощью линейной функции, и всякая линейная функция может трактоваться как график равномерного прямолинейного движения. Во-вторых, любой объект, указанный в задаче, имеет свой геометрический образ в графической модели: время –­ отрезок на оси абсцисс, расстояние –­ отрезок на оси ординат, моменты встречи ­– точки пересечения графиков, скорость ­– угол наклона графика. Таким образом, всякое изменение условий влечет за собой изменение графической модели и наоборот.

Для того, что бы данный способ визуализации соответствовал формуле наглядности, данной Болтянским (наглядность = изоморфизм + простота), недостает только простоты графической модели. Простота в данном случае понимается как оперирование понятными образами, как осознание указанного изоморфизма. Все это достигается с помощью решения поставленных задач с использованием определенной методики.

Подготовительная работа при обучении моделированию текстовых задач на движение заключается в формировании умений переводить условие задачи на язык графиков и умений «читать» графики.

Мы работаем в системе координат «время-путь». Первой структурной единицей в системе умений и понятий, необходимой для овладения этим методом, является понятие линейной функции и умение интерпретировать ее как зависимость пути от времени равномерно и прямолинейно движущегося объекта. То есть ученик должен уметь выбрать точку отсчета и положительное направление осей координат, понимать, как отражается скорость на поведении графика.

Таким образом, пропевтическая работа, целью которой является диагностирование и устранение (если имеются) пробелов, а так же актуализация знаний с акцентом на данную интерпретацию, может быть организована с помощью задач. Основным требованием в такой задаче является построение по данным условиям графика, и обратная задача – интерпретировать данный график. При этом существенную роль играет варьирование условий в одной и той же задаче, так как это позволяет осознать влияние их в отдельности, помогает проследить динамику изменения поведения графика [4, 15].

Приведем пример такой работы.

Велосипедист выехал из пункта А и через 7 часов прибыл в пункт В, который находится на расстоянии 70 км от пункта А. Изобразите в координатной системе «время-путь» график движения велосипедиста.

В задаче с данным условием целесообразно выбрать пункт А так, чтобы он совпадал с началом координат. Далее нужно варьировать условия, изменяя скорость, время движения, направление движения, точку отсчета пути, точку отсчета времени.

Велосипедист выехал из пункта А и через 7 часов прибыл в пункт В. Изобразите в координатной системе «время-путь» график движения велосипедиста, если известно, что он двигался со скоростью 10 км в час.

При таких условиях график останется тот же самый, здесь нужно акцентировать внимание учеников на то, что график всегда выражает три параметра: расстояние, время, скорость.

Велосипедист выехал из пункта А и через 7 часов прибыл в пункт В, который находится на расстоянии 70 км от пункта А. Второй велосипедист выехал на час позже, и двигался с той же скоростью. Изобразите в координатной системе «время-путь» графики движения велосипедистов.

В этой задаче график движения второго велосипедиста сдвигается параллельным переносом на единицу вниз. Аналогично нужно варьировать начало отсчета пути, пути и времени одновременно. Такое изменение формирует представления о местоположении точки отсчета, которое необходимо для умения моделировать данным способом задачи более сложного содержания.

Велосипедист выехал из пункта А и через 7 часов прибыл в пункт В, который находится на расстоянии 70 км от пункта А. Второй велосипедист выехал на час позже, и прибыл в пункт В одновременно с первым. Изобразите в координатной системе «время-путь» графики движения велосипедистов.

В данной задаче варьируется скорость второго велосипедиста. При изменениях такого рода формируется понимание зависимости угла наклона графика от скорости.

Велосипедист выехал из пункта А и через 7 часов прибыл в пункт В, который находится на расстоянии 70 км от пункта А. Второй велосипедист выехал из пункта В одновременно с первым, и прибыл в А когда первый прибыл в В. Изобразите в координатной системе «время-путь» графики движения велосипедистов.

При данных условиях формируется умение выбирать положительное направление движения. Здесь же можно поставить вопрос о времени или месте встречи велосипедистов, что даст первоначальные представления о сути метода. В данной задаче возможны еще случаи варьирования условий, но вышеуказанные составляют основу, так как остальные из них являются комбинацией первоначальных.

Итак, основополагающими являются умения выбирать точку отсчета по пути и по времени, положительное направление движения, понятие о зависимости угла наклона графика от скорости движения объекта. Достижение всего вышеуказанного происходит в процессе решения задач, подобных приведенным.

Этап обучения графическому моделированию задач на движение во многом опирается на умения, сформированные на предыдущем этапе. Но в данной части есть свои, специфические для данного этапа, особенности. Они заключаются в том, что условия, формулируемые в задаче, не позволяют однозначно построить график отдельного движущегося объекта, так как в них не задаются все те параметры, которые позволяли бы это сделать. Тем не менее, модель должна отображать существенные стороны задачи. Например, условия задачи не позволяют однозначно построить графики двух движущихся объектов, но из них ясно, что если один движется быстрее другого, то и угол наклона у него должен быть больше. Кроме того, на данном этапе нужно сформировать умение рационально строить модели. Этого можно добиться, давая при удобном случае рекомендации по построению модели. К таким рекомендациям можно отнести следующие [3]:

· если в задаче несколько объектов движутся на встречу одному, то удобнее в начало координат поместить эти несколько объектов;

· если в задаче движение начинается в какое-то определенное время суток, которое не влияет существенно на саму задачу, то при построении модели лучше полагать, что движение началось в момент времени;

· если в задаче есть динамика движения (то есть движение объектов относительно друг друга меняется), то удобнее те изменения, которые затрагивают меньшее количество графиков (например, если человека обгоняет рейсовый автобус через временной интервал, то для изображения момента встречи с идущим в другую сторону автобусом рациональнее развернуть график пешехода, чем совокупность прямых, изображающих движение рейсового автобуса).

Аккуратность чертежа хотя сама собой разумеется, но следует сделать акцент на то, что модель которая наиболее точно воспроизводит пропорции, указанные в задаче, может оказать существенную помощь в поиске решения задачи, тем более если эта задача первого типа.

Таким образом, модель становится схематичной, но, несмотря на это должна отражать существенные стороны задачи, так как это необходимое (а во многом и достаточное) условие успешности решения задачи [23].

В связи с этим необходимо обучать моделированию в данных условиях, что подразумевает под собой поэтапное движение от схематичного моделирования условий с двумя движущимися объектами к моделированию сложных условий с тремя и более движущимися объектами (например, периодическое движение рейсового автобуса). Необходимо также умение «читать» модели, то есть понимать, какой объект движется быстрее, какой раньше прибыл, где или когда они встретились. Значит, ученики должны выполнить работу по составлению моделей, по интерпретации моделей, по исправлению сознательно допущенных в ней ошибок, по составлению задач по данной модели.

Приведем примеры заданий, которые можно использовать на данном этапе.

Из пунктов А и В одновременно навстречу друг другу вышли два пешехода. После встречи первый находился в пути 16 минут, а второй 25 минут. Составьте модель данной задачи.

Данная задача не позволяет однозначно строить графики движения пешеходов, но подразумевает, что первый двигался быстрее, это должно быть отражено в модели. Для более хорошего освоения и закрепления можно дать еще 1-2 такие задачи.

Далее моделируемые ситуации должны усложняться, в условие должны входить 3 или более объектов, вместе с этим, как следствие возрастает количество числовых данных о вообще объем задачи, следовательно, усиливается роль анализа, умения выделить главные существенные стороны задачи.

Пешеход и велосипедист одновременно из одной точки направились навстречу всаднику. В момент, когда велосипедист встретил всадника, пешеход отставал от них на 3 км. В момент, когда пешеход встретил всадника, велосипедист обогнал пешехода на 6 км. Составьте модель данной задачи.

В этой задаче нужно выбрать положительное направление. Конечно, рациональнее выбор, при котором в положительном направлении движутся пешеход и велосипедист, но нужно показать оба случая для формирования умения рационально строить модель и понимания разновариантности. Кроме того, здесь уже три движущихся объекта, и подразумевается, но явно не сказано, что велосипедист движется быстрее пешехода.

Наращивая уровень сложности нужно дать задание подобного рода.

Идущего по дороге с постоянной скоростью человека рейсовый автобус обгоняет через каждые 7 минут, а через каждые 5 минут проходит встречный автобус. Составьте модель данной задачи.

Далее идут задачи, в которых по данной модели требуется определить числовые, или сравнительные характеристики движущегося объекта. Например, по данному рисунку определить какой объект двигался быстрее, где место встречи по отношению к началу и концу пути?

И, наконец, задания на составление задачи по модели.

Следующий этап предполагает непосредственное применение графических моделей для решения данного класса задач. В начале естественнее будет рассмотреть задачи первого типа, совместно провести анализ задачи, опираясь на графическую модель, перейти к математической модели.

Если мы рассматриваем задачи первого типа, то существенной чертой данного этапа является абстрагирование от функциональной части модели, и рассмотрение ее с позиций геометрии. То есть ученик должен уметь видеть геометрические отношения в данной модели, а так же уметь интерпретировать эти отношения в терминах данной задачи. Провести анализ задачи в данном случае означает выделить геометрический образ неизвестного, и идти от него к данным, устанавливая геометрические связи. Как правило, неизвестным бывает длина отрезка, в результате анализа задачи она выражается через данные, тем самым мы переходим к математической модели данной задачи. Строить графические модели, выделять геометрические образы неизвестных ученики умеют с предыдущих двух этапов, на этом этапе им нужно научиться проводить анализ задачи, используя графическую модель, что достигается путем выполнения упражнений. Приведем пример анализа подобной задачи и методической работы с ней.

Задача 6.Из пунктов А и В одновременно навстречу друг другу вышли два пешехода. После встречи первый находился в пути 16 минут, а второй 25 минут. Сколько времени каждый из них находился в пути?

Ученики владеют методами построения модели. Пусть модель построена (рис. 6), перейдем к ее анализу. Введем предварительно обозначения всех точек пересечения прямых, а через точку С проведем перпендикуляр МК к оси абсцисс. В задаче требуется найти время нахождения в пути обоих пешеходов, время движения каждого после встречи известно, следовательно, неиз вестным является время движения до момента встречи. Геометрическим образом неизвестного будет отрезок ВК. Заметим, что величину x мы можем выразить через подобие треугольников ВСЕ и АСР. Так как треугольники ВСЕ и АСР подобны, то  (в подобных треугольниках все сходственные элементы находятся в одном отношении, ВК и КЕ – проекции сторон ВС и СЕ на сторону ВЕ в треугольнике ВСЕ, MP, AM – аналогичные проекции в треугольнике АСР). Т. е. 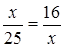. Далее, решая полученное уравнение, мы устанавливаем числовые данные.

В данной задаче мы установили геометрический образ неизвестного благодаря геометрическому образу точки встречи. Интерпретировать эти геометрические образы ученики умеют с предыдущего этапа. Тем не менее, работа по их выделению его неотъемлемая часть, существенно новым для данного этапа является геометрическое получение равенства 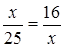. Важно, чтобы ученики поняли, что данный результат является обоснованным, что данное отношение следует из условия задачи, а использование графической модели лишь промежуточный шаг, который дает верные результаты вследствие изоморфности условию. Для этого их можно попросить ответить, опираясь на графическую модель, на следующие вопросы: что можно сказать о скоростях пешеходов, какие параметры в данной графической модели можно менять, какие остаются неизменными и сохраняется ли при этом полученное отношение? Для того, чтобы обосновать, что полученное в ходе решения уравнение является следствием условия задачи, а не данной графической модели можно привести решение, не опирающиеся на данную модель. Пусть скорость первого пешехода будет , а скорость второго пешехода будет , и пусть время, затраченное обоими до момента встречи, будет равно t . Тогда путь, пройденный первым до момента встречи, будет , а вторым ­ . Заметим, что второму осталось пройти до конца пути столько же, сколько прошел первый до момента встречи, а первому ­– сколько прошел второй. Значит 1) , а 2) , поделим первое равенство на второе, получим искомое отношение.

При таком подходе каждый раз, в отличие от способа, где используется графическая модель, нужно проводить различные рассуждения: в данном случае нужно догадаться и обосновать равенства 1) и 2) и уже потом перейти к отношению, в то время как из графической модели данное отношение непосредственно следует. Стоит показать ученикам данные подходы для обоснования независимости полученного решения и преимуществ первого подхода.

Далее следует перейти к задачам второго типа, давая их как задачи, в которых геометрия их графических моделей играет вспомогательную, а не основную роль. Четкого критерия для того, чтобы отличить данные задачи от задач первого типа дать нельзя, тем не менее, ученики должны понимать разницу между ними. Основной довод в пользу того, что задача второго типа состоит в том, что геометрический образ искомой величины не выражается явно (из подобия или равенства фигур) при помощи геометрии. Но, во всяком случае, геометрия графической модели такова, что величина геометрического образа искомого однозначно из нее определяется, в случае если условия задачи являются полными. И хотя мы ее не ищем при помощи геометрии, но имеющаяся в графической модели информационная картина такова, что содержит все сведения для перехода к математической модели. Все навыки для получения этих сведений ученики имеют, тем более они отработаны в процессе решения задач первого типа. Нужно переходить непосредственно к анализу данных задач. Приведем пример анализа подобной задачи.

Задача 7.Из пунктов А и В одновременно навстречу друг другу отправились велосипедист и пешеход. Велосипедист в пункте В повернул назад и через час после начала движения встретил пешехода. Доехав до А, снова повернул назад и встретил пешехода через 40 минут после первой встречи. Определить время, затраченное пешеходом на весь путь.

Так как в условиях не дана ни одна величина размерности длины, то весь путь можно принять за единицу. Обозначим через  скорость пешехода, через – скорость велосипедиста. Приведем для наглядности иллюстрацию (рис. 7), но в этой задаче она будет играть вспомогательную роль. Составим уравнения, используя при этом графическую модель. За час, прошедший до первой встречи, пешеход и велосипедист вместе прошли удвоенный путь от А до В, что непосредственно видно из иллюстрации, поэтому . За  часа до второй встречи велосипедист прошел на удвоенный путь больше, чем пешеход, поэтому

.

Решая систему

,

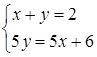получаем . Это означает, что за час пешеход проходит 0,4 всего пути, а на весь путь он затратит 2,5 часа.

В данной задаче нам требуется найти длину отрезка AD . Она не выражается из подобия или равенства треугольников, но, как видно, имеет определенное значение. Все уравнения, полученные в ходе решения задачи, не являются следствиями каких-либо геометрических соображений, но имеющаяся в графической модели информация наглядно иллюстрирует логику построения математической модели данной задачи. Таким образом, графическая модель отвечает на вопросы: что дано и что требуется найти? Она помогает переформулировать вопросы так, что от них непосредственно можно перейти к уравнению, например, из того факта, что велосипедист и пешеход первый раз встретились через час после начала движения, с помощью иллюстрации достаточно просто получить, что к моменту первой встречи они вместе прошли удвоенный путь, что непосредственно приводит к уравнению.

В задачах второго типа ориентировочная основа действий менее содержательна по сравнению с ней для задач первого типа. Тем не менее, умения строить графическую модель, интерпретировать ее, формулировать факты, заложенные в ней в виде, удобном для составления уравнений, являются основополагающими для успешного решения и достигаются в процессе решения системы задач [12, 15].

Как показывает опытное преподавание, использование данного способа визуализации для обучения решению задач на прямолинейное равномерное движение, является эффективным средством. Его эффективность обуславливается следующими причинами: данный способ естественно приводит к математической модели, данный способ отражает структуру задачи, соответствует формуле наглядности, данной Болтянским. Поясним приведенные аргументы. Естественность получения математической модели заключается в том, что мы получаем её непосредственно из графической модели. Например, во втором способе решения задачи 6 непонятно, почему мы вводим в качестве переменных скорости движения пешеходов, почему рассматриваем именно равенства 1) и 2), и, наконец, деление одного равенства на другое является также достаточно искусственным шагом, в то время как из графической модели уравнение следует естественным образом. Данный способ визуализации отражает структуру задачи, т.е. взаимосвязи между данными задачи, это помогает увидеть общее в разных, на первый взгляд, задачах, что, в свою очередь, формирует представление о математическом моделировании в целом.