Методика построения визуальных моделей при обучении решению текстовых задач

 

В этом параграфе рассмотрим методы визуализации тестовых задач. В качестве методов визуализации рассмотрим использование линейных и двумерных диаграмм, а так же применение графиков линейной функции. Данные методы визуализации основаны на геометрических свойствах фигур (прямоугольников, треугольников, отрезков) и свойствах операций над ними. При решении задач с использованием данного вида визуализации выделяют следующие три этапа: построение визуальной модели, то есть перевод задачи на геометрический язык, решение получившейся геометрической задачи, перевод задачи с геометрического языка на естественный. Для обучения построению и работы с визуальными моделями используется указанная выше трехэтапная методика, роль и значение этапов которой варьируется в зависимости от сложности конкретного способа визуализации. Задачи в этом параграфе выделяются не по содержанию сюжета, а по соответствию тому методу визуализации, который к ним применим.

Линейные диаграммы используются преимущественно в тех задачах, в которых искомое находится в зависимости от данных, выразимой с помощью арифметических операций сложения (вычитания) и умножения (деления). В курсе алгебры представлены два основных вида задач (текстовых), решаемых с помощью линейных диаграмм: 1) задачи, в которых даны отношения значений величин и отражена одна ситуация в данный момент времени; 2) задачи, в которых даны отношения значений величин и отражены две ситуации – первоначальная и конечная. При решении задач первого вида линейная диаграмма выступает в качестве статической геометрической модели, то есть в процессе решения задачи она не изменяется и выполняет только иллюстративную функцию. Наибольший интерес с точки зрения использования линейных диаграмм в курсе алгебры представляют задачи второго вида. Построение линейной диаграммы при решении этих задач проходит в два приема: в начале строится диаграмма, отражающая первоначальное (конечное) состояние объектов, а затем согласно условию она изменяется таким образом, чтобы вновь полученное изображение (диаграмма) отражала конечное (первоначальное) состояние объектов. Изменение построенной диаграммы осуществляется путем действий над отрезками (сложения и умножения на число) [9].

Так как роль первого этапа методики обучения работе с визуальными моделями состоит в том, чтобы выделить основные понятия и объекты, участвующие в построении модели, то, в данном случае необходимость в нем отпадает. Связанно это с тем, что для построения и работы с линейными диаграммами используются отрезки и операции с ними, что изучается на протяжении всего школьного курса математики.

Второй и третий этапы не нужно явно отделять друг от друга: обучение моделированию происходит непосредственно в процессе решения задач, но в начале нужно провести методическую работу для формирования умений построения визуальной модели. Эта работа заключается в акцентировании внимания на существенных сторонах в построении визуальной модели, которые отражают суть задачи. А именно, рассмотреть случаи, в которых длина отрезка может выбираться произвольно, и случаи когда длина отрезка зависит от каких-то условий. Необходимо также провести различие между задачами первого и второго вида. Для задач второго вида показать, что мы идем от одного состояния к другому, при этом посредством арифметических операций над отрезками, соответствующих условию, получаем из первоначальной диаграммы другую, иллюстрирующую данное состояние. Приведем пример.

Задача 1. На одном овощехранилище было втрое больше картофеля, чем на другом. С первого вывезли 450 кг картофеля, а на второе привезли 120 кг картофеля, после чего на обоих овощехранилищах картофеля стало поровну. Сколько килограмм картофеля было на каждом овощехранилище первоначально?

Как было отмечено выше решение задачи при использовании диаграмм, осуществляется в три этапа.

Первый этап. После прочтения задачи учащиеся отвечают на вопросы:

1. Сколько ситуаций рассматривается в задаче? (Две: первоначальная и конечная).

2. С какой ситуации следует начать построение линейной диаграммы? (Можно начать с первой ситуации и перейти от нее ко второй, а можно сначала построить диаграмму конечной ситуации и перейти от нее к первоначальной. Рассмотрим первый вариант).

3. Что будет представлять собой первоначальная диаграмма? (Два отрезка, один из которых втрое больше другого). После этого ученики строят первоначальную диаграмму, далее рассуждения продолжаются.

4. Как перейти на диаграмме от первой ситуации ко второй? (Надо из первого отрезка вычесть второй условно изображающий 450 кг, а ко второму прибавить отрезок изображающий 120 кг).

5.

C

Произвольно ли берутся отрезки изображающие 120 и 450 килограмм? (Нет, следует учитывать, что вновь полученные отрезки должны быть равны, так как на обоих хранилищах картофеля стало поровну).

Выполнив действия с отрезками, учащиеся получают диаграмму конечной ситуации. Первый этап работы над задачей заканчивается обозначением отрезков и оформлением записей на чертеже (рис.1).

Второй этап. Построенная линейная диаграмма превращает алгебраическую задачу в геометрическую, решение которой основано на использовании свойств длины отрезка. Ответ можно получить арифметически, не составляя уравнение, иногда его можно «усмотреть» на чертеже. С помощью диаграммы можно составлять различные уравнения к задаче, то есть решать её разными способами.

Третий этап. Перевод с геометрического языка на естественный осуществляется автоматически, в результате переноса терминологии. В начале следует сделать подробную запись с указанием того, что обозначает каждый отрезок. Постепенно можно переходить к краткой записи, так как некоторые факты видны на чертеже.

На мотивационном этапе формирования геометрического метода основанного на использовании линейных диаграмм целесообразно предлагать решить задачу двумя методами: алгебраическим и геометрическим. При этом следует подбирать задачу таким образом, чтобы её решение с помощью линейной диаграммы было более рациональным по сравнению с решением без чертежа.

Далее следует рассмотреть класс задач, для которых применим данный метод визуализации. При этом сюжеты задач должны быть разными, для того чтобы данный метод не ассоциировался с каким-то определенным видом сюжетных задач. При этом сложность задач, сложность построения модели должна повышаться. Нужно также указывать на модели различных сюжетных задач, в случае если они сходны, так как это формирует представление об универсальности данного метода, и вообще о моделировании как общего математического метода [12, 21].

Данный метод визуализации применим для относительно простых задач, тем не менее, его значимость достаточно высока. Он обогащает арсенал средств, которыми может пользоваться ученик при решении задач, а задачи, в которых данный метод применим, довольно часто возникают в качестве подзадачи на этапе анализа при решении более сложных задач. Часто такие задачи бывают на всевозможных математических турнирах, где требуется их решить за минимальное время. Например: «Кирпич весит 2 кг и еще пол кирпича. Сколько весит кирпич?» или «"То" да "это", да половина "того" да "этого"– сколько это будет процентов от трех четвертей "того" да "этого"?». Данный метод может оказать в подобном случае существенную помощь. Кроме того, данный метод является эффективным средством как при обучении решению задач на проценты, так и при обучении понятию процента как части от целого.

Линейные диаграммы могут использоваться на разных этапах решения задачи. При анализе текста она помогает учащимся лучше понять смысл задачи, рассматриваемые в ней отношения, при поиске способа решения – составить уравнение или арифметическое выражение. На этапе анализа решения задачи можно найти другое (иногда более рациональное) решение. Оно может использоваться для проверки ответа, полученного алгебраическим способом.

В задачах, где одна из рассматриваемых величин является произведением двух других, можно для наглядности представить такое произведение в виде площади прямоугольника, то есть в виде двумерной диаграммы. Двумерная диаграмма может состоять из одного или нескольких прямоугольников.

Подготовительная работа к моделированию текстовых задач в данном случае, как и при использовании линейных диаграмм не требуется, так как используемые объекты и методы работы с ними ученикам достаточно хорошо известны и не представляют особой сложности.

Второй этап в методике обучения использованию двумерных диаграмм можно реализовать, опираясь на линейные диаграммы. Лучше всего перейти к моделированию тех задач, которые предварительно решены алгебраическим методом. Это связанно с тем, что ученики знают структуру задачи, установлены связи между данными и искомым, что делает построение модели более естественным. Кроме того, такой подход позволяет сравнить два способа решения задачи.

Перед построением геометрической модели, нужно установить связь геометрических преставлений в виде двумерных диаграмм с геометрическими представлениями в виде линейных диаграмм. Для этого, необходимо заметить учащимся, что в случае использования линейных диаграмм отрезками изображались значения одной и той же величины. Эти отрезки располагались на параллельных прямых. В задачах, где рассматривается произведение двух величин, отрезками будем изображать значения двух разных величин и отрезки будем располагать на двух перпендикулярных прямых так, чтобы они были смежными сторонами прямоугольника. Тогда площадь прямоугольника будет соответствовать произведению этих величин, а полученное изображение будем называть двумерной диаграммой. Приведем пример.

Задача 2. Моторная лодка, скорость которой в стоячей воде 15 км/ч, прошла по течению реки 35 км и против течения 25 км. На путь по течению реки она затратила столько же времени как на путь против течения. Какова скорость течения реки.

Алгебраический метод приводит к уравнению:

,

где  – скорость реки. Решив уравнение, находим .

Рассмотрим геометрический метод. Так как в данной задаче рассматривается равномерное движение, то пройденный лодкой путь можно представить в виде произведения скорости и времени движения.

Пусть сторона АВ прямоугольника АВС D изображает скорость лодки по течению реки (рис. 2). Тогда AD будет изображать время движения лодки по течению реки. Если обозначить через  скорость течения реки, а через 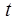 – время движения лодки по течению реки, то  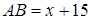и .

Площадь прямоугольника АВС D (S₁)будет соответствовать пути пройденному лодкой по течению реки: .

Далее следует предоставить учащимся самим построить двумерную диаграмму движения лодки против течения реки. Необходимо акцентировать их внимание на следующих моментах: прямоугольники нужно изображать вместе, чтобы они составляли одну фигуру, причем высоты этих прямоугольников должны быть равны, так как лодка двигалась одинаковое время по течению и против течения реки, целесообразнее высоту прямоугольников, изображающую время, сделать общей, тогда получаем фигуру в виде прямоугольника, площадь которого легко найти.

Далее продолжаем решение. Пусть отрезок BE изображает скорость лодки против течения реки (BE берем меньше АВ), тогда отрезок EF изображает время движения лодки против течения реки: .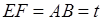

Площадь прямоугольника BEFC соответствует пути пройденному протии течения реки: . Площадь прямоугольника ABFC определяет весь путь пройденный лодкой: .

В то же время, , , 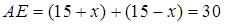, тогда имеем: 60=30 , , 35:2 = 17,5 – скорость движения лодки по течению,  17,5 – 15 = 2,5 – скорость течения реки.

Использование двумерных диаграмм в курсе алгебры опирается на следующую теорему: если через произвольную точку E диагонали AC прямоугольника ABCD проведены прямые FM и HK параллельные соответственно AB и AD, образовавшиеся при этом прямоугольники HBME и FEKD будут равновелики, прямоугольники ABMF и AHKD тоже равновелики, кроме того отрезки FH, DB и KM параллельны.

Приведем пример решения задачи с использованием данной теоремы.

Задача 3. Один наборщик работал над выполнением заказа 9 часов. После чего закончить работу было поручено второму наборщику, который закончил работу за 4 часа 48 минут. Если бы оба наборщика работали вместе, то они выполнили бы работу за 6 часов 40 минут. За сколько времени каждый выполнил бы работу, работая отдельно?

Работа, выполненная наборщиком, равна произведению его часовой выработки на число выработанных им часов и, следовательно, может быть представлена площадью прямоугольника.

Проведем горизонтальный отрезок (рис. 3) AB произвольной длины (почему мы можем длину выбирать произвольно?), пусть он изображает часовую выработку обоих наборщиков вместе. Перпендикулярно ему проведем два луча AA₁ и BB₁. Единичный отрезок будет обозначать один час работы. Отметим время на каждом из этих лучей, начиная от нуля. На луче АА₁отметим точку М, указывающую 6 часов 40 минут и проведем отрезок МР. Площадь прямоугольника АМРВ обозначает количество всей работы. Но эта работа выполнялась наборщиками поочередно, поэтому теперь следует построить два прямоугольника изображающих соответственно работу каждого наборщика отдельно. Оба прямоугольника вместе должны быть равновелики прямоугольнику АМРВ. Известны высоты этих прямоугольников (чему они равны?). Сумма оснований искомых прямоугольников должна составлять отрезок AB (почему?),так как часовая выработка при совместной работе двух наборщиков равна сумме часовых выработок каждого из них.

Задача сводится к разбиению отрезка AB на два таких отрезка АС и СВ, чтобы сумма площадей двух прямоугольников ACLK и CBRQ была равна площади прямоугольника АМРВ.

На луче BB₁ отметим точку Т (ВТ=АК) изображающую 9 часов, на луче АА₁ отметим точку S (AS = BR) изображающую 4 часа 48 минут. Проведем отрезок ST. Точка N пересечения отрезков ST и МР определяет размеры MN и NP оснований искомых прямоугольников. Найденные прямоугольники ACLK и CBRQ равновелики прямоугольнику АМРВ.

Для того чтобы получить ответ задачи достаточно провести прямую AN до пересечения в точке D с лучом BB₁, и прямую BN до пересечения в точке Е с лучом АА₁. Длины отрезков будут искомыми величинами. Ответ 12 и 15.

Если построения выполнить на миллиметровой бумаге, взяв 1 мм за час, то данный ответ можно считать обоснованным. Если чертеж выполняется от руки не на миллиметровой бумаге и без масштаба, то для получения ответа требовались бы вычисления использующие подобие трех пар треугольников: SMN и TPN, ADB и ANC, BEA и BNC . Откуда MN : MP = MS : PT . Но

MS = AM – AS =6 ч 40 мин – 4ч 48 мин = 112 мин,

PT = BT – PB = 9ч – 6ч 40 мин =140 мин.

Следовательно, MN : MP = 4:5. Далее BD : CN = AB : AC = MN : MP = 9:4. Отсюда BD = =  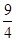6 ч 40 мин =15 ч. Аналогично, АЕ = 12 часов.

Во всяком случае, решение мы получаем благодаря решению геометрической задачи.

Решение задач с помощью изложенного метода опирается на достаточно сложный геометрический материал. Но методика обучения данному виду геометрического моделирования задач не включает его в себя. Сама методика предполагает формирование у учащихся представлений о связи двумерных диаграмм с величинами, которые можно представить в виде произведения двух других (например, путь, скорость и время), и умений работать с диаграммой. Все это формируется в процессе моделирования уже разобранных (решенных алгебраическим методом) задач с опорой на соответствующий материал о линейных диаграммах. Весь геометрический материал необходимый для работы с диаграммами представляет собой приведенную выше теорему, и три построения, которые обосновываются с помощью данной теоремы. Например, в задаче 3 при нахождении двух прямоугольников равновеликих данному используется такое построение. Весь геометрический материал можно изучить в курсе геометрии в теме «Площади». Задачи для обучения моделированию с помощью двумерных диаграмм нужно подобрать так, чтобы среди них были модели, использующие все построения. В начале задачи должны быть простыми, не использующими построения, например, задача 1 и усложнятся в последствии.

С помощью двумерных диаграмм можно составить разные уравнения одной и той же задачи, это помогает найти более рациональный путь решения. Кроме того, она позволяет наглядным образом обосновывать полученные уравнения, позволяет наглядно представить процесс, описанный в задаче.

Как мы видели на примере задачи 3, её, при выполнении соответствующих требований, можно решить благодаря только геометрическим построениям. Существует класс задач на совместную работу, которые можно решить благодаря только построениям в системе координат. Приведем пример одной из таких задач.

Задача 4. Бассейн заполняется водой через одну трубу за 4 часа, а через другую вода может вытечь за 6 часов. За сколько времени наполнится бассейн при одновременном действии обоих труб?

Рассмотрим прямоугольную систему координат  (рис. 4). Пусть отрезок OD изображает объем бассейна, тогда отрезок ОА является графиком наполнения бассейна через первую трубу, отрезок ОВ графиком вытекания воды из бассейна через вторую трубу. Графиками являются отрезки, так как объем воды, протекающий через трубу, прямо пропорционален времени. За 4 часа первая труба одна наполнит весь бассейн. Через вторую трубу за это время вытечет воды объемом, изображением которого служит отрезок МК. Объем воды, оставшейся в бассейне изображается отрезком АК=АМ – МК. Отложим отрезок МР = АК, проведем через точки О и Р прямую до пересечения С с прямой, изображающей объем. Тогда ОС является графиком наполнения бассейна при одновременном действии двух труб. Из рисунка видно, что через 12 часов бассейн наполнится. Условия, при которых мы можем принимать результат решения задачи без дополнительной проверки, описаны ниже и требуют отдельного рассмотрения с учениками в процессе обучения решению задач подобными методами.

То, что графиками указанных зависимостей будут отрезки обоснованно в ходе решения задачи. Принцип построения данных графиков также прост, для этого нужно соединить начало координат и точку, которая соответствует времени выполнения работы. Основной вопрос как построить результирующий график и почему он соответствует верному результату. Ответ на этот вопрос раскрывает смысл метода решения задач данным способом. Для приведенной выше задачи нужно построить отрезок МР, который равен объему совместной работы труб, в то время как первая труба заполнит объем соответствующий отрезку АК, через вторую трубу вытечет объем соответствующий МК. По построению МР=АМ – МК. Значит график совместной работы будет проходить через точку Р так как графиком является отрезок проходящий через начало координат, то теперь мы можем однозначно его построить.

Для того, чтобы решать задачи с помощью данного метода, нужно уметь еще строить результирующий график совместной работы. Работа может выполняться ее участниками в различном направлении (как «трубы» в предыдущей задачи) или в одном направлении.

Приведем пример задачи, где работа выполняется в одном направлении.

Задача 5. Ванна заполняется холодной водой за 6 минут 40 секунд, горячей – за 8 минут. Кроме того, если из полной ванны вынуть пробку, вода вытечет за 13 минут 20 секунд. Сколько времени понадобится, чтобы наполнить ванну полностью, при условии, что открыты оба крана, но ванна не заткнута пробкой?

Пусть отрезок OD (рис. 5) изображает весь объем, тогда отрезок OC график работы крана с холодной водой, отрезок DB – с горячей. Пусть M точка пересечения этих графиков, из рисунка видно, что к моменту времени соответствующему точке M, оба крана, работая совместно, выполнят весь объем работы. Тогда проведем отрезок BK через точку M перпендикулярно оси абсцисс, так как к моменту времени B (или К) весь объем работы будет выполнен, то отрезок OB (или DK) будет графиком совместной работы. OP график, соответствующий работе по вытеканию воды. Из графиков OB и OP, с помощью метода описанного в предыдущей задаче получаем результирующий график. Из рисунка видно, что ванна заполнится через 5 минут.

Рис.5

Данный метод дает точный ответ, не требующий вычислений только в том случае, если выбран масштаб и все данные и ответ к задаче являются числами, находящимися в точках которые соответствуют целому числу единичных отрезков.

Данный метод используется для решения достаточно узкого класса задач, в которых дано время, затрачиваемое на работу каждым субъектом в отдельности, и требуется найти их общую производительность. Алгоритм арифметического решения этих задач прост: выражается количество работы, выполняемой за час одним субъектом, затем результаты всех складываются – это будет общая производительность. Графическая модель помогает представить наглядно решение задачи, кроме того, она подводит к графическому методу решения более сложных задач, который будет рассмотрен в следующем параграфе.