Занятие №8. Теорема сложения вероятностей.

Из четырех теорем о сложении вероятностей (для двух несовместных событий, для n несовместных событий (обобщение), для событий, образующих полную группу и для противоположных событий) практический интерес для слушателей курса представляют лишь две теоремы: первая и третья. Обе они часто используются при решении вероятностных задач, и поэтому их следует подробно с доказательством рассмотреть на занятии. Теорему о противоположных событиях (как частный случай третьей теоремы) можно поручить рассказать одному из учащихся.

Теорема 1. Пусть события А и В – несовместные, причем вероятности этих событий известны. Тогда вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р(А+В)=Р(А)+Р(В).

Доказательство. Введем обозначения: n – общее число возможных элементарных исходов испытания; m₁ – общее число исходов, благоприятствующих событию А; m₂ – общее число исходов, благоприятствующих событию В.

Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m₁+m₂. Следовательно,

Р(А+В)= .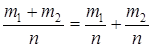

Приняв во внимание, что 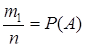 и 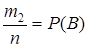, окончательно получим

Р(А+В)=Р(А)+Р(В).

Теорема 2. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р(А₁+А₂+…+А_n)=Р(А₁)+Р(А₂)+…+Р(А_n).

Теорема 3. Сумма вероятностей событий А₁, А₂, …, А_n, образующих полную группу, равна 1:

Р(А₁)+Р(А₂)+…+Р(А_n)=1.

Доказательство. Так как появление одного из событий полной группы достоверно, а вероятность достоверного события равна единице, то

Р(А₁+А₂+…+А_n)=1. (*)

Любые два события полной группы несовместны, поэтому можно применить теорему сложения:

Р(А₁+А₂+…+А_n)=Р(А₁)+Р(А₂)+…+Р(А_n). (**)

Сравнивая (*) и (**), получим

Р(А₁)+Р(А₂)+…+Р(А_n)=1.

Теорема 4. Сумма вероятностей противоположных событий равна 1:

Р(А)+Р( 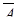)=1.

Задачи:

1. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.

2. На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем 5 из них в переплете. Библиотекарь берет наудачу три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете. (Решить двумя способами: с помощью 1 и 4 теорем).

3. Производится бомбометание по трем складам боеприпасов, причем сбрасывается одна бомба. Вероятность попадания в первый склад 0,01; во второй 0,008; в третий 0,025. При попадании в один из складов взрываются все три. Найти вероятность того, что склады будут взорваны.

4. Круговая мишень состоит из трех зон: I, II, III. Вероятность попадания в первую зону при одном выстреле 0,15, во вторую 0,23, в третью 0,17. найти вероятность промаха.