Расстояние между точками на плоскости

Пусть на плоскости заданы точки М₁(x₁; y₁) и М₂(x₂; y₂), найти расстояние между ними, т.е. найти

 

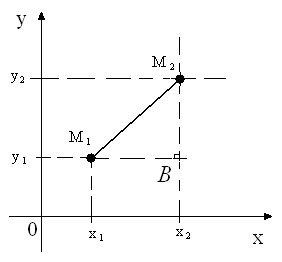
Рис.4

 

Т.к. треугольник М₁М₂В прямоугольный, то из теоремы Пифагора следует, что

 

,

а т.к.

 

то окончательно получаем, что

 

Полярные координаты и их связь с декартовыми координатами

Пусть точка М на плоскости задана так, что (см. Рис.5)

 

Рис.5

 

Где точка  0 – полюс, луч 0А – полярная ось,  - полярный радиус, φ – полярный угол (полярный угол, как и во всей математике отсчитывается против часовой стрелки от положительного направления оси – в нашем случае от направления полярной оси).

Если совместить две системы координат (полярную и ПДСК) так, чтобы: они имели общее начало – точку 0, положительное направление полярной оси совпало с положительным направлением оси 0x (см. Рис.6), то будет понятно – как связаны ПДСК и полярная системы координат.

Рис.6

 

 

Для большего удобства переходов ПДСК-полярная и обратно сформируем таблицу.

Таблица взаимосвязи ПДСК и полярной системы координат

Выражение декартовых координат через полярные	Выражение полярных координат через декартовы

 

Пример 2 (нахожденние расстояния между двумя точками)

 

Найти расстояние между точками

Решение:

Координаты точек заданы в полярных координатах, а выражение для нахождения получено для точек, заданных в ПДСК, а потому, прежде всего, необходимо выразить координаты точек в ПДСК.

Из таблицы взаимосвязи полярных и декартовых координат получаем, что для точки

,

или, координаты точки М в ПДСК - .

Аналогично находим и координаты точки N:

,

или, координаты точки N в ПДСК - .

А вот теперь, окончательно, используя результат «расстояние между двумя точками на плоскости», получаем, что

 

Вычисление площади произвольного треугольника в ПДСК

Пусть в ПДСК задан произвольный треугольник ABC: А(x₁, y₁), B(x₂, y₂) и C(x₃, y₃), тогда площадь треугольника S_ABC определяется выражением

 

 

Поскольку точки могут быть пронумерованы в произвольном порядке, знак определителя может изменяться. В силу чего существует правило: результат берется по абсолютной величине (по модулю).

Деление отрезка в данном отношении

Прежде всего, о смысле выражения «деление отрезка в данном отношении».

Пусть точка В делит отрезок А₁А₂ (см. Рис.7)

 

Рис.7

 

Тогда , т.е., если , то . Но если отрезок «прочитать» по-другому: не А₁А₂, а А₂А₁, то

Откуда важный вывод: при разбиении отрезка в отношении λ, важно как устроена дробь

 

т.е. важно, в каком направлении читается отрезок: А₁А₂, или А₂А₁.

Координаты точки, делящей отрезок в данном отношении

Пусть точка В(x; y) делит отрезок А₁А₂ [A₁(x₁; y₁) и A₂(x₂; y₂)] в отношении λ, тогда

.

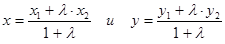Следствие: если точка В делит отрезок А₁А₂ пополам, т.е. λ = 1 (почему?), то

.