 |
Главная |
Пример 25 (свободные векторы)
|
из
5.00
|
На рисунке 26 представлены три вектора. Один из них – вектор  уже был рассмотрен в Примере 24.
уже был рассмотрен в Примере 24.

Рис.26
Не трудно убедиться в том, что

Основные арифметические действия над векторами
Здесь и далее предполагается, что векторы  заданы в координатной форме
заданы в координатной форме

Длина вектора
Длина вектора  определяется выражением
определяется выражением

Скалярное произведение (координатная форма)

Угол между векторами
Если φ – угол между векторами  , то
, то

Условие ортогональности векторов
Два вектора  ортогональны при условии равенства нулю их скалярного произведения
ортогональны при условии равенства нулю их скалярного произведения

Сумма (разность) векторов

Векторное произведение векторов
Векторным произведением векторов  называется вектор, обозначаемый символом
называется вектор, обозначаемый символом  ( или
( или  ), который определяется условиями
), который определяется условиями
1.  , где φ – угол между векторами
, где φ – угол между векторами  ;
;
2. вектор  такой, что
такой, что  одновременно;
одновременно;
3. вектор  ориентирован по отношению к сомножителям по правилу буравчика.
ориентирован по отношению к сомножителям по правилу буравчика.
Правило буравчика
Вектор  , как результат векторного произведения
, как результат векторного произведения  ориентирован по отношению к сомножителям так же, как координатная ось Oz по отношению к осям Ox и Oy (cм. Рис. 27). Т.е., при вращении от первого сомножителя ко второму буравчик ввинчивается в направлении вектора
ориентирован по отношению к сомножителям так же, как координатная ось Oz по отношению к осям Ox и Oy (cм. Рис. 27). Т.е., при вращении от первого сомножителя ко второму буравчик ввинчивается в направлении вектора  .
.

Рис.27
Условие коллинеарности векторов
Если векторы  коллинеарны (лежат на одной прямой или на параллельных прямых) т.е. угол между ними или 0, или 1800, то их векторное произведение равно нулю
коллинеарны (лежат на одной прямой или на параллельных прямых) т.е. угол между ними или 0, или 1800, то их векторное произведение равно нулю

Геометрический смысл векторного произведения
Если векторы  приведены к общему началу (что параллельным переносом возможно сделать всегда, поскольку мы работаем только со свободными векторами), то длина вектора
приведены к общему началу (что параллельным переносом возможно сделать всегда, поскольку мы работаем только со свободными векторами), то длина вектора  равна площади параллелограмма, построенного на перемножаемых векторах (см.Рис.28).
равна площади параллелограмма, построенного на перемножаемых векторах (см.Рис.28).

Рис.28
Свойства векторного произведения
1. Свойство антикоммутативности
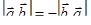
2. Свойство ассоциативности по отношению к скалярному множителю λ


4. Распределительное свойство относительно операции сложения

Пример 26 (раскрытие скобок в выражении с векторами)
Раскрыть скобки в выражении

Решение

Пример 27 (вычисление площади параллелограмма)
Вычислить площадь параллелограмма, построенного на векторах  и
и  , если
, если 
 ;
;
 ;
;

Решение
Прежде всего, площадь параллелограмма, построенного на векторах  и
и  , определяется как
, определяется как
 .
.
Т.е. найдем векторное произведение векторов c и d, а потом длина полученного вектора численно будет равна искомой площади параллелограмма.
Шаг 1
Ищем векторное произведение, при этом активно используем свойства векторного произведения



Шаг 2
Ищем, собственно площадь 
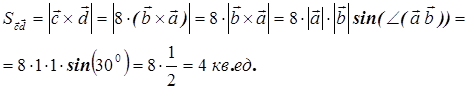
|
из
5.00
|
Обсуждение в статье: Пример 25 (свободные векторы) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

