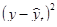Методы обработки динамики урожайности картофеля для выявления основной тенденции

Год	Урожай-ность картофе-ля, ц с 1 га   у	Пер-вые раз-ности	Вторые разности	Метод укрупнения периодов (3–х кв.)			Метод средней скользящей (3-х кв.)			Метод аналитического выравнивания по уравнению прямой, параболы (расчетные величины для определения параметров)			Теоре-тичес-кий уровень уро-жай-ности, рассчи-танный по уравнению прямой		Теорети-ческий уровень урожай-ности, рассчи-танный по уравнению параболы
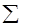
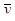
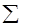
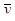
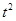
								t		t4	уt	yt2
1996	76,40	-	-	-	-	264,6	88,2	-7	49	2401	-534,8	3743,6	86,74	107,00	79,82	11,68
1997	90,10	13,70	-	264,6	88,2	283,8	94,6	-5	25	625	-450,5	2252,5	87,11	8,94	82,73	54,29
1998	98,10	8,00	-5,70	-	-	273,6	91,2	-3	9	81	-294,3	882,9	87,48	112,87	85,09	169,16
1999	95,60	-2,50	-10,50	-	-	263,8	87,9	-1	1	1	-95,6	95,6	88,84	60,19	86,90	75,62
2000	79,90	-15,70	-13,20	263,8	87,9	252,9	84,3	1	1	1	79,9	79,9	88,21	69,02	88,16	68,26
2001	88,30	8,40	24,10	-	-	264,1	88,0	3	9	81	264,9	794,7	88,57	0,08	88,87	0,32
2002	84,70	-3,60	-12,00	-	-	-	-	5	25	625	423,5	2117,5	88,94	17,98	89,02	18,68
2003	91,10	6,40	10,00	-	-	-	-	7	49	2401	637,7	4463,9	89,31	3,22	88,62	6,13
Итого	704,2	-	-	-	-	-	-	0	168	6216	30,8	14430,6	704,20	379,29	689,22	404,14

При затруднении выбора формы кривой, можно привести расчет наиболее часто используемых моделей для аналитического выравнивания. По полученным моделям для каждого периода (каждой даты) определяются теоретические уровни тренда, стандартная ошибка аппроксимации и коэффициент вариации (см. табл. 3.4.2).

На основании ряда динамики урожайности картофеля, для выявления общей тенденции использованы наиболее часто используемые методы: укрупнения периодов, средней скользящей, аналитического выравнивания [5, c. 23].

 Первые методы не позволяют выявить общую тенденцию (тренд) в данном динамическом ряду, поэтому наиболее прогрессивным методом является метод аналитического выравнивания.

Выявим модель тренда (уравнение прямой) для определения тенденции.

,    

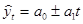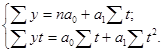
В нашем случае:

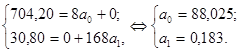
Значит модель тренда (уравнение прямой) для определения тенденции имеет следующий вид: .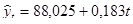

По данным уравнения видно, что наблюдается среднее увеличение урожайности картофеля по годам на 0,183 ц с 1 га.

Ошибка аппроксимации составляет 7,95 ц с 1 га, коэффициент вариации 9,03%:

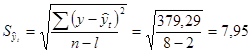 ц с 1 га; 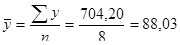ц с 1 га.

.

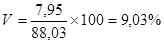Выявим модель тренда (уравнение параболы) для определения тенденции.

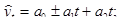
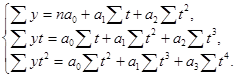
В нашем случае:

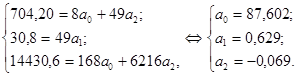
Значит, модель тренда (уравнение параболы) для определения тенденции будет иметь следующий вид: 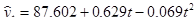. По данным уравнения тренда видно, что в среднем за год урожайность картофеля увеличивается на 0,629 ц с 1 га.

Ошибка аппроксимации составляет 8,99 ц с 1 га, коэффициент вариации 10,21%.

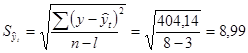 ц с 1 га; .

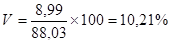Прямая лучше отражает тенденцию развития явления во времени, т.к. ошибка аппроксимации меньше.

 Так как коэффициент вариации не превышает 25%, следовательно данный динамический ряд устойчив и данную модель тренда можно использовать при прогнозировании.

Уравнение тренда применяют при прогнозировании, т.е. определения уровней ряда динамики за его пределами – метод экстраполяции. Прогноз может быть точечным (по уравнению тренда) или интервальным (с использованием ошибки аппроксимации) [5, c. 22].

При прогнозе следует определить:

- на основании какого числа уровней ряда динамики можно построить уравнение тренда;

- каким может быть горизонт прогнозирования (период упреждения).

Период прогнозирования не должен превышать 1/3 числа уровней, на основе который построено уравнение тренда.

Точечный прогноз:

Для 2004 г. - 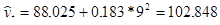 ц с 1 га.

Для 2005 г. - 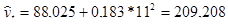 ц с 1 га.

Интервальный прогноз осуществляется по формуле (3.4.1):

(3.4.1)

Среднее квадратическое отклонение от тренда (ошибка аппроксимации):

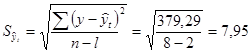 ц с 1 га

Теоретический уровень исчисляется так:

Для 2004 г. - 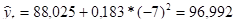 ц с 1 га.

Для 2005 г. - 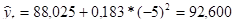 ц с 1 га.

 Р = 0,99, S_t =0,994, k =n-1=8-1=7, =>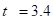

Интервальный прогноз:

Для 2004 г.: ,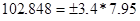

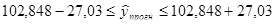
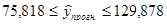
Для 2005 г.: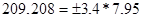

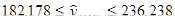
Значит интервальный прогноз урожайности картофеля для 2004 г 102,848 ц с 1 га находится в пределах от 75,818 ц с 1 га до 129,878 ц с 1 га. А для 2005 г интервальный прогноз урожайности картофеля 209,208 ц с 1 га находится в пределах от 182,178 ц с 1 га до 236,238 ц с 1 га.

Прогнозирование урожайности картофеля можно производить также при помощи полиномиальной функции различных порядков, экспоненциальной функции и степенной функции (Приложения 8,9,10,11,12,13).

Строится график зависимости между временным периодом и урожайностью картофеля, проводится линия тренда и на ее основании составляется прогноз.

Как видно из приводимых на графиках формул и величины достоверности аппроксимации наиболее значимым является прогноз по полиномиальной функции 6го порядка.

Тем не менее, такая функция дает достаточно достоверные результаты только при большом количестве периодов (не менее 5 периодов на каждый уровень полиномиальной функции). Следовательно, изменение урожайности картофеля для районов не является временным процессом.

3.5 Индексный метод анализа (применительно к данным группировок)

Если валовой сбор W рассматривается во взаимосвязи с площадью посева S урожайностью и приминает форму не простого, взятого изолированного показателя W, а составного W=S*y, то при сопоставлении его уровней используют индексный метод. Рассмотрим 

По группе однородных культур, продукция которых поддается суммированию, определяется агрегатный индекс валового сбора:

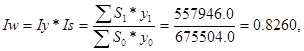 или 82,6%.

Поскольку изменение валового сбора, как и любого абсолютного результативного показателя, зависит от изменения числа единиц совокупности – носителей изучаемого признака (площадь посева S), значений признака (урожайность Y) и структуры совокупности (т.е. соотношения единиц с разным значением признака), - то агрегатный индекс в процессе анализа разлагается на индексы размера посевной площади Is, урожайности Iy и структуры посевных площадей Iстр [1, c. 86]. Практически используются две идентичные по результатам схемы разложения общего индекса:

,

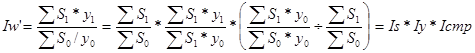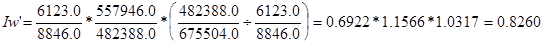, что составляет 82,6 %.

,

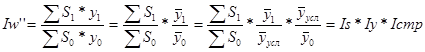где 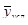 =  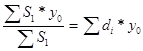- условная средняя урожайность при отчетной структуре посевов и базисной урожайности картофеля.

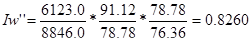(82,6%).

Разложение индексов можно видеть на примере анализа динамики валового сбора картофеля в хозяйствах по районам Удмуртской республике за 2003 г. (отчетный год) по сравнению с 1996 г. (базисный год), изображенном в таблице 3.5.1.

Таблица 3.5.1