Средние величины (в т.ч. структурные средние)

Среди показателей, применяемых в статистике, большое распространение получили средние величины. Средними величинами называют обобщающие показатели, выражающие типичные размеры и количественные соотношения общественных явлений.

В статистике применяются разные виды средних величин. Наиболее распространенными являются средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, степенные средние Выбор того или иного вида средней в каждом случае определяется характером изучаемых явлений и конкретных задач исследования. Признак, для которого исчисляется средняя величина, называется варьирующим или осередняемым признаком [10, c. 168].

Средняя арифметическая – самый распространенный вид средней, применяемый в социально-экономическом анализе.

Если имеется несколько различных индивидуальных величин одного и того же вида и надо исчислить среднюю, то необходимо найти сумму всех индивидуальных величин и поделить получаемую сумму на их число (простая средняя). Простая средняя арифметическая (`х_пр ) вычисляется в тех случаях, когда каждая из вариант встречается в изучаемом явлении один или одинаковое число раз. Она представляет собой результат деления суммы вариант (åх_i) на их число (n), т.е.

                                       `х_{ариф. пр} =(åх_i) / n.                             (1.3.1)

 Средняя арифметическая взвешенная (`х_взв) вычисляется в тех случаях, когда различные варианты встречаются в изучаемой совокупности неодинаковое число раз, что бывает значительно чаще. Ее определяют по формуле:

                                    `х _{ариф взв}= (åх_i*f_i) / åf_i,                          (1.3.2)

где f – частоты (веса).

Средняя гармоническая служит для обобщения обратных значений варьирующего признака. Этим она отличается от средней арифметической. Различают также среднюю гармоническую простую и взвешенную. Средняя гармоническая простая вычисляется по формуле:

                                                                                 (1.3.3)

где n- число вариант (х_i).

Средняя гармоническая взвешенная:

                                     `х_{гарм взв}=åm/å(m/х_i),                          (1.3.4)

где m= fх.

Средняя геометрическая равна корню степени п из произведения коэффициентов роста, характеризующих отношение величины каждого последующего периода к величине предыдущего, т.е.:

                                                                               (1.3.5)

Средняя квадратическая. В тех случаях, когда осреднению подлежат величины, выраженные в виде квадратных функций, применяется средняя квадратическая. Так, средние диаметры колес, труб, стволов, средние стороны квадратов и др. определяются при помощи средней квадратической.

Средняя квадратическая простая рассчитывается путем извлечения квадратного корня их частного от деления суммы квадратов отдельных значений признака на их число:

                               =                      (1.3.6)

Средняя квадратическая взвешенная равна:

                                                                                         (1.3.7)

где f- веса.

Степенные средние. Рассмотренные выше средние величины могут быть представлены в форме некоторой системы величин, выделенных из степенной средней вида:

                                                                                            (1.3.8)

где х - индивидуальные значения признака;

n – число единиц изучаемой совокупности;

k - показатель степени средней.

Придавая показателю степени средней различные целые значения, получим отдельные виды степенных средних: k=1 – среднюю арифметическую, k=-1 – среднюю гармоническую, k=0 – среднюю геометрическую, k=2 - среднюю квадратическую. При расчете различных степенных средних по одним и тем же данным статистического наблюдения средние не будут одинаковыми. Чем выше степень k средней, тем больше ее величина [8, c.104].

Структурные средние. Мода и медиана. Для характеристики величины варьирующего признака пользуются так называемыми структурными средними - модой и медианой.

Мода – это наиболее часто встречающееся значение ряда. Мода применяется, например, при определении размера одежды, обуви, пользующихся наибольшим спросом у покупателей, наиболее распространенной цены на тот или иной товар на рынке, и т.д.[8, c. 108].

В дискретном вариационном ряду наиболее часто встречающуюся варианту, имеющую наибольший вес. В интервальном вариационном ряду моду находят по следующей формуле:

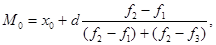                                                          (1.3.9)

где М₀ – мода;

х₀ – начало (нижняя граница) модального интервала (с наибольшей численностью);

d- величина модального интервала;

f₁ – частота интервала, предшествующего модальному;

f₂ -частота модального интервала;

f₃ – частота интервала, следующего за модальным.

Величина моды и медианы, как правило, отличается от величины средней, совпадая с ней только в случае симметрии вариационного ряда. Мода и медиана по-разному характеризуют совокупность. Мода определяет непосредственно размер признака, свойственный хотя и значительной части, но все же не всей совокупности. Мода по своему обобщающему значению менее точна по сравнению со средней арифметической, характеризующей совокупность в целом с учетом всех без исключения элементов совокупности.

Медианой является значение элемента, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения. Медиана делит ряд на две равные части. Она не зависит ни от амплитуды колебаний ряда, ни от распределения частот в пределах двух равных частей ряда, поэтому ее применение позволяет получить более точные результаты, чем при использовании других форм средних. Медиану определяют по формуле:

                                (1.3.10)

где М_е - медиана;

х₀ - нижняя граница медианного интервала;

d - величина медианного интервала;

åf – сумма частот ряда;

f_m  - частота медианного интервала;

S_m-1  - сумма накопленных частот интервалов, предшествующих медианному [8, c. 109].

Трудным вопросом методологии является вопрос о выборе вида средней. Здесь важно твердо усвоить, что решение этого вопроса зависит от характера исходного соотношения, выражающего данную среднюю величину, от содержания осредняемого признака, его связи с другими признаками, а также от особенностей исходного материала. Каждый из видов средних величин может выступать либо в форме простой, либо в форме взвешенной средней.

Толстик Н.В. в своем учебно-методическом пособии по статистике для студентов предлагает читателю «способ определения нужной формы средней, основанный на принципе выяснения сущности средней, ее социально-экономического содержания. Ведь средняя величина признака – это отношение. Поэтому прежде чем оперировать цифрами, необходимо выяснить, соотношением каких показателей, каких величин (в конечном счете) является средняя в данном случае. Это надо попробовать записать словами в виде формулы, которая будет логической формулой средней».

После того как словами записана логическая формула, которую надо вычислить, необходимо внимательно рассмотреть имеющиеся для вычисления данные и заменить словесные значения числителя и знаменателя логической формулы средней соответствующими числовыми значениями, после чего остается только рассчитать ответ. Этот принцип обеспечит правильный выбор формы средней, а значит, и правильное определение величины средней. Еще одно важное свойство принципа логической формулы средней заключается в том, что здесь не возникает проблемы выбора весов средней, которая часто порождает ошибки [8, c.110].