Теорема Менелая для треугольника.

Выпускная квалификационная работа

Избранные теоремы геометрии тетраэдра

 

Специальность / направление подготовки Математика

 

Специализация / профиль Математика - информатика

Содержание

 

Введение

Глава I. Виды тетраэдров и теоремы о тетраэдрах

1.1 Теоремы о тетраэдрах

§1. Теорема Менелая

§2. Теорема Чевы

§3. Свойства медиан и бимедиан тетраэдра

1.2 Различные виды тетраэдров.

§1. Пифагоровы тетраэдры

§2. Ортоцентрические тетраэдры

§3. Каркасные тетраэдры

§4. Равногранные тетраэдры

§5. Инцентрические тетраэдры

§6. Соразмерные тетраэдры

§7. Правильные тетраэдры

Глава II. Тетраэдр в курсе математики средней школы

§1. Сравнительная характеристика изложения темы «тетраэдр» в школьных учебниках

§2. Тестирование уровня развития пространственного мышления у учеников средней школы

Введение

 

Интерес к изучению тетраэдра возник у человечества с древних времен и не угасает до сих пор. Это связано не только с его красотой, но и с большой практической ценностью.

Тетраэдр является одним из основных фигур стереометрии, однако его изучение в курсе средней школы недостаточно подробно. В некоторых учебниках авторы избегают самой терминологии, предпочитая называть фигуру «треугольной пирамидой» (и рассматривают её именно в таком ключе), а об изучении различных видов тетраэдров зачастую и говорить не приходится.

Роль задач о тетраэдрах в математическом развитии школьников трудно переоценить. Они стимулируют накопление конкретных геометрических представлений, способствуют развитию пространственного мышления, что особенно важно в процессе изучения стереометрии.

Изучению тетраэдра как школе, так и в вузах посвящено лишь небольшое количество занятий, поэтому целью дипломной работы является изучение различных видов тетраэдров, а также теорем, связанных с геометрией тетраэдра. В соответствии с целью сформулированы следующие задачи:

1. Собрать сведения о тетраэдре из различных источников и привести их в систему; разобрать доказательства теорем, связанных с тетраэдром;

2. Проанализировать методику изложения материала в различных школьных учебниках;

3. Разработать курс занятий о тетраэдре для средней школы.

В первой главе моей дипломной работы речь пойдёт о различных видах тетраэдра и некоторых теоремах, касающихся этой фигуры. Вторая глава посвящена анализу учебного материала для средней школы по заданной теме и разработке курса занятий.

Глава I . Виды тетраэдров и теоремы о тетраэдрах

Теоремы о тетраэдрах

Теорема Менелая

Теорема Менелая для треугольника.

 

Пусть точки А₁ и С₁ лежат на сторонах В C и А C треугольника АВС, точка В₁ на продолжении стороны АС этого треугольника. Для того чтобы точки А₁, В₁, С₁ лежали на одной прямой необходимо и достаточно, чтобы выполнялось равенство = = =1.

Доказательство.

Сначала докажем необходимость. Пусть точки А₁,В₁,С₁ лежат на прямой l и     AA₀=h₁, CC₀=h₃ - перпендикуляры, опущенные соответственно из точек А, В, С на прямую l. Из подобия треугольников АА₀С₁ и ВВ₀С₁ получаем

. Аналогично, рассматривая другие пары подобных треугольников, получаем ; . Перемножая полученные пропорции, приходим к требуемому равенству.

 

Теперь докажем достаточность. Пусть точки А₁, В₁, С₁, лежащие на прямых ВС, АС, АВ таковы, что . Докажем, что точки А₁, В₁, С₁ лежат на одной прямой.

Проведем прямую А₁В₁ и докажем, что точка С₁ ей принадлежит. Предположим, что это не так. Сначала заметим, прямая А₁В₁ не параллельна прямой АВ. Пусть Т - точка пересечения А₁В₁ и АВ, тогда

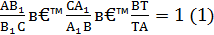. Из условия и равенства (1) следует, что . Так как точки Т и С₁ лежат вне отрезка АВ, их совпадение вытекает из следующей леммы.

Лемма 1.

Пусть А и В две различные точки, тогда для любого k>0, k≠1 на прямой АВ существуют две точки U и V такие, что 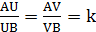, причем одна из этих точек принадлежит отрезку АВ, а другая лежит вне отрезка.

Доказательство.

 

 

Введем на прямой АВ координаты, приняв точку А за начало координат. Пусть для определенности k>1, тогда координата искомой точки U, лежащей внутри отрезка АВ, удовлетворяет уравнению , откуда 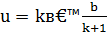. Точка V находится вне отрезка AB, из уравнения , откуда . Случай 0<k<1 отличается от рассмотренного лишь тем, что точку V следует искать левее точки А.

Теорема Менелая допускает интересное стереометрическое обобщение.