 |
Главная |
Ортоцентрические тетраэдры
|
из
5.00
|
В отличие от треугольника, высоты которого всегда пересекаются в одной точке - ортоцентре, не всякий тетраэдр обладает аналогичным свойством. Тетраэдр, высоты которого пересекаются в одной точке, называется ортоцентрическим. мы начнем изучение ортоцентрических тетраэдров с необходимых и достаточных условий ортоцентричности, каждое из которых можно принять за определение ортоцентрического тетраэдра.
(1) Высоты тетраэдра пересекаются в одной точке.
(2) Основания высот тетраэдра являются ортоцентрами граней.
(3) Каждые два противоположных ребра тетраэдра перпендикулярны.
(4) Суммы квадратов противоположных ребер тетраэдра равны.
(5) Отрезки, соединяющие середины противоположных ребер тетраэдра, равны.
(6) Произведения косинусов противоположных двугранных углов равны.
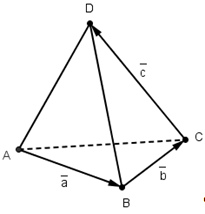
(7) Сумма квадратов площадей граней вчетверо меньше суммы квадратов произведений противоположных ребер.
Докажем некоторые из них.
Доказательство (3).
Пусть каждые два противоположных ребра тетраэдра перпендикулярны.
Следовательно, высоты тетраэдра попарно пересекаются. Если несколько прямых попарно пересекаются, то они лежат в одной плоскости или проходят через одну точку. В одной плоскости высоты тетраэдра лежать не могут, так как иначе в одной плоскости лежали бы и его вершины, поэтому они пересекаются в одной точке.
Вообще говоря, для того чтобы высоты тетраэдра пересекались в одной точке, необходимо и достаточно потребовать перпендикулярность только двух пар противоположных ребер. Доказательство этого предложения напрямую следует из следующей задачи.
Задача 1.
Дан произвольный тетраэдр ABCD. Докажите, что 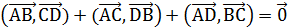 .
.
Решение.
Пусть а= 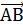 , b=
, b= 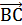 , с=
, с= 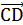 . Тогда
. Тогда 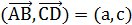 ,
, 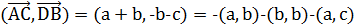 и
и 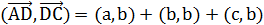 , складывая эти равенства, получаем требуемое.
, складывая эти равенства, получаем требуемое.
Далее докажем свойство (4).
Пусть а= 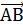 , b=
, b= 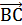 и с=
и с= 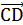 . Равенство
. Равенство 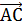 2+
2+ 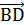 2=
2= 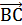 2+
2+ 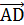 2, что
2, что 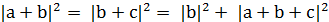 , т.е. (а,с)=0. Применяя данный алгоритм к другим парам противоположных ребер, очевидно, получим искомое утверждение.
, т.е. (а,с)=0. Применяя данный алгоритм к другим парам противоположных ребер, очевидно, получим искомое утверждение.
Приведем оказательство свойства (6).
Для доказательства используем следующие теоремы:
§ Теорема синусов. «Произведение длин двух противоположных ребер тетраэдра, деленное на произведение синусов двугранных углов при этих ребрах, одно и то же для всех трех пар противоположных ребер тетраэдра».
§ Теорема Бертшнейдера. «Если a и b – длины двух скрещивающихся ребер тетраэдра, а 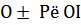 - двугранные углы при этих ребрах, то величина
- двугранные углы при этих ребрах, то величина 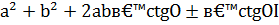 не зависит от выбора пары скрещивающихся ребер.
не зависит от выбора пары скрещивающихся ребер.
Воспользовавшись теоремой синусов для тетраэдра и теоремой Бертшнейдера, получаем, что произведения косинусов противоположных двугранных углов равны тогда и только тогда, когда равны суммы квадратов противоположных ребер, из чего и следует справедливость свойства (6) ортоцентрического тетраэдра.
В заключение пункта об ортоцентрическом тетраэдре решим несколько задач на эту тему.
Задача 2.
Докажите, что в ортоцентрическом тетраэдре выполняется соотношение ОН2=4R2-3d2, где О - центр описанной сферы, H - точка пересечения высот, R - радиус описанной сферы, d - расстояние между серединами противоположных ребер.
Решение.
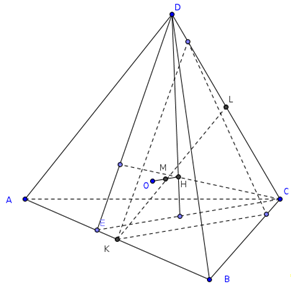
Пусть К и L - середины ребер АВ и СD соответственно. Точка Н лежитт в плоскости, проходящей через СD перепендикулярно АВ, а точка О - в плоскости, проходящей черех К перпендикулярно АВ.
Эти плоскости симметричны относительно центра масс тетраэдра - середины отрезка KL. Рассматривая такие плоскости для всех ребер, получаем, что точки Н и О симметричны относительно М, а значит КLМО - параллелограмм. Квадраты его сторон равны 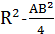 и
и 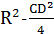 , поэтому
, поэтому 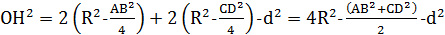 . Рассматривая сечение, проходящее через точку М параллельно АВ и СD, получаем что АВ2+CD2=4d2.
. Рассматривая сечение, проходящее через точку М параллельно АВ и СD, получаем что АВ2+CD2=4d2.
Здесь можно добавить, что прямую, на которой лежат точки О, М и Н, называют прямой Эйлера ортоцентрического тетраэдра.
Замечание.
Наряду с прямой Эйлера можно отметить существование сфер Эйлера для ортоцентрического тераэдра, о которых и пойдет речь в следующих задачах.
Задача 3.
Доказать, что для ортоцентрического тетраэдра окружности 9 точек каждой грани принадлежат одной сфере (сфере 24 точек). Для решения этой задачи необходимо доказать условие следующей задачи.
Задача 4.
Доказать, что середины сторон треугольника, основания высот и середины отрезков высот от вершин до точки их пересечения лежат на одной окружности - окружности 9 точек (Эйлер).
Доказательство.
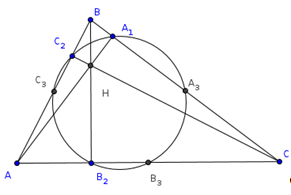
Пусть АВС - данный треугольник, Н - точка пересечения его высот, А1, В1, С1 - середины отрезков АН, ВН, СН; АА2 - высоты, А3 - середина ВС. Будем считать для удобства, что АВС - остроугольный треугольник. Поскольку 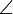 В1А1С1=
В1А1С1= 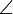 ВАС и ΔВ1А2С1=ΔВ1НС1, то
ВАС и ΔВ1А2С1=ΔВ1НС1, то 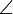 В1А2С1=
В1А2С1= 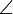 В1НС=180° -
В1НС=180° - 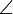 В1А1С1, т.е. точки А1, В1, А2, С1 лежат на одной окружности. Также легко увидеть, что
В1А1С1, т.е. точки А1, В1, А2, С1 лежат на одной окружности. Также легко увидеть, что 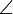 В1А3С1=
В1А3С1= 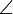 В1НС=180° -
В1НС=180° - 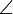 В1А1С1, т.е. точки А1, В1, А3, С1 тоже лежат на одной (а значит на той же) окружности. Отсюда следует, что все 9 точек, о которых говорится в условии, лежат на одной окружности. Случай тупоугольного треугольника АВС рассматривается аналогично.
В1А1С1, т.е. точки А1, В1, А3, С1 тоже лежат на одной (а значит на той же) окружности. Отсюда следует, что все 9 точек, о которых говорится в условии, лежат на одной окружности. Случай тупоугольного треугольника АВС рассматривается аналогично.
Заметим, что окружность 9 точек гомотетична описанной окружности с центром в Н и коэффициентом  (именно так расположены треугольники АВС и А1В1С1). С другой стороны, окружность 9 точек гомотетична описанной окружности с центром в точке пересечения медиан треугольника АВС и коэффициентом
(именно так расположены треугольники АВС и А1В1С1). С другой стороны, окружность 9 точек гомотетична описанной окружности с центром в точке пересечения медиан треугольника АВС и коэффициентом 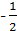 (именно так расположены треугольники АВС и треугольник с вершинами в серединах его сторон).
(именно так расположены треугольники АВС и треугольник с вершинами в серединах его сторон).
Теперь, после определения окружности 9 точек, можно перейти к доказательству условия задачи 3.
Доказательство.
Сечение ортоцентрического тетраэдра любой плоскостью, параллельной противоположным ребрам и проходящей на равном расстоянии от этих ребер, есть прямоугольник, диагонали которого равны расстоянию между серединами противоположных ребер тетраэдра ( все эти расстояния равны между собой, см. необходимое и достаточное условие ортоцентричности (5). Отсюда следует, что середины всех ребер ортоцентрического тетраэдра лежат на поверхности сферы, центр которой совпадает с центром тяжести данного тетраэдра, а диаметр равен расстоянию между серединами противоположных ребер тетраэдра. Значит, все четыре окружности 9 точек лежат на поверхности этой сферы.
Задача 5.
Доказать, что для ортоцентрического тетраэдра центры тяжести и точки пересечения высот граней, а также точки , делящие отрезки каждой высоты тетраэдра от вершины до точки пересечения высот в отношении 2:1, лежат на одной сфере ( сфере 12 точек).
Доказательство.
Пусть точки О, М и Н - соответственно центр описанного шара, ценетр тяжести и ортоцентр ортоцентрического тетраэдра; М - середина отрезка ОН (см. задачу 2). Центры тяжести граней тетраэдра служат вершинами тетраэдра, гомотетичного, с центром гомотетиии в точке М и коэффициентом 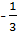 , при этой гомотетии точка О перейдет в точку О1, расположенную на отрезке МН так, что
, при этой гомотетии точка О перейдет в точку О1, расположенную на отрезке МН так, что 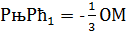 , О1 будет центром сферы проходящей через центры тяжестей граней.
, О1 будет центром сферы проходящей через центры тяжестей граней.
С другой стороны, точки, делящие отрезки высот тетраэдра от вершин до ортоцентра в отношении 2:1, служат вершинами тетраэдра, гомотетичного данному с центром гомотетии в Н и коэффициентом  . При этой гомотетии точка О, как легко видеть, перейдет в ту же точку О1. Таким образом, восемь из двенадцати точек лежат на поверхности сферы с центром в О1 и радиусом, втрое меньшим, чем радиус сферы, описанной около тетраэдра.
. При этой гомотетии точка О, как легко видеть, перейдет в ту же точку О1. Таким образом, восемь из двенадцати точек лежат на поверхности сферы с центром в О1 и радиусом, втрое меньшим, чем радиус сферы, описанной около тетраэдра.
Докажем, что точки пересечения высот каждой грани лежат на поверхности той же сферы.
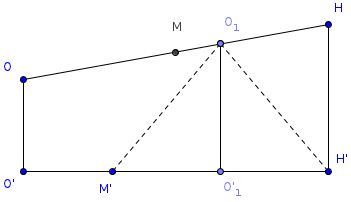
Пусть О`, Н` и М` - центр описанной окружности, точка пересечения высот и центр тяжести какой-либо грани. О` и Н` являются проекциями точек О и Н на плоскость этой грани, а отрезок М` делит отрезок О`Н` в отношении 1:2, считая от О`(известный планиметрический факт). Теперь легко убедиться (см. рис), что проекция О1 на плоскость этой грани - точка О`1 совпадает с серединой отрезка М`Н`, т.е. О1 равноудалена от М` и Н`, что и требовалось.
Каркасные тетраэдры
Каркасным называется тетраэдр, для которого существует сфера, касающаяся всех шести ребер тетраэдра. Не всякий тетраэдр каркасный. Например, легко понять, что нельзя построить сферу, касающуюся всех ребер равногранного тетраэдра, если его описанный параллелепипед "длинный".
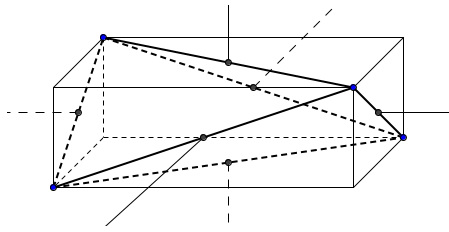
Перечислим свойства каркасного тетраэдра.
(1) Существует сфера, касающаяся всех ребер тетраэдра.
(2) Суммы длин скрещивающихся ребер равны.
(3) Суммы двугранных углов при противоположных ребрах равны.
(4) Окружности, вписанные в грани, попарно касаются.
(5) Все четырехугольники, получающиеся на развертке тетраэдра, — описанные.
(6) Перпендикуляры, восстановленные к граням из центров вписанных в них окружностей, пересекаются в одной точке.
Докажем несколько свойств каркасного тераэдра.
Доказательство (2).
Пусть О - центр сферы, касающейся четырех ребер во внутренних точках. заметим теперь, что если из точки Х провести касательные ХР и ХQ к сфере с центром О, то точки Р и Q симметричны относительно плоскости, проходящей прямую ХО и середину отрезка PQ, а значит плоскости РОХ и QОХ образуют с плоскостью ХРQ равные углы.
Проведем 4 плоскости, проходящие через точку О и рассматриваемые ребра тетраэдра. Они разбивают каждый из рассматриваемых двугранных углов на два двугранных угла. Выше было показано, что полученные двугранные углы, прилегающие к одной грани тетраэдра, равны. Как в одну, так и в другую рассматриваемую сумму двугранных углов входит по одному полученному углу для каждой грани тетраэдра. Проводя аналогичные рассуждения для других пар скрещивающихся ребер, получим справедливость свойства (2).
Вспомним некоторые свойства описанного четырехугольника:
a) Плоский четырехугольник будет описанным тогда и только тогда, когда суммы его противоположных сторон равны;
b) Если описанный четырехугольник разбить диагональю на два треугольника, то вписанные в треугольники окружности касаются
Учитывая эти свойства, легко доказать остальные свойства каркасного тетраэдра. Свойство (3) тетраэдра напрямую следует из свойства (b), а свойство (4) из свойства (a) и свойства (1) тетраэдра. Свойство (5) из свойства (3). Действительно, ведь окружности вписанные в грани тетраэдра, являются пересечениями его граней со сферой, касающейся ребер, откуда очевидно, что перпендикуляры, восстановленные в центрах вписанных в грани окружностей неминуемо пересекутся в центре этой сферы.
Задача 1.
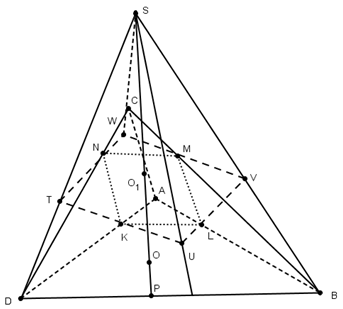
Сфера касается ребер АВ, ВС, СD и DA тетраэдра АВСD в точках L, M, N, K, являющихся вершинами квадрата. Докажите, что если эта сфера касается ребра АС, то она касается и ребра BD.
Решение.
По условия КLMN - квадрат. Проведем через точки К, L, M, N плоскости, касающиеся сферы. Т.к все эти плоскости одинаково наклонены к плоскости КLMN, то они пересекаются в одной точке S, расположенной на прямой ОО1, где - центр сферы, а О1 - центр квадрата. Эти плоскости пересекают поверхность квадрата KLMN по квадрату TUVW, серединами сторон которого являются точки К, L, M, N. В четырехгранном угле STUVW с вершиной S все плоские углы равны, а точки К, L, M, N лежат на биссектрисах его плоских углов, причем SK=SL=SM=SN. Следовательно,
SA=SC и SD=SB, а значит АК=АL=CM=CN и ВL=BM=DN=DK. По условию АС тоже касается шара, поэтому А C =АК+CN=2АК. А так как SK - биссектриса угла DSA, то DK:КА=DS:SA=DВ:АС. Из равенства АС=2АК следует теперь, что DВ=2DK. Пусть Р - середина отрезка DВ, тогда Р лежит на прямой SO. Треугольники DOK и DOP равны, т.к. DK=DP и 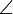 DКO=
DКO= 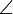 DPO=90°. Поэтому ОР=ОК=R, где R - радиус сферы, а значит, DB тоже касается сферы.
DPO=90°. Поэтому ОР=ОК=R, где R - радиус сферы, а значит, DB тоже касается сферы.
|
из
5.00
|
Обсуждение в статье: Ортоцентрические тетраэдры |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

