Теорема Менелая для тетраэдра.

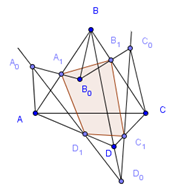
Если плоскость μ пересекает ребра АВ, ВС, CD и DA тетраэдра АВСD в точках А₁, В₁, С₁, D₁, то  (2).

Обратно, если для четырех точек А₁, В₁, С₁, D₁,лежащих соответственно на ребрах АВ, ВС, СD, DA тетраэдра, выполнено равенство (2), то эти четыре точки лежат в одной плоскости.

Доказательство.

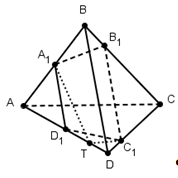
Пусть h₁, h₂, h_3, h₄ - расстояния от точек А, В, С, D соответственно до плоскости μ, тогда ; ; ; .

Осталось перемножить полученные отношения.

Для доказательства обратной теоремы построим плоскость А₁, В₁, С₁. Пусть эта плоскость пересекает ребро DA в точке Т.

По доказанному , а по условию , поэтому (и по лемме) точки Т и D₁ совпадают. Утверждение доказано.

Теорема Чевы

Теорема Чевы для треугольника.

Пусть точки А₁, В₁,С₁ лежат соответственно на сторонах ВС, АС и ВА треугольника АВС (см. рис). Для того чтобы отрезки АА₁, ВВ₁, СС₁ пересекались в одной точке, необходимо и достаточно, чтобы выполнялось соотношение:  (3) (отрезки АА₁, ВВ₁, СС₁ иногда называют чевианами).

Доказательство.

Необходимость. Пусть отрезки АА₁, ВВ₁, СС₁ пересекаются в точке М внутри треугольника АВС.

Обозначим через S₁, S₂, S₃ площади треугольников АМС, СМВ, АМВ, а через h₁, h₂ - расстояния от точек А и В до прямой МС. Тогда  аналогично , . Перемножив полученные пропорции, убеждаемся в справедливости теоремы.

Достаточность. Пусть точки А₁, В₁, С₁ лежат на сторонах ВС, СА, АС треугольника, и выполнено соотношение (3), М - точка пересечения отрезков АА₁и ВВ₁, а отрезок СМ пересекает сторону АВ в точке Q. Тогда, по уже доказанному , . Из леммы снова следует совпадение точек Q=C₁. Достаточность доказана.

Перейдем теперь к пространственному обобщению теоремы Чевы.

Теорема Чевы для тетраэдра.

Пусть М - точка внутри тетраэдра АВСD, а А₁, В₁, С₁ и D₁ - точки пересечения плоскостей СМD, AMD, АМВ и СМВ с ребрами АВ, В C , СD и DA соответственно. Тогда  (4). Обратно: если для точек , то плоскости АВС, ВСD₁ и DAB₁ проходят через одну точку.

Доказательство.

Необходимость легко получить, если заметить, что точки А₁, В₁, С₁, D₁ лежат в одной плоскости (эта плоскость проходит через прямые А₁С₁ и В₁D₁, пересекающиеся в точке М), и применить теорему Менелая. Обратная теорема доказывается так же, так и обратная теореме Менелая в пространстве: нужно провести плоскость через точки А₁, В₁, С₁ и доказать с помощью леммы, что эта плоскость пересечет ребро DA в точке D₁.

Свойства медиан и бимедиан тетраэдра

Медианой тетраэдра называется отрезок, соединяющий вершину тетраэдра с центром тяжести противоположной грани (точкой пересечения медиан).

Теорема (Применение теоремы Менелая).

Медианы тетраэдра пересекаются в одной точке. Эта точка делит каждую медиану в отношении 3:1, считая от вершины.

Доказательство.

Проведем две медианы: DD ₁ и CC ₁ тетраэдра ABCD. Эти медианы пересекутся в точке F. CL – медиана грани ABC , DL – медиана грани ABD, а D ₁ , C ₁ – центры тяжести грани ABC и ABD. По теореме Менелая: 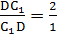 и . Запишем теорему для треугольника DLD ₁: ;  =>  Доказательство производится аналогично для любой другой пары медиан.