 |
Главная |
Изложение темы «Тетраэдр» в учебнике «Геометрия» для 7-11 классов Погорелова А.В.
|
из
5.00
|
В другом базовом учебнике А.В. Погорелова и др.теоретический материал в той или иной степени касающийся темы «Тетраэдр» содержится в пунктах 176-180, 186, 192, 199, 200.
В пункте 180 “Правильные многогранники” содержится определение понятия «правильный тетраэдр» (“Тетраэдр представляет собой треугольную пирамиду, у которой все рёбра равны”), доказательство некоторых свойств и теорем о пирамиде проиллюстрировано чертежами тетраэдра. Однако в данном учебном пособии акцент на изучении фигуры не ставится, и в этом смысле его информативность (касательно тетраэдра) можно оценить как низкую. Практический же материал учебника содержит удовлетворительное количество заданий, касающихся пирамиды, в основании которой расположен треугольник (что по сути и есть тетраэдр). Приведём примеры решения некоторых задач.
Решение задач.
Задача 1 (№ 41 из пункта «Многогранники»).
Основание пирамиды — равнобедренный треугольник, у которого основание равно 12 см, а боковая сторона — 10 см. Боковые грани образуют с основанием равные двугранные углы, содержащие по 45°. Найдите высоту пирамиды.
Решение:
Проведем перпендикуляр SO к плоскости основания и перпендикуляры SK, SM и SN к сторонам ΔABС. Тогда по теореме о трех перпендикулярах OK  BC, ОМ
BC, ОМ  АС и ON
АС и ON  AB.
AB.
Тогда, 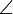 SKO =
SKO = 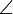 SMO =
SMO = 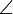 SNO = 45° — как линейные углы данных двугранных углов. А следовательно, прямоугольные треугольники SKO, SMO иSNO равны по катету и острому углу. Так что OK=OM=ON, то есть точка О является центром окружности, вписаннойв ΔАВС.
SNO = 45° — как линейные углы данных двугранных углов. А следовательно, прямоугольные треугольники SKO, SMO иSNO равны по катету и острому углу. Так что OK=OM=ON, то есть точка О является центром окружности, вписаннойв ΔАВС.
Выразим площадь прямоугольника АВС:
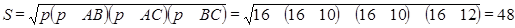 (см)
(см)
С другой стороны, 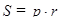 . Так что
. Так что 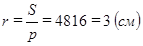 ; ОК=r=3 см. Так как в прямоугольном треугольнике SOK острый угол равен45°, то ΔSOK является равнобедренным и SO=OK=3(см).
; ОК=r=3 см. Так как в прямоугольном треугольнике SOK острый угол равен45°, то ΔSOK является равнобедренным и SO=OK=3(см).
Задача 2 (№ 43 из пункта «Объёмы многогранников»).
Найдите объем пирамиды, имеющий основанием треугольник, два угла которого a и β; радиус описанного круга R. Боковые ребра пирамиды наклонены к плоскости ее основания под углом γ.
Решение.
Так как все боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, то высота пирамиды O1O проходит через центр описанной около основания окружности. Так что 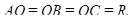
Далее, в прямоугольном  :
: 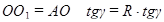 .
.
В ΔАВС 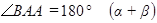 . Тогда согласно теореме синусов
. Тогда согласно теореме синусов
 .
.
Так что 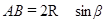 ,
, 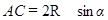 ,
, 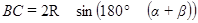 =
=
=  .
.
Площадь треугольника 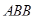 :
:
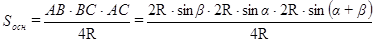 .
.
Тогда 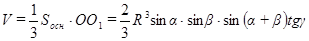 .
.
Изложение темы «Тетраэдр» в учебнике «Геометрия» для 10-11 классов Александрова А.Д.
Рассмотрим учебное пособие Александрова А.Д. и др. «Геометрия: учебник для учащихся 11 кл. с углубленным изучением математики». Отдельных параграфов, посвящённых тетраэдру в этом учебнике нет, однако тема присутствует в виде фрагментов других параграфов.
Впервые тетраэдр упоминается в §21.3. В материале параграфа рассматривается теорема о триангуляции многогранника, в качестве примера выполняют триангуляцию выпуклой пирамиды. Само понятие «многогранник» в учебнике трактуется двумя способами, второе определение понятия напрямую связано с тетраэдром: «Многогранник – это фигура, являющаяся объединением конечного числа тетраэдров…». Познания, касающиеся правильной пирамиды и некоторых аспектов симметрии тетраэдра можно обнаружить в §23.
В §26.2 описано применение теоремы Эйлера («о правильных сетях») для правильных многогранников (в т.ч. для тетраэдра), а в §26.4 рассматриваются виды симметрий, характерные для этих фигур.
Формулу для нахождения объёма пирамиды авторы вводят в задаче №30.1(2), а площадь боковой поверхности пирамиды вводится в материале параграфа «Площадь поверхности конуса и цилиндра» (§32.5).
Также, в учебнике можно найти информацию о средней линии тетраэдра, центре масс (§35.5) и классе равногранных тетраэдров. Движения I и II рода демонстрируются в ходе решения задач о тетраэдрах.
Отличительная особенность учебника — высокая научность, которую авторам удалось совместить с доступным языком и чёткой структурой изложения. Приведём примеры решения некоторых задач.
Решение задач.
Задача 1.
В данную правильную треугольную усечённую пирамиду с боковым ребром a можно поместить сферу, касающуюся всех граней, и сферу, касающуюся всех рёбер. Найдите стороны оснований пирамиды.
Решение.
Изобразим на чертеже «полную» пирамиду. Данная пирамида  ,
,  — высота «полной» пирамиды,
— высота «полной» пирамиды, 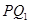 — ее часть до верхнего основания усеченной. Задача сводится к планиметрической, при этом не надо рисовать ни одной из данных сфер. Т.к. в усеченную пирамиду можно вписать сферу, касающуюся всех ребер, то в её боковую грань можно вписать окружность. Обозначим
— ее часть до верхнего основания усеченной. Задача сводится к планиметрической, при этом не надо рисовать ни одной из данных сфер. Т.к. в усеченную пирамиду можно вписать сферу, касающуюся всех ребер, то в её боковую грань можно вписать окружность. Обозначим 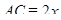 ,
, 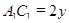 (для удобства деления пополам) и для описанного четырехугольника
(для удобства деления пополам) и для описанного четырехугольника  получим, что
получим, что 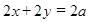 , откуда
, откуда
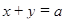 . (1)
. (1)
Из существования вписанного шара следует, что существует полуокружность, расположенная в трапеции 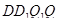 (
( 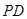 — апофема «полной» пирамиды) так, что ее центр лежит в середине
— апофема «полной» пирамиды) так, что ее центр лежит в середине 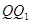 , а сама она касается остальных трёх сторон трапеции.
, а сама она касается остальных трёх сторон трапеции.
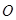 — центр шара,
— центр шара,  и
и  — точки касания. Тогда
— точки касания. Тогда 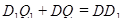 . Выразим эти величину через
. Выразим эти величину через 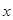 и
и 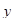 . Из
. Из 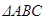 :
:  . Из
. Из 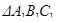 :
: 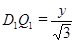 . Из трапеции
. Из трапеции 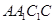 :
: 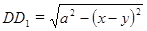 . Получаем уравнение:
. Получаем уравнение:
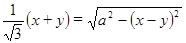 .(2)
.(2)
Решив систему уравнений (1) и (2), получим, что стороны оснований равны  .
.
Задача 2.
Внутри правильного тетраэдра с ребром a расположены четыре равные сферы так, что каждая сфера касается трех других сфер и трех граней тетраэдра. Найти радиус этих сфер.
Решение.
 — данный тетраэдр,
— данный тетраэдр, 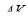 — его высота,
— его высота, 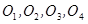 — центры сфер,
— центры сфер,  — точка пересечения прямой
— точка пересечения прямой 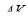 с плоскостью
с плоскостью  . Заметим, что центры равных сфер
. Заметим, что центры равных сфер 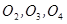 , касающихся плоскости
, касающихся плоскости 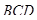 , удалены от нее на равные расстояния, каждое из которых равно радиусу шара (обозначием его как x). Значит плоскости
, удалены от нее на равные расстояния, каждое из которых равно радиусу шара (обозначием его как x). Значит плоскости  и
и 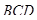 параллельны, а потому
параллельны, а потому  .
.
Далее, каждая пара шаров касается между собой, а потому расстояние между центрами равно сумме их радиусов, то есть 2x . Имеем:
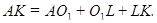 . Но
. Но 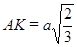 как высота правильного тетраэдра с ребром
как высота правильного тетраэдра с ребром 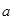 ;
; 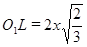 как высота правильного тетраэдра с ребром 2x;
как высота правильного тетраэдра с ребром 2x; 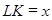 .
.
Осталось выразить 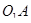 . Заметим, что точка
. Заметим, что точка  находится внутри трехгранного угла и удалена от его граней на расстояние
находится внутри трехгранного угла и удалена от его граней на расстояние 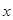 , а плоские углы трехгранного угла равны
, а плоские углы трехгранного угла равны 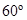 . Не сложно получить то, что
. Не сложно получить то, что 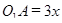 . Приходим к уравнению:
. Приходим к уравнению:
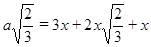 , откуда после упрощений получаем
, откуда после упрощений получаем 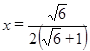 .
.
|
из
5.00
|
Обсуждение в статье: Изложение темы «Тетраэдр» в учебнике «Геометрия» для 7-11 классов Погорелова А.В. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

