Отношение длины здания Парфенона в Афинах к его высоте равно Ф.

Пифагор – древнегреческий философ-идеалист, математик, основатель пифагореизма, политический, религиозный деятель. Его родиной был остров Самос (отсюда и прозвище - Самосский), где он появился на свет приблизительно в 580 г. до н. э. Его отцом был резчик по драгоценным камням. Образование у Пифагора было очень хорошим, юношу обучало много наставников, следующим местом, где Пифагор совершенствовал познания, стал Милет, там его ждало знакомство с Фалесом , ученым, посоветовавшим ему поехать в Египет. Среди наук, которых он хорошо освоил в Египте, была и математика. Следующие 12 лет он прожил в Вавилоне, где также с ним делились своими познаниями жрецы. Согласно легендам, Пифагор побывал и в Индии.

В Кротоне Пифагор выступил организатором собственной школы, которая была одновременно и политической структурой, и религиозно-монашеским орденом со своим уставом и очень строгими правилами. В частности, все члены пифагорейского союза не должны были употреблять мясную пищу, раскрывать другим учение своего наставника, отказывались иметь личную собственность.

Поскольку Пифагор считал свое учение тайной и практиковал только устную передачу его ученикам, собрания сочинений после него не осталось. Некоторые сведения все-таки стали явными, однако разграничить истину и выдумки невероятно сложно.

Согласно Порфирию и сам Пифагор погиб в результате антипифагорейского мятежа в Метапонте, однако другие авторы не подтверждают этой версии, хотя охотно передают историю о том, будто бы удручённый философ уморил себя голодом в священном храме.

                               Всё есть число.

               Все упорядочивается согласно чисел.

                         Числа правят миром.

v Пифагор признавал только целое положительное число (натуральное), разделяя их на четные и нечетные

v Была доказана теорема делимости (произведение двух чисел четно, когда четно хотя бы одно из них)

v Ввел понятие «совершенного числа» (число, которое равно сумме своих делителей)

         6 = 1+2+3       28 = 1 + 2 + 4 + 7 +14

496 =1+2+4+8+16+31+62+124+248      

8128 =                 

v Ввел понятие простого числа (делится само на себя и на1)

v Решил квадратные уравнения геометрическим способом

Возьмем отрезок, длиной х и отрезок, длиной 5  (10:2) и построим квадрат со стороной Х+5

Площадь квадрата равна

Из уравнения видно, что , следовательно заштрихованная часть квадрата равна 39, а вся площадь равна 39 + 25 = 64

Следовательно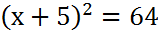   

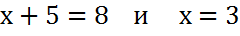
(отрицательных чисел при Пифагоре еще не знали)

Так же можно доказать формулу квадрата суммы

 

 

v Доказал теорему Пифагора

 

 

V век до нашей эры

Пифагорейская школа

v Появляется необходимость в иррациональных числах.

      Три задачи древности, которые нельзя построить с помощью циркуля и линейки.

Соизмеримыми называются отрезки, если отношение их длин является рациональным числом

1) Задача о несоизмеримости стороны квадрата и его диагонали.

Если сторона квадрата равна  , то его диагональ равна  

                         

2). Задача об удвоении куба. Построить куб с объемом в 2 раза больше данного.  

Если сторона куба равна 1, то его объем равен 1. Объем нового куба равен 2, тогда его сторона равна  .

  

                          

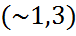
3).Задача о квадратуре круга. Построить квадрат, равновеликий данному кругу.

Если радиус круга равен 1, то его площадь равна 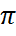. Если площадь квадрата равна 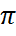, то его сторона равна .

                   

                    

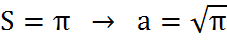
v Земля имеет форму шара и находится в центре

Вселенной

v    «Золотое сечение»

“Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора, а другое - деление отрезка в среднем и крайнем отношении … Первое можно сравнить с мерой золота ; второе же больше напоминает драгоценный камень.”

Иоганн Кеплер

 

1. Символом Пифагорейской школы была пентаграмма – пятиконечная звезда, она же считалась амулетом здоровья. Эта удивительная фигура, в которой наблюдается постоянство отношений отрезков.

 

 

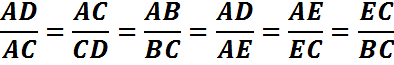
Рассмотрим отрезок AD и точку С, которая делит отрезок на две части, причем весь отрезок относится к большей части, как большая часть – к меньшей.

                                             a

A             b              C       a-b  D

               поделим на

         

 обозначим  за Ф – число Фидия

                 

                  618…

 

(Ф = 1 + )         

    2).

3).    -  обладают аддитивным свойством, т.е. каждый последующий член равен сумме двух предыдущих.   

 ( , сократим на  и получим )

   

 

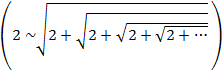
  Фидий – древнегреческий инженер, руководил постройкой Парфенона в Афинах в V веке до н.э. и при строительстве неоднократно применял это соотношение. Соразмерность, выраженная числом Ф наиболее приятна для глаза. Леонардо де Винчи назвал деление отрезка в отношении Ф «золотым сечением»

2. «Золотой прямоугольник» - у которого длина относится к ширине, как Ф. Если от него отрезать квадрат, то получится опять «золотой прямоугольник»

Прямоугольники ABCD,  ABKM , EBKF – «золотые»

                 Парфенон в Греции

Отношение длины здания Парфенона в Афинах к его высоте равно Ф.

КВ : АВ = СВ :АС= АВ : ВС = Ф.

 

3. «Золотой треугольник» - это равнобедренный треугольник, у которого боковая сторона относится к основанию, как Ф. Длины биссектрис углов при основании равны самому основанию.

 = 1,618…. 

Треугольники ABC, ANC, AMC – «золотые»

Углы 1, 2, 3, 4 и 5 равны по 36

AC = MC = NA

                        

 «Портрет Моны Лизы» («Джоконда»)  Леонардо да Винчи построен на "золотых треугольниках". Зрачок левого глаза, через который проходит вертикальная ось полотна, находится на пересечении двух биссектрис верхнего золотого треугольника,

 

3.  «Золотой кубоид» - это прямоугольный параллелепипед с ребрами Ф, 1 и . Площадь поверхности его равна 4Ф, а диагональ равна 2.