Теория Гинзбурга – Ландау

 

В 1950 году В. Л. Гинзбург и Л. Д. Ландау построили теорию сверхпроводимости, основанную на квантовой механике. Их теория является феноменологической, поскольку в ней принимаются определенные предположения, доказательством справедливости которых является то, что они правильно описывают некоторые свойства сверхпроводников.

В теории Гинзбурга — Ландау предполагается, что вся совокупность сверхпроводящих электронов описывается волновой функцией Ш(r) от одной пространственной координаты. Вообще говоря, волновая функция п электронов втвердом теле есть функция п координат .

Введением функции Ш(r) устанавливалось когерентное согласованное поведение всех сверхпроводящих электронов. Действительно, если все n_s электронов ведут себя совершенно одинаково, согласованно, то для описания их поведения достаточно той же самой волновой функции, что и для описания поведения одного электрона, т. е. функции от одной переменной. Величину |Ш(r)|² можно рассматривать как плотность сверхпроводящих электронов, которая обращается в нуль при Т=Т_С.

Теория Гинзбурга — Ландау исходит далее из того, что переход из нормального состояния в сверхпроводящее в отсутствие внешнего поля является фазовым переходом II рода. Теория таких переходов была разработана Ландау несколько раньше. В этой теории присутствовал некоторый параметр порядка, который в новой фазе (в нашем случае — в сверхпроводящей фазе) должен монотонно возрастать от нуля при Т=Т_С до единицы при Т=0 К. В качестве этого параметра Гинзбург и Ландау выбрали функцию Ш(r) .

Далее задача сводится к нахождению функции Ш(r) и векторного потенциала поля А(r), которые соответствуют минимуму свободной энергии сверхпроводящей фазы при определенных граничных условиях. В результате минимизации свободной энергии по Ш и по А были получены уравнения, получившие название уравнений Гинзбурга — Ландау. Рассмотрим, как это можно сделать.

Итак, Ш(r) – параметр порядка. Нормировка этой волновой функции выбирается так, чтобы |Ш(r)|²=n_s/2, т.е. так, чтобы квадрат ее модуля равнялся половине плотности сверхпроводящих электронов. Рассмотрим однородный сверхпроводник без внешнего поля. Разложим свободную энергию Геймгольца по степеням |Ш|² вблизи Т_С:

 

 

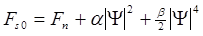
где F_s0 – свободная энергия Геймгольца в свепрхпроводящем состоянии в отсутствие поля, а F_n - свободная энергия Геймгольца в нормальном состоянии. б и в - коэффициенты разложения. Найдем то значение | Ш |² , при котором свободная энергия однородного сверхпроводника F_{s 0} достигает минимум. Это значение |Ш|² будет решением уравнения

 

 

Найдем соответствующую производную.

 

 

отсюда найдем |Ш|²

 

| Ш |² =-б/в

 

Подставим:

F_s0= F_n -б²/в + б²/2в= F_n - б²/2в (29)

 

Энергия сверхпроводящего состояния должна быть меньше энергии нормального, а для этого в>0 при Т<Т_С. Ясно, что |Ш|²>0 поэтому б<0. При Т>Т_с F_s0>F_n, поэтому в>0 и б>0. Таким образом, в>0 и не зависит от температуры. Тогда в первом приближении мы можем считать в=const. Поскольку при Т=Т_с параметр порядка должен быть равен нулю, а при Т<Т_с — отличен от нуля, следовательно, б=0 при Т=Т_С и б<0 при Т<Т_с. Поэтому в первом порядке по (Т_с-Т) можно записать

 

б~(Т-Т_с)=б₀(Т-Т_с)

 

Из формулы (30) получим

 

F_n-F_s0=б²/2в

 

Но эта разность равна H²_cm/8р откуда имеем

 

H²_cm = 4рб²/в

 

Теперь рассмотрим сверхпроводник в магнитном поле. Для такого сверхпроводника плотность свободной энергии Гиббса будет иметь вид

 

 

Т.е. в нашем случае

 

где G_n - плотность свободной энергии сверхпроводника и нормальном состоянии, Н₀ — напряженность внешнего однородного магнитного поля, в котором находится сверхпроводник. Предпоследнее слагаемое представляет собой плотность магнитной энергии. Слагаемое с градиентным членом — это плотность кинетической энергии сверхпроводящих электронов. Полная энергия Гиббса сверхпроводника в магнитном поле будет равна

 

 

В равновесном состоянии эта энергия должна иметь минимум. . Для решения этой вариационной задачи будем считать Ш(r) и А(r) неизменными, а поварьируем функцию Ш*(r) . Итак, решаем вариационную задачу

 

 

Вынести дШ* за квадратные скобки мешает только . Проделаем такие преобразования. Обозначим

 

 

Используя тождество

 

 

имеем

 

Последний интеграл в этом равенстве по теореме Гаусса, превращается в поверхностный интеграл:

 

 

подставляя полученные соотношения, получим

 

 

Это выражение может быть равно нулю при произвольной дШ* только в том случае, если выражения в квадратных скобках равны нулю. Так мы получим первое уравнение теории ГЛ и граничное условие к нему:

 

 

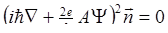
Варьирование по Ш(r) даст комплексно сопряженное выражение. Новый результат можно получить варьированием А(r).

 

 

Т.к. поле на поверхности задано (Н₀=const), то rot Н₀=0, а также равен нулю поверхностный интеграл.

Из векторного анализа известно, что div[ab] = brota - arotb , или применительно к нашему случаю .

С учетом, того что 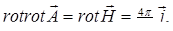, получим соотношение

 

 

Эти уравнения можно записать в более компактной форме, если перейти к безразмерной волной функции

 

ш(r)= Ш(r)/ Ш₀

 

где Ш₀²=n_s/2=|б|/в и введем обозначения

 

 

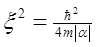
Тогда уравнения Гинзбурга – Ландау примут вид

 

 

где Ф₀=рħс/ e — квант потока.