 |
Главная |
РАСЧЕТ И ПОСТРОЕНИЕ СТРУКТУРНЫХ ХАРАКТЕРИСТИК ВАРИАЦИОННОГО РЯ
|
из
5.00
|
ОПРЕДЕЛЕНИЕ МОДЫ
Мода – значение признака, чаще всего встречающееся в совокупности. Для дискретного вариационного ряда мода определяется по частотам вариант и соответствует варианте с максимальной частотой. В интервальном вариационном ряду с равными интервалами модальный интервал определяется по наибольшей частоте.
Мода определяется по следующей формуле:
 (6.1)
(6.1)
где Мо – мода;
 - нижняя граница модального интервала;
- нижняя граница модального интервала;
 - величина модального интервала;
- величина модального интервала;
 - частота модального интервала;
- частота модального интервала;
 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;
 - частота интервала, последующего за модальным.
- частота интервала, последующего за модальным.
Для таблицы 3.2 рассчитаем моду. В данном распределении интервал 121-1814 будет модальным, так как он имеет наибольшую частоту. Определим моду:

Моду в интервальном ряду можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который является в данном случае модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс.
Абсцисса точки пересечения этих прямых и будет модой распределения. На рисунке 6.1 представлено графическое изображение моды для ряда распределения, представленного в таблице 3.2.

Рис. 6.1 Графическое определение моды по гистограмме
Для ряда распределения, представленного в таблице 3.4, определим моду. В данном распределении интервал 2,17-19,52 будет модальным, так как он имеет наибольшую частоту. Мода:

Графическое построение моды для данной совокупности представлено на рис. 6.2.
Для ряда распределения, представленного в таблице 3.6, определим моду. В данном распределении интервал15800-5460 будет модальным, так как он имеет наибольшую частоту. Мода:
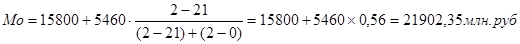
Графическое построение моды для данной совокупности представлено на рис. 6.3.

Рис. 6.2. Графическое определение моды по гистограмме
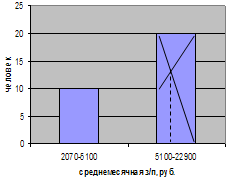
Рис. 6.3. Графическое определение моды по гистограмме
РАСЧЕТ МЕДИАНЫ
Медиана – значение изучаемого признака, приходящееся на середину ранжированной совокупности. При вычислении медианы интервального вариационного ряда сначала находят медианный интервал  , где h – длина медианного интервала. Для этого можно использовать кумулятивное распределение частот или относительных частот. Медианному интервалу соответствует тот, в котором содержится накопленная частота, равная ½. Внутри найденного интервала расчет медианы производится по формуле:
, где h – длина медианного интервала. Для этого можно использовать кумулятивное распределение частот или относительных частот. Медианному интервалу соответствует тот, в котором содержится накопленная частота, равная ½. Внутри найденного интервала расчет медианы производится по формуле:
 , (6.2)
, (6.2)
где  - медиана;
- медиана;
 - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
 - величина медианного интервала;
- величина медианного интервала;
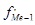 - накопленная частота интервала, предшествующего медианному;
- накопленная частота интервала, предшествующего медианному;
 - частота медианного интервала;
- частота медианного интервала;
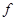 - накопленная частота.
- накопленная частота.
Медиану в интервальном ряду можно определить графически. Медиана рассчитывается по кумуляте. Для ее определения из точки на шкале накопленных частот, соответствующей 50%, проводится прямая, параллельная оси абсцисс, до пересечения с кумулятой. Затем из точки пересечения указанной прямой с кумулятой опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения является медианой.
Рассчитаем медиану для таблицы 3.2. Медианным будет интервал с границами (100 – 1814). Медиана:

Рассчитаем медиану для таблицы 3.4. Медианным будет интервал с границами (2,17 – 19,52). Медиана:

Графическое построение моды для данного ряда представлено на рисунке 6.4.
Рассчитаем медиану для таблицы 3.6. Медианным будет интервал с границами (5100-22900). Медиана:

Графическое построение моды для данного ряда представлено на рисунке 6.5.

Рис. 6.4. Графическое определение медианы по кумуляте

Рис. 6.5. Графическое определение медианы по кумуляте
РАСЧЕТ КВАРТИЛЕЙ
Квартили представляют собой значения признака, делящие ранжированную совокупность на четыре равновеликие части. Различают квартиль нижний (Q1), отделяющий ¼ часть совокупности с наименьшими значениями признака, и квартиль верхний(Q3), отсекающий ¼ часть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше по величине Q1; 25% единиц будут заключены между Q1 и Q2; 25% - между Q2 и Q3 и остальные 25% превосходят Q3.
Для расчета квартилей по интервальному вариационному ряду используется формула:
 , (6.3)
, (6.3)
где  - квартили;
- квартили;
 - нижняя граница интервала, содержащего квартиль;
- нижняя граница интервала, содержащего квартиль;
 - номер квартиля;
- номер квартиля;
 - частота интервала, содержащего квартиль;
- частота интервала, содержащего квартиль;
 -накопленная частота интервала, предшествующего интервалу, содержащему квартиль.
-накопленная частота интервала, предшествующего интервалу, содержащему квартиль.
Для таблицы 3.2 рассчитаем квартили. Первый квартиль находится в интервале 121 – 1814, накопленная частота которого равна 42 млн.руб. Второй квартиль также находится в интервале 121 – 1814. Третий квартиль лежит в интервале 1814 – 3528 с накопленной частотой 49 млн.руб. Четвертый квартиль находится в интервале 10384 – 12098 с накопленной частотой 60. с учетом этого получим:



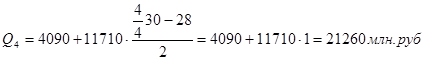
Для таблицы 3.4 рассчитаем квартили. Первый квартиль содержит 15 накопленных частот и входит в интервал (2,78-98,8).

Второй квартиль содержит 30 накопленных частот и входит в интервал (19,52 – 36,87).

Третий квартиль содержит 45 накопленных частот и входит в интервал (71,56 – 88,9).

Четвертый квартиль входит в последний интервал (106,24 – 123,59).

Для таблицы 3.6 рассчитаем квартили. Первый квартиль содержит 7,5 накопленных частот, поэтому входит в интервал (4090-15800).

Второй квартиль содержит 15 накопленных частот, поэтому входит в интервал (4090-15800).

Третий квартиль содержит 22,5 накопленных частот, поэтому входит в интервал (4090-15800).
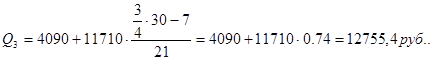
Четвертый квартиль входит в последний интервал (4090-11710).

РАСЧЕТ ДЕЦИЛЕЙ
Децили – варианты, делящие ранжированный ряд на десять равных частей. Первый дециль делит совокупность в соотношении 1/10 к 9/10, второй дециль – в соотношении 2/10 к 8/10 и т.д.
Вычисляются децили по формуле:
 , (6.4)
, (6.4)
где  - децили;
- децили;
 - номер децили;
- номер децили;
 - нижняя граница интервала, содержащего дециль;
- нижняя граница интервала, содержащего дециль;
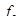 - частота интервала, содержащего дециль;
- частота интервала, содержащего дециль;
 -накопленная частота интервала, предшествующего интервалу, содержащему дециль.
-накопленная частота интервала, предшествующего интервалу, содержащему дециль.
Для таблицы 3.2 рассчитаем 1-й, 3-й, 6-й, 8-й, 9-й дециль. Первый, третий и шестой децили входят в интервал (121-1814), восьмой дециль входит в интервал 1814 – 3528, девятый дециль входит в интервал 5242 – 6956. С учетом этого получим:





Для таблицы 3.4 рассчитаем те же самые децили. Первый и третий децили содержат 6 и 18 накопленных частот соответственно и входят в интервал (2,78– 19,52).
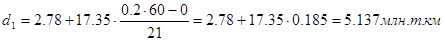

Шестой дециль содержит 36 накопленных частот и входит в интервал (36,67– 54,22).

Восьмой и девятый перцентили содержат 48 и 54 накопленных частот соответственно и входят в интервал (71,56 – 88,9).

Для таблицы 3.6 также рассчитаем децили. Первый дециль содержит 3 накопленные частоты, поэтому входит в интервал (1800-4090).
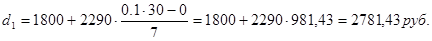
Третий дециль содержит 9 накопленных частот, поэтому входит в интервал (2070-5010).

Шестой дециль содержит 18 накопленных частот, поэтому входит в интервал (4090-15800).

Восьмой дециль содержит 24 накопленных частот, поэтому входит в интервал (15800-21260).

Девятый дециль содержит 27 накопленных частот, поэтому входит в интервал (21260-22900).

РАСЧЕТ ПЕРЦЕНТИЛЕЙ
Значения признака, делящие ряд на сто частей, называются перцентилями. Перцентили вычисляются по формуле:
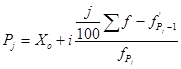 ,(6.5)
,(6.5)
где  - перцентили;
- перцентили;
 - номер перцентиля.
- номер перцентиля.
Для таблицы 3.2 рассчитаем перцентили. 16-й, 23-й, 44-й перцентили входят в интервал (100-1814).
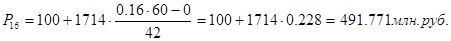

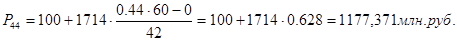
72-й, 77-й, 81-й перцентили входят в интервал (1814 – 35280).
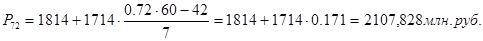
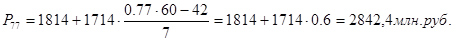

83-й перцентиль содержит 83% накопленных частот и входит в интервал (3528 – 5242).

92-й, 95-й перцентили входят в интервал (6956 – 8670).
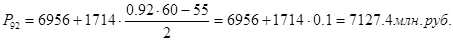

99-й перцентиль входит в интервал (10384 – 12098).

Для таблицы 3.4 рассчитаем 16, 23, 44, 72, 77, 81, 83, 92,95, 99 перцентиль по формуле (6.5):
16-й, 23-й перцентили входят в первый интервал 92,17 – 19,52.


44-й перцентиль содержит 26,4 накопленных частот и входит в интервал (19,52 – 36,87).

72-й, 77-й, 81-й, 83-й перцентили входят в интервал (71,56 – 88,9).




92-й, 95-й перцентили входят в интервал (88,9 – 106,24).


99-й перцентиль входит в интервал (106,24 – 123,59).

Для таблицы 3.6 рассчитаем 16, 23, 44, 72, 77, 81, 83, 92,95, 99 перцентиль по формуле (6.5). 16-й, 23-й перцентили входят в интервал (1800-4090).


44-й, 72-й, 77-й, 81-й, 83-й, 92-й, 95-й перцентили входят в интервал (4090-15800).


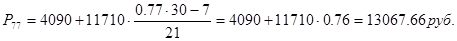





|
из
5.00
|
Обсуждение в статье: РАСЧЕТ И ПОСТРОЕНИЕ СТРУКТУРНЫХ ХАРАКТЕРИСТИК ВАРИАЦИОННОГО РЯ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

