 |
Главная |
Аксиомы и основные задачи статики
|
из
5.00
|
I. Статика. избранные ТЕМЫ
В этом разделе изучаются методы, с помощью которых различные системы сил с целью упрощения можно заменять другими системами, в известном смысле эквивалентными первым. Теоретические результаты, получаемые здесь в виде общих теорем и разнообразных следствий, опираются на ряд положений, принимаемых без логических доказательств. Эти положения (законы, постулаты) принято называть аксиомами статики.
Аксиоматическое построение физических наук в настоящее время общепринято. В основе аксиоматики лежат, как правило, простейшие опыты и наблюдения, сведенные, по возможности, к минимальному числу, а также − присущие нашему сознанию абстрактные обобщения в виде перехода к некоторым предельным (идеальным) схемам для понятий, явлений и процессов.
Приведенные шесть аксиом статики и несколько понятий и определений достаточны для логического построения курса, а главной проверкой справедливости этой научной системы является вся огромная техническая практика в течение тысячелетий.
Здесь используется евклидова геометрия, при этом соответствующие математические аксиомы считаются известными из учебных программ средней школы.
Глава 1. Исходные термины и вводные положения
Основные понятия и определения
Материальная точка − модель материального тела, размерами которого в рамках принятой точности измерения длин (расстояний) пренебрегают, сохраняя массу тела.
“Принятая точность” определяется конкретными задачами движения (равновесия) рассматриваемого тела. Так, судно при определении его положения в океане рассматривается как точка с соответствующими координатами (широта, долгота). То же судно при размещении его у причалов требует учета его размеров.
Абсолютно твердое тело − модель тела, в котором расстояния между любыми двумя точками остаются неизменными. В дальнейшем для краткости абсолютно твердое тело будем называть просто твердым.
Сила − векторная величина, служащая количественной мерой механических взаимодействий между материальными телами (например, действий, воспринимаемых органами чувств: давления, притяжения, сопротивления и т.д.) при различных типах и источниках физических воздействий (упругих, гравитационных, электромагнитных и т.п.) и установленная определенными правилами ее измерения.
Обозначают вектор силы 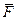 . Действие силы на тело характеризуется точкой приложения силы, направлением действия силы, численной величиной
. Действие силы на тело характеризуется точкой приложения силы, направлением действия силы, численной величиной  .
.
В статике будем рассматривать только постоянные силы, они могут быть измерены динамометром (непосредственно или сравнением с уже измеренными силами).
Совокупность n сил, приложенных к твердому телу, называют системой сил. Обозначают систему сил:  , либо
, либо 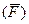 , если число сил, входящих в систему, нас не интересует и может быть произвольным; аналогично для системы сил
, если число сил, входящих в систему, нас не интересует и может быть произвольным; аналогично для системы сил  -
-  . Для простоты записи здесь часто внутренние скобки не используют.
. Для простоты записи здесь часто внутренние скобки не используют.
Различают внешние и внутренние силы. Внешними называют силы, приложенные к рассматриваемому телу со стороны других действующих на него тел.
Внутренними для рассматриваемого тела называют силы, с которыми одна какая-либо его часть действует на другую его часть (но эти силы будут внешними, если за рассматриваемые тела принимают сами эти части).
Уравновешенной системой сил называется такая система, которая, будучи приложена к покоящемуся твердому телу, не нарушает его покоя (заметим, забегая вперед, в динамику, что твердое тело под действием уравновешенной системы сил может и двигаться, и довольно сложно).
Уравновешенную систему сил называют также системой сил, эквивалентной нулю. Обозначение уравновешенной системы сил:
 ∾0.
∾0.
Уравновешивающей системой сил называется система, которая вместе с данной системой образует уравновешенную систему сил. Таким образом, если
 ∾0,то система
∾0,то система  –
–
уравновешивающая система сил для системы  .
.
Две системы сил называются эквивалентными, если они имеют некоторую одну и ту же уравновешивающую систему сил. Обозначают эквивалентные системы сил символом ∾ .
Таким образом,  ∾
∾  ,
,
если  ∾0 и
∾0 и  ∾0.
∾0.
Если система сил эквивалентна одной силе, т.е.  ∾
∾ 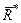 ,то силу
,то силу  называют равнодействующей.
называют равнодействующей.
Примечание. Не всякая система сил имеет равно-действующую (это будет установлено далее).
Аксиомы и основные задачи статики
В качестве аксиом (основных законов) в статике приняты следующие положения.
Аксиома 1. Для того чтобы система двух сил, приложенных к твердому телу, была уравновешенной, необходимо и достаточно, чтобы они были равными по модулю и направленными по одной прямой в противоположные стороны (рис.1.1).

Будем называть такие силы  и
и  противоравными.
противоравными.
Аксиома 2. Не нарушая равновесия твердого тела, к нему можно приложить или отбросить от него любую уравновешенную систему сил.
Из аксиом 1 и 2 нетрудно получить такие следствия:
Следствие 1. Добавление (или отбрасывание) к произвольной системе сил любой эквивалентной нулю системы дает систему, эквивалентную исходной.
Это вытекает из аксиомы 2 и из того, что всякая система сил имеет уравновешивающую, за которую по аксиомам 1 и 2 можно, например, принять систему сил, противоравных данным. В аналитической записи следствие 1:
если  ∾0, то
∾0, то  ∾
∾ 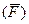 .
.
Справедливо и обратное утверждение.
Следствие 2. Любая система сил, уравновешивающая одну из эквивалентных систем, уравновешивает и другую.
Доказательство. Пусть система  – уравновешивающая система для каждой из систем
– уравновешивающая система для каждой из систем  и
и  ,и пусть
,и пусть  – какая-либо система, уравновешивающая систему
– какая-либо система, уравновешивающая систему  .Тогда по аксиоме 2, добавляя к системе
.Тогда по аксиоме 2, добавляя к системе 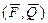 ∾0систему
∾0систему  ∾0, а затем от новой системы
∾0, а затем от новой системы  ∾0отбрасывая
∾0отбрасывая  ∾0, получим
∾0, получим  ∾0, что и требовалось доказать.
∾0, что и требовалось доказать.
Таким образом, не нарушая равновесия твердого тела, любую систему из части действующих на него сил можно заменить эквивалентной системой.
Следствие 3. Две системы сил, порознь эквивалентные третьей, эквивалентны между собой.
Это непосредственно вытекает из определения эквивалентных систем и предыдущего следствия (провести доказательство самостоятельно).
Следствие 4. Системы сил эквивалентны, если они имеют эквивалентные части.
В аналитической записи: если 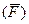 ∾
∾  и
и 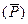 ∾
∾  , то
, то  ∾
∾  .
.
Доказательство. Если  – уравновешивающая система для каждой из систем
– уравновешивающая система для каждой из систем 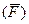 и
и  , а
, а  – для систем
– для систем 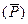 и
и  ,то по аксиоме 2 и следствию 1
,то по аксиоме 2 и следствию 1
 ∾
∾  ∾
∾  .
.
Две системы в этом соотношении справа и слева эквивалентны одной средней системе, следовательно, они эквивалентны, что и требовалось доказать.
Конечно, в этом следствии в частном случае системы 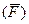 и
и 
 могут быть просто совпадающими.
могут быть просто совпадающими.
Следствие 5. Сила, приложенная к твердому телу, есть вектор скользящий. Другими словами, если силу  , прило-женную к телу в точке A, заменить силой
, прило-женную к телу в точке A, заменить силой  (вектор
(вектор  =
=  ), но приложенной в любой точке B на линии действия
), но приложенной в любой точке B на линии действия  , то
, то  будет эквивалентна
будет эквивалентна  . Действительно, обе эти силы имеют одну и ту же уравновешивающую силу
. Действительно, обе эти силы имеют одну и ту же уравновешивающую силу  ,
,  = -
= -  (рис.1.2).
(рис.1.2).

Аксиома 3. Две силы, приложенные в одной точке тела, имеют равнодействующую, приложенную в той же точке и равную векторной сумме этих двух сил (рис.1.3).
В аналитической записи:
(  ,
,  )∾
)∾ 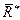 ;
; 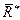 =
=  +
+  .
.
Величина равнодействующей может быть определена по теореме косинусов:
 =
=  =
= 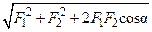 .
.
Эту аксиому называют правилом параллелограмма.
Аксиома 4. Два взаимодействующих тела действуют друг на друга с силами, равными по модулю и направленными по одной прямой в противоположные стороны.
Пусть тела M и N (рис.1.4, а) взаимодействуют между собой в одной точке (контактное взаимодействие).
 |
Тогда  , но система (
, но система ( 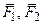 ) не эквивалентна нулю, так как силы приложены к разным телам. Взаимодействие может быть на расстоянии, например, для электрически заряженных тел (рис.1.4, б).
) не эквивалентна нулю, так как силы приложены к разным телам. Взаимодействие может быть на расстоянии, например, для электрически заряженных тел (рис.1.4, б).
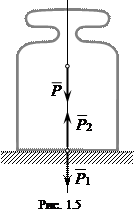 Пример. Рассмотрим тело (гирю), лежащее на столе (рис.1.5). На гирю (если пренебречь ее размерами) дейст-вует сила тяжести
Пример. Рассмотрим тело (гирю), лежащее на столе (рис.1.5). На гирю (если пренебречь ее размерами) дейст-вует сила тяжести  , гиря давит на стол с силой
, гиря давит на стол с силой  , со стороны стола на гирю действует сила
, со стороны стола на гирю действует сила  .
.
Так как гиря находится в равновесии под действием сил  и
и  , то по аксиоме 1 эти силы противоравные. Так как гиря и стол взаимодействуют, то по аксиоме 4 действие (сила
, то по аксиоме 1 эти силы противоравные. Так как гиря и стол взаимодействуют, то по аксиоме 4 действие (сила  )и противодействие (сила
)и противодействие (сила  )направлены по одной прямой в противоположные стороны и равны по модулю, т.е.
)направлены по одной прямой в противоположные стороны и равны по модулю, т.е. 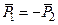 , причем система этих сил не эквивалентна нулю, так как силы приложены к разным телам.
, причем система этих сил не эквивалентна нулю, так как силы приложены к разным телам.
Таким образом, в этом примере все три силы имеют одинаковые модули: P= P1= P2, однако это – разные силы с точки зрения их физического действия на тела.
Аксиома 5. Если под действием некоторой системы сил нетвердое тело находится в равновесии, то при его отвердевании равновесие тела под действием той же системы сохранится.
Эту аксиому называют принципом отвердевания. Здесь не имеется в виду отвердевание как физический процесс. Просто сопоставляют две возможности: действие одинаковых систем сил (предполагая это выполнимым) на деформируемое тело и абсолютно твердое тело.
Пример. Рассмотрим гибкую нерастяжимую нить AB, находящуюся в равновесии под действием сил  и
и  (рис.1.6).
(рис.1.6).
Согласно аксиоме 5, под действием этой системы сил стержень AB также будет находиться в равновесии, что согласуется и с аксиомой 1.
Следует иметь в виду, что если под действием некоторой системы сил твердое тело сохраняет равновесие, то нетвердое тело под действием той же системы сил может не сохранять равновесие.
 |
Так, в том же примере стержень AB сохраняет равновесие и под действием сжимающих сил  и
и  (рис.1.7), что для нити невозможно. Обобщая этот пример, аксиому 5 можно формулировать иначе.
(рис.1.7), что для нити невозможно. Обобщая этот пример, аксиому 5 можно формулировать иначе.
Необходимые и достаточные условия равновесия системы сил, приложенных к твердому телу, являются только необходимыми условиями (но не достаточными!) для равновесия системы сил, приложенных к нетвердому телу.
Основные задачи статики:
1. Приведение заданной произвольной системы сил к простейшему виду.
2. Вывод условий (уравнений) равновесия системы сил, приложенных к твердому телу.
Уравнения равновесия используются для решения разнообразных практических задач.
Связи. Реакции связей
Тела разделяют на свободные и несвободные.
Твердое тело, на перемещения которого не наложено никаких ограничений, называется свободным. В противном случае – несвободным телом. На практике чаще всего встречаются с несвободными телами. Ограничения, наклады-ваемые на перемещения твердого тела, называются связями. Связи, рассматриваемые в статике, обычно осуществляются при помощи других твердых или гибких тел.
Примерами несвободных тел являются: шарик в трубке, гиря на столе, груз, подвешенный на нити и т.д. Несвободное тело взаимодействует с телами, реализующими те или другие связи.
Силы, с которыми эти тела действуют на рассматриваемое несвободное тело, называются реакциями связей. В различ-ных задачах они чаще всего заранее неизвестны.
Силы, действующие на тело и не зависящие от наложения на него связей, называются активными. Например, сила тяжести гири, лежит ли она на столе, подвешена на нити или свободна – активная сила.
Аксиома 6 (аксиома связей). Любое несвободное тело можно рассматривать как свободное, если мысленно отбросить все связи, наложенные на тело, заменяя их действие на тело силами реакции связей.
Моменты сил
В основе различных понятий моментов сил лежит известное из школьного курса физики архимедово правило равновесия рычага под действием сил, стремящихся его повернуть. По этому правилу в условие равновесия рычага входят произведения модулей этих сил на их плечи (расстояния до точки опоры). Основной мерой действия силы на рычаг становится не величина силы непосредственно, а ее произведение на плечо (большую силу можно уравновесить малой, подобрав для второй достаточно большое плечо). Такие произведения называют моментами сил.
Приведенные ниже понятия моментов сил, необходимые и для статики, и для динамики твердых тел, являются обобщениями тех моментов, которые фигурируют в правиле рычага.
Момент силы относительно точки
 Рассмотрим силу
Рассмотрим силу  , приложенную в точке A тела, и произвольно выбранную в пространстве точку O (такую точку
, приложенную в точке A тела, и произвольно выбранную в пространстве точку O (такую точку
часто называют центром момента, рис.1.8;  =
=  ).
).
 Моментом силы
Моментом силы  относительно точки O называется вектор, обозначаемый
относительно точки O называется вектор, обозначаемый  , равный по модулю произведению модуля силы на плечо h (h - длина перпен-дикуляра, опущенного из точки O на линию действия силы), приложенный в точке O и направленный перпендикулярно плоскости, проведенной через вектор
, равный по модулю произведению модуля силы на плечо h (h - длина перпен-дикуляра, опущенного из точки O на линию действия силы), приложенный в точке O и направленный перпендикулярно плоскости, проведенной через вектор  и точку O, так, чтобы наблюдение с конца вектора
и точку O, так, чтобы наблюдение с конца вектора  показывало, что сила стремится повернуть тело вокруг точки О против хода стрелки часов.
показывало, что сила стремится повернуть тело вокруг точки О против хода стрелки часов.
Таким образом, справедливо:
 , (1.1)
, (1.1)
где S DOА B – площадь треугольника OА B.
Если  – радиус-вектор, проведенный из центра момента в точку приложения силы, то для выражения момента справедливо:
– радиус-вектор, проведенный из центра момента в точку приложения силы, то для выражения момента справедливо:
 ,
,  . (1.2)
. (1.2)
Справедливость (1.2) легко подтверждается непосредствен-ными вычислениями для левого и правого векторов.
Таким образом, момент силы относительно точки равен нулю лишь тогда, когда линия действия силы проходит через центр момента (h = 0),  ≠0.
≠0.
Момент силы относительно оси
Пусть дана ориентированная ось Z (ось с выбранным на ней положительным направлением) и произвольная сила  , приложенная в точке A к некоторому телу; через h¢ обозначим плечо силы относительно оси (кратчайшее расстояние между силой и осью, рис.1.9).
, приложенная в точке A к некоторому телу; через h¢ обозначим плечо силы относительно оси (кратчайшее расстояние между силой и осью, рис.1.9).
 |
Обозначим  вектор проекции силы
вектор проекции силы  на плоскость, перпендикулярную оси
на плоскость, перпендикулярную оси  =Пр.oxy
=Пр.oxy  ; F¢=A¢B¢; A¢, B¢ - это проекции точек A, B на эту
; F¢=A¢B¢; A¢, B¢ - это проекции точек A, B на эту 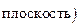 .
.
Моментом силы  относительно оси называется скалярная величина, равная взятому со знаком «+» или «-» произведению модуля вектора
относительно оси называется скалярная величина, равная взятому со знаком «+» или «-» произведению модуля вектора  (проекции силы
(проекции силы  на плоскость, перпендикулярную оси) на плечо h¢.
на плоскость, перпендикулярную оси) на плечо h¢.
Обозначают этот момент  ;
;  (
(  )= ±
)= ±  ∙h¢. Знак «плюс» выбирается, если наблюдение с положительного конца оси z показывает, что вектор
∙h¢. Знак «плюс» выбирается, если наблюдение с положительного конца оси z показывает, что вектор  стремится вызвать поворот тела вокруг оси против хода стрелки часов; знак «минус» – в противоположном случае. Для случая, изобра-женного на рис.1.9,
стремится вызвать поворот тела вокруг оси против хода стрелки часов; знак «минус» – в противоположном случае. Для случая, изобра-женного на рис.1.9,  (
(  )>0.
)>0.
Легко заметить, что момент силы относительно оси равен нулю лишь тогда, когда сила и ось лежат в одной плоскости, т.е. если линия действия силы или пересекает ось (тогда h¢=0), или ей параллельна (тогда F′=0).
Очевидно также (рис.1.9), что  = 2SDOА¢B¢.
= 2SDOА¢B¢.
Можно показать, что справедливо утверждение:
момент силы относительно оси равен проекции на эту ось вектора момента силы относительно произвольной точки О,взятой на этой оси.
В аналитической записи:
 (
(  ) = Пр.OZ
) = Пр.OZ  (
(  ), или
), или  (
(  ) = MOz (
) = MOz (  ).
).
Это утверждение связывает момент силы относительно оси с ее моментом относительно произвольной точки, взятой на этой оси.
Доказательство этого утверждения здесь опущено (предлагается провести его самостоятельно).
|
из
5.00
|
Обсуждение в статье: Аксиомы и основные задачи статики |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

