 |
Главная |
О приведении системы сил к простейшему виду
|
из
5.00
|
(о сложении сил)
Пусть рассматривается система сил ( 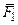 ,…,
,…, 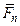 ), приложен-ных к твердому телу. Обсуждаются некоторые вопросы в задаче о сложении сил.
), приложен-ных к твердому телу. Обсуждаются некоторые вопросы в задаче о сложении сил.
Условие существования равнодействующей
 Для того чтобы некоторая система сил имела отличную от нуля равнодействующую, необходимо и достаточно, чтобы главный вектор
Для того чтобы некоторая система сил имела отличную от нуля равнодействующую, необходимо и достаточно, чтобы главный вектор 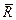 и главный момент
и главный момент 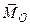 для произвольно выбранного центра приве-дения О были ортогональны.
для произвольно выбранного центра приве-дения О были ортогональны.
Действительно, если равнодействующая 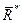 существует, то по теореме эквивалент-ности для любого центра О
существует, то по теореме эквивалент-ности для любого центра О 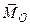 (
( 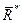 ) =
) = 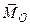 . По определению
. По определению 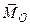 (
( 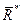 )^
)^ 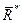 . Значит, и
. Значит, и 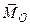 ^
^  (случай
(случай 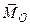 (
( 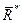 ) = 0, т.е. когда точка О лежит на линии действия
) = 0, т.е. когда точка О лежит на линии действия 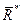 , можно рассматривать как предельный).
, можно рассматривать как предельный).
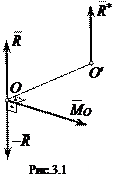
Обратно, если для какого-либо центра О имеем 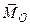 ^
^  , то по теореме о приведении к силе и паре эту пару, имеющую момент
, то по теореме о приведении к силе и паре эту пару, имеющую момент 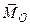 , можем построить так (рис.3.1), чтобы одна из ее сил была равна -
, можем построить так (рис.3.1), чтобы одна из ее сил была равна - 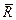 и приложена в О. Тогда вторая сила пары и будет равнодействующей
и приложена в О. Тогда вторая сила пары и будет равнодействующей 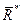 =
= 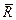 . (При
. (При 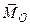 = 0 вопрос решается сразу). Отметим, что если ставить вопрос о существовании «нулевой» равнодействующей, то положительный ответ на него возможен лишь при
= 0 вопрос решается сразу). Отметим, что если ставить вопрос о существовании «нулевой» равнодействующей, то положительный ответ на него возможен лишь при 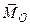 = 0 (т.е. в предельном случае равновесия), так как иначе (
= 0 (т.е. в предельном случае равновесия), так как иначе ( 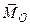 ≠ 0) система сил приводится к паре и равнодействующей не имеет.
≠ 0) система сил приводится к паре и равнодействующей не имеет.
Связь между главными моментами относительно двух
центров. Инварианты
 Пусть
Пусть  и
и 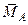 - главный вектор и главный момент неко-торой системы сил относитель-но центра приведения А.
- главный вектор и главный момент неко-торой системы сил относитель-но центра приведения А.
Главный момент той же системы для любого другого центра В (рис.3.2) можно получить в виде суммы: момента 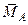 , рассматриваемого как свободный вектор-момент пары, и момента силы
, рассматриваемого как свободный вектор-момент пары, и момента силы  , приложенной в точке А, относительно В. Таким образом:
, приложенной в точке А, относительно В. Таким образом:
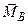 =
= 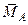 +
+ 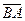 ×
×  . (3.1)
. (3.1)
Если  ≠0, то, умножая скалярно обе части (3.1) на
≠0, то, умножая скалярно обе части (3.1) на  (с учетом (
(с учетом ( 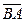 ×
× 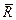 ) ^
) ^ 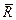 ), получим
), получим 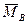
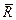 =
= 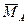
 .
.
Следовательно, для всех центров приведения С величины  и (
и ( 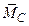
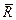 ) являются неизменными (для главного вектора
) являются неизменными (для главного вектора  это очевидно по определению). Это – инварианты данной системы сил.
это очевидно по определению). Это – инварианты данной системы сил.
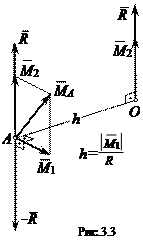 Если же
Если же  =0, то из (3.1) прямо следует
=0, то из (3.1) прямо следует 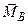 =
= 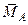 , т.е. инвариантом является сам главный момент, что ясно также из того, что система сил в этом случае приводится к паре.
, т.е. инвариантом является сам главный момент, что ясно также из того, что система сил в этом случае приводится к паре.
Динамический винт
Пусть  и
и 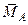 – главный вектор и главный момент для центра А, рис.3.3.
– главный вектор и главный момент для центра А, рис.3.3.
Проводя элементарные преобразования и используя теорему, обратную теореме о сложении пар, заменим пару с моментом 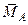 , получающуюся при приведении сил к центру А, двумя парами с моментами
, получающуюся при приведении сил к центру А, двумя парами с моментами 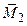 и
и 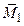 , выбирая
, выбирая 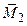 по
по  (или противоположно), а
(или противоположно), а 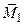 - перпендикулярным
- перпендикулярным  . Эту замену можно делать по правилу сложения пар (разд. 2.5). При этом для пары с моментом
. Эту замену можно делать по правилу сложения пар (разд. 2.5). При этом для пары с моментом 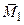 выберем одну из ее сил так, чтобы она была равна –
выберем одну из ее сил так, чтобы она была равна –  и приложена в точке А (как и в разд. 3.1). Тогда после отбрасывания уравновешенной системы сил (
и приложена в точке А (как и в разд. 3.1). Тогда после отбрасывания уравновешенной системы сил (  , –
, –  ), получим силу
), получим силу  , приложенную в точке О, положение которой ясно из рис.3.3 (где отмечены прямые углы), и пару с моментом
, приложенную в точке О, положение которой ясно из рис.3.3 (где отмечены прямые углы), и пару с моментом 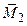 . Этот момент (как свободный вектор) можно перенести в точку О, и он, очевидно, будет равен главному моменту данной системы сил относительно этой точки O:
. Этот момент (как свободный вектор) можно перенести в точку О, и он, очевидно, будет равен главному моменту данной системы сил относительно этой точки O: 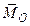 =
= 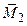 .
.
Система, состоящая из силы  , приложенной в точке О, и пары с моментом
, приложенной в точке О, и пары с моментом 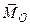 (
( 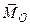 ||
|| 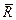 ), называется динамическим винтом. Из рис.3.3 ясно, что
), называется динамическим винтом. Из рис.3.3 ясно, что 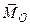 является минимальным по модулю главным моментом системы сил.
является минимальным по модулю главным моментом системы сил.
Прямая, проходящая через точку О, по которой направлены  и
и 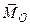 , называется центральной осью системы сил. Конечно, с самого начала центр О мы могли бы выбрать в любой точке центральной оси, и величины
, называется центральной осью системы сил. Конечно, с самого начала центр О мы могли бы выбрать в любой точке центральной оси, и величины  и
и 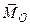 были бы теми же самыми.
были бы теми же самыми.
Краткие выводы
Подытоживая результаты, относящиеся к задаче приведения элементарными преобразованиями произвольной системы сил, действующих на твердое тело, к простейшему виду, получаем для общего случая:
1. Система сил приводится к двум силам, одна из которых приложена в произвольно выбранной точке.
2. Система сил приводится к системе, состоящей из силы, равной главному вектору 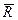 системы и приложенной в произвольно выбранном центре приведения С, и пары, момент которой равен главному моменту
системы и приложенной в произвольно выбранном центре приведения С, и пары, момент которой равен главному моменту 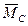 системы сил относительно центра приведения:
системы сил относительно центра приведения:
 =
= 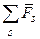 ,
, 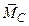 =
= 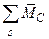 (
( 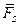 ).
).
3. Система сил приводится к динамическому винту.
Частные случаи. Из 2 следует, что если:
-  = 0, система сил приводится к паре с инвариантным (для всех центров приведения) моментом
= 0, система сил приводится к паре с инвариантным (для всех центров приведения) моментом 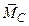 ;
;
- 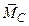 ^
^  или
или 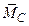 = 0, система сил приводится к равно-действующей
= 0, система сил приводится к равно-действующей 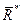 =
= 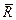 , приложенной в соответствующей точке (разд. 3.1);
, приложенной в соответствующей точке (разд. 3.1);
-  = 0,
= 0, 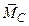 = 0, система сил уравновешена.
= 0, система сил уравновешена.
Упражнение. Показать, что для системы сил, располо-женных в одной плоскости, а также для сил параллельных, будет иметь место один из частных случаев.
Глава 4. Уравнения равновесия системы сил
|
из
5.00
|
Обсуждение в статье: О приведении системы сил к простейшему виду |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

