 |
Главная |
Теорема 2. Приведение к силе и паре
|
из
5.00
|
Всякую неуравновешенную систему сил ( 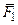 ,…,
,…, 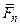 ), приложенную к твердому телу, элементарными преобразо-ваниями можно привести к системе, состоящей из силы, приложенной в произвольно заданном центре приведения О, и пары сил. Причем вектор этой силы равен главному вектору
), приложенную к твердому телу, элементарными преобразо-ваниями можно привести к системе, состоящей из силы, приложенной в произвольно заданном центре приведения О, и пары сил. Причем вектор этой силы равен главному вектору 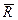 системы сил, а момент этой пары равен главному моменту данной системы относительно этого центра.
системы сил, а момент этой пары равен главному моменту данной системы относительно этого центра.
В аналитической записи:
( 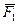 ,…,
,…, 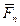 )∾
)∾ 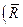 , (
, ( 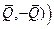 ,
,
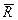 =
= 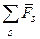 ,
, 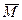 (
(  ,–
,–  )=
)= 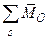 (
( 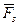 ).
).
 Доказательство. Пусть задана произвольная точка О и неуравновешенная система действующих на твердое тело сил (
Доказательство. Пусть задана произвольная точка О и неуравновешенная система действующих на твердое тело сил ( 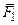 ,…,
,…, 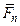 ). Пусть в соответствии с теоремой 1 она приведена к системе двух сил
). Пусть в соответствии с теоремой 1 она приведена к системе двух сил 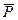 и
и 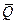 , приложенных соответственно в точках О и А (рис.2.2). Добавив в точке О две противоравные силы
, приложенных соответственно в точках О и А (рис.2.2). Добавив в точке О две противоравные силы  и –
и –  и сложив первую с силой
и сложив первую с силой 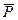 , получим приложенную в О силу
, получим приложенную в О силу 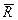 =
= 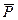 +
+  . Две оставшиеся силы:
. Две оставшиеся силы:  (в точке А) и –
(в точке А) и – 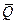 (в точке О) образуют пару (
(в точке О) образуют пару (  , –
, –  ), момент которой, будучи равным моменту силы
), момент которой, будучи равным моменту силы  этой пары относительно точки О, будет по (2.3) равен главному моменту системы (
этой пары относительно точки О, будет по (2.3) равен главному моменту системы ( 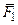 ,…,
,…, 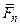 ) относительно О, т.е.
) относительно О, т.е.
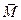 (
(  ,–
,–  )=
)= 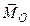 =
= 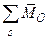 (
( 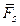 ) и
) и 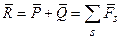 .
.
Доказательство завершено.
Сделаем существенное замечание. Если при приведении системы сил ( 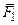 ,…,
,…, 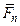 ) к двум силам (
) к двум силам ( 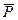 ,
,  ) имела место (при фиксированном центре О) многозначность, то при приведении этой системы к силе и паре сил мы всякий раз будем получать одну определенную силу (она однозначно определяется главным вектором
) имела место (при фиксированном центре О) многозначность, то при приведении этой системы к силе и паре сил мы всякий раз будем получать одну определенную силу (она однозначно определяется главным вектором 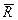 ) и различные пары (
) и различные пары (  , –
, –  ), но с одним и тем же моментом (имеется в виду многозначность сил различных пар; ясно, что по свойству преобразований все такие пары эквивалентны). Он равен неизменному для выбранного центра главному моменту
), но с одним и тем же моментом (имеется в виду многозначность сил различных пар; ясно, что по свойству преобразований все такие пары эквивалентны). Он равен неизменному для выбранного центра главному моменту 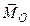 =
= 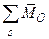 (
( 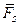 ).
).
Заметим еще, что хотя между векторами моментов
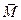 (
( 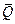 ,–
,– 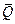 ) и
) и 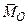 =
= 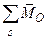 (
( 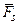 ) есть равенство
) есть равенство 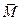 (
( 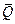 , –
, – 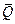 )=
)= 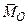 , тем не менее отождествлять эти два вектора не следует, так как справа находится вектор, приложенный строго в центре О, а слева – свободный вектор (момент пары).
, тем не менее отождествлять эти два вектора не следует, так как справа находится вектор, приложенный строго в центре О, а слева – свободный вектор (момент пары).
Перейдем к двум важнейшим теоремам нашего курса.
2.3. Теорема3. Основная теорема статики
Для того чтобы некоторая система сил ( 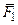 ,…,
,…, 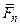 ) была уравновешенной, необходимо и достаточно, чтобы главный вектор этой системы и ее главный момент относительно произвольного центра были равны нулю.
) была уравновешенной, необходимо и достаточно, чтобы главный вектор этой системы и ее главный момент относительно произвольного центра были равны нулю.
Доказательство. 1. Необходимость. Из теоремы о приве-дении любой системы сил к двум силам следует, что ( 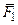 ,…,
,…, 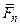 )∾(
)∾( 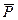 ,
,  ) и
) и
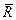 =
= 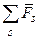 =
= 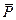 +
+  ; (2.4)
; (2.4)
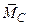 =
= 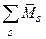 (
( 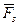 )=
)= 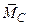 (
( 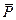 )+
)+ 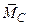 (
(  ), (2.5)
), (2.5)
где С – произвольная точка.
Из условия равновесия ( 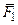 ,…,
,…, 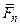 )∾0 по свойству элементарных преобразований получим (
)∾0 по свойству элементарных преобразований получим ( 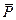 ,
, 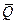 )∾0, и, значит, на основании первой аксиомы силы
)∾0, и, значит, на основании первой аксиомы силы 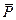 и
и  должны быть системой противоравных сил (в эту систему включаются и нулевые системы). Следовательно, из (2.4) и (2.5) необходимо следует:
должны быть системой противоравных сил (в эту систему включаются и нулевые системы). Следовательно, из (2.4) и (2.5) необходимо следует: 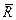 =0,
=0, 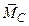 =0.
=0.
2. Достаточность. Пусть для заданной системы справедливо: 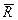 =0,
=0, 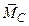 = 0. Тогда из (2.4) и (2.5) получаем
= 0. Тогда из (2.4) и (2.5) получаем
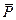 +
+  = 0,
= 0, 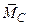 (
( 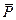 )+
)+ 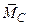 (
(  )= 0,
)= 0,
откуда следует, что 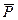 и
и  – силы противоравные и по первой аксиоме уравновешены, а значит, уравновешена и эквивалентная им система сил, т.е.
– силы противоравные и по первой аксиоме уравновешены, а значит, уравновешена и эквивалентная им система сил, т.е.
( 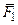 ,…,
,…, 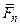 )∾0.
)∾0.
Доказательство закончено. Эта теорема лежит в основе всех уравнений равновесия тел.
2.4. Теорема4. Теорема эквивалентности
Для того чтобы две системы сил были эквивалентными, необходимо и достаточно, чтобы они имели равные главные векторы и равные главные моменты относительно произволь-ного центра.
Доказательство. 1. Необходимость. Если две системы сил эквивалентны
( 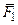 ,…,
,…, 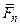 )∾(
)∾( 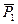 ,…,
,…, 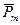 ), (2.6)
), (2.6)
то по определению они имеют одну и ту же уравновеши-вающую систему, за которую можно принять (аксиомы 1, 2 и следствие 2), например, систему сил (– 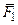 ,…,–
,…,– 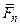 ), противо-равных силам системы (
), противо-равных силам системы ( 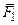 ,…,
,…, 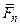 ). Тогда из (2.6)
). Тогда из (2.6)
(– 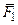 ,…,–
,…,– 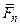 ,
, 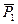 ,…,
,…, 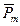 )∾0 (2.7)
)∾0 (2.7)
откуда по основной теореме статики:
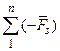 +
+ 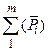 =0; (2.8)
=0; (2.8)
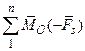 +
+ 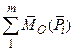 =0, (2.9)
=0, (2.9)
где О – произвольно выбранный центр моментов.
Но для противоравных сил 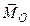 (–
(– 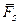 ) = –
) = – 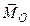 (
( 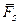 ); из предыдущих равенств получаем:
); из предыдущих равенств получаем:
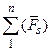 =
= 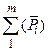 ; (2.10)
; (2.10)
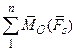 =
= 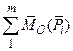 , (2.11)
, (2.11)
что и требовалось доказать.
2. Достаточность. Приняв теперь равенства (2.10) и (2.11) за исходные, мы обратными рассуждениями последовательно убеждаемся в справедливости (2.8) и (2.9), затем (2.7) и, наконец, (2.6), что завершает доказательство теоремы (предлагается провести это доказательство самостоятельно).
|
из
5.00
|
Обсуждение в статье: Теорема 2. Приведение к силе и паре |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

