Оценки дисперсий прогнозов при детерминированных параметрах моделей.

2020-03-19

214

Обсуждений (0)

0.00 из 5.00 0 оценок

Предыдущая 1 234 5 6 7 Следующая

В этой связи, в научной литературе обычно рассматриваются методы оценки дисперсий прогнозов процессов, представленных в виде временных рядов, не учитывающие ошибки оценок коэффициентов, описывающих их моделей. Таким образом, эти методы учитывают специфику моделей с детерминированными параметрами. Очевидно, что эти методы не в полной мере адекватны условиям поставленной задачи. Однако они характеризуются определенной математической строгостью и при небольших ошибках (дисперсиях) коэффициентов моделей позволяют получить относительно точные оценки дисперсий прогнозов, а следовательно, и их доверительных интервалов.

Эти методы можно рассматривать как следствие более общих результатов теории прогнозирования, Г. Валдом, Н.Винером, А. Колмогоровым, П. Уиттлом.[7] В их основе лежит идея представления прогнозного значения рассматриваемого процесса, описываемого моделями типа АРСС(k, m), в виде условного математического ожидания, зависящего от известных в моменты Т, Т–1,... его значений в прошлом, и ошибки, выражаемой текущим и предшествующими значениями “белого шума”. В целях избежания излишней громоздкости рассмотрим эти методы на примере наиболее простых вариантов моделей временных рядов первого порядка.

Модель АР(1).

В соответствии с выражением (1) представим модель АР(1) в виде следующего уравнения:

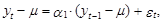
которое для наших целей более удобно представить в следующем виде:

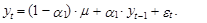(15)

Из выражения (15) вытекает, что прогноз на один шаг вперед, т. е. на момент Т+1, является случайной величиной, определяемой следующим выражением:

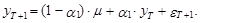(16)

Математическое ожидание этого прогноза имеет следующий вид:

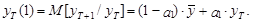(17)

Ошибка такого прогноза определяется как

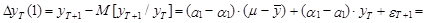
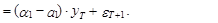(18)

При определении дисперсии прогноза различие между параметром a₁ и его оценкой a₁ во внимание не принимается. В результате имеем

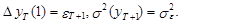(19)

Для момента Т+2 прогноз определяется по следующей схеме:

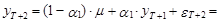
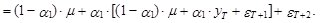(20)

Из выражения (20) следует, что математическое ожидание этого прогноза имеет следующий вид:

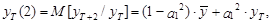
а ошибка D у_T(2) равна

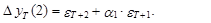(21)

В свою очередь, с учетом независимости e _T₊₂ и e _T₊₁ из выражения (21) следует, что дисперсия прогноза на момент Т+2 оценивается согласно следующему выражению:

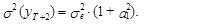(22)

Продолжая схему прогнозирования, определенную выражениями (15)-(22) несложно видеть, что прогноз на l шагов вперед на основе модели АР(1) представляется в следующем виде:

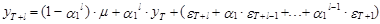(23)

Его математическое ожидание определяется выражением

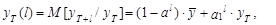(24)

а ошибка и ее дисперсия – соответственно выражениями

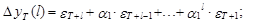(25)

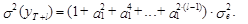(26)

Из выражений (24), в частности, вытекает, что так как ça₁ç<1, то c ростом l математическое ожидание прогноза стремится к математическому ожиданию стационарного процесса

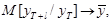
а дисперсия прогноза стремится к дисперсии процесса

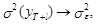
поскольку из выражения (26) следует, что

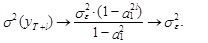(27)

Модель СС(1).[8]

Прогнозируя на момент Т+1 на основе модели СС(1)

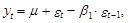
получим следующее прогнозное значение рассматриваемой переменной y:

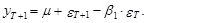(28)

Поскольку математическое ожидание ошибки e _T₊₁ равно нулю, а ее значение в момент времени Т известно, то математическое ожидание такого прогноза равно

(29)

где 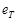– оценка ошибки модели в момент Т.

Из (28) и (29) вытекает, что при неразличимости параметра b₁и его оценки b₁ ошибка такого прогноза равна e _T₊₁.

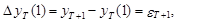(30)

а его дисперсия –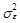

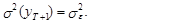(31)

Прогноз на два шага по модели СС(1) определяется выражением

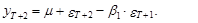(32)

Его математическое ожидание равно –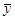

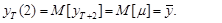(33)

Ошибка такого прогноза равна

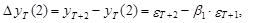(34)

а ее дисперсия определяется следующим выражением:

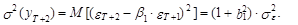(35)

Несложно заметить, что выражение (35) определяет величину дисперсии ошибки прогноза, полученного с использованием модели СС(1), на любое количество шагов вперед, поскольку сама ошибка представляется в следующем виде:

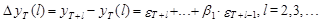(36)

Модель АРСС(1,1).[9]

Модель АРСС(1,1), являющуюся комбинацией рассмотренных выше моделей АР(1) и СС(1), представим в следующем виде:

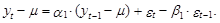
Несложно заметить, что прогнозное значение переменной у_T₊₁ определяется следующим выражением:

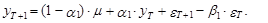(37)

Математическое ожидание такого прогноза с учетом равенства нулю математического ожидания ошибки e _T₊₁ и известного значения ошибки 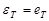равно

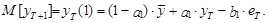(38)

Прогнозируя на момент Т+2, получим следующие выражения, определяющие прогнозное значение рассматриваемой переменной и его математическое ожидание соответственно:

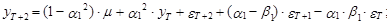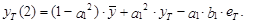(39) (40)

Из выражений (39) и (40) вытекает, что оценка дисперсии прогноза на два шага вперед с использованием модели АРСС(1,1) может быть представлена в следующем виде:

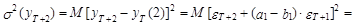
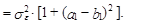(41)

Продолжая последовательно процедуру прогнозирования на момент Т+l, получим следующие выражения прогнозного значения случайной величины и ее математического ожидания:

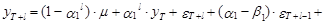
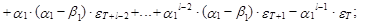(42)

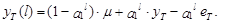(43)

Соответственно из выражений (42) и (43) вытекает, что оценка дисперсии этой ошибки (дисперсии прогноза) может быть определена следующим образом:

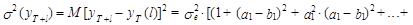
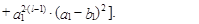(44)

Несложно показать, что l®¥ оценка дисперсии прогноза у_T_+l стремится к следующему пределу:

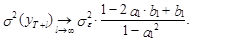(45)

По аналогичной схеме в предположении о детерминированном характере показателей моделей могут быть получены выражения, определяющие оценки дисперсий прогнозов моделей временных рядов и других модификаций, включая модели финансовой эконометрики.