Методика применения авторегрессивных моделей

Использование моделей авторегрессии при моделировании закономерностей реального стационарного процесса второго порядка, допускающего представление в виде дискретного временного ряда его значений, основано на предположении о том, что текущее значение такого процесса может быть выражено в виде линейной комбинации некоторого количества предыдущих его значений и случайной ошибки, обладающей свойствами белого шума.[10]

Общий вид модели авторегрессии k-го порядка – АР(k) может быть выражен следующим уравнением:

(46)

где у_t, у_t–i, i=1,2,... , k – значения переменной у в соответствующие моменты времени; k – порядок модели; a₁,..., a _k  – коэффициенты модели; e _t  – случайная ошибка с нулевым математическим ожиданием, конечной дисперсией и единичной автокорреляционной матрицей, свидетельствующей об отсутствии автокорреляционной связи между рядами ошибки e _t, e _t–1,..., e _t–i,..., т. е. e _t ~N(0, s _e²), Cov(e)=s _e² ×E.

Построение модели АР(k) типа (46), адекватной реальному временному ряду у_t, t=1,2,..., Т, предполагает решение двух взаимосвязанных задач: определения рационального порядка модели (величины k) и оценки значений ее коэффициентов. Рассмотрим сначала общие подходы к оценке параметров модели типа (46).

Без ограничения общности будем предполагать, что математическое ожидание ряда у_t равно нулю, т. е. M[у_t ]=0. В противном случае вместо переменной у_t в выражении (46) можно рассмотреть центрированную переменную , , где – оценка M[у_t ]. Легко видеть, что M[  ] = 0.

Из выражения (46) непосредственно следует, что параметры модели a₁,..., a _k могут быть выражены через коэффициенты автокорреляции. Чтобы показать это, умножим выражение (6.36) под знаком математического ожидания на переменную у_t–i, i=1,2,..., k. Получим

(47)

где M[у_t-i, у_t--j] – математическое ожидание произведения двух центрированных переменных у_t–i, у_t–j, представляющих собой их ковариацию g _r, на практике оцениваемую по формуле

(48)

где r=i – j , i ³ j.

В результате для i=1,2,..., k вместо (47) можно записать

(49)

Выражение (49) получено в предположении, что M[у_t-i, e _t]=0 при i>0, так как e _t  – случайная величина со свойствами “белого шума”, не имеющая корреляционной связи с предшествующими моменту t значениями рассматриваемого процесса у_t. Разделив левую и правую части выражения (49) на дисперсию процесса у_t s _у²=g ₀, получим следующее выражение:

(50)

которое связывает коэффициенты автокорреляции процесса у_t и коэффициенты модели АР(k).

Подставив в (50) вместо истинных значений коэффициентов автокорреляции r _i процесса у_t  их выборочные оценки r₁, r₂,..., последовательно для i=1,2,..., k, получим следующую систему линейных уравнений:

(51)

в которой известными являются оценки коэффициентов автокорреляции r₁, r₂,..., r_k, а неизвестными – оценки коэффициентов модели АР(k) a₁ , a₂ ,..., a_k.

Систему (51) называют уравнениями Юла-Уокера, а полученные на ее основе значения a₁, a₂,..., a_k – оценками коэффициентов модели авторегрессии АР(k) Юла-Уокера. Напомним, что эти оценки могут быть получены, например, с использованием определителей, либо на основе векторно-матричной формы записи системы (51).

На основе определителей оценки Юла-Уокера получают в следующем виде:

(52)

где D – определитель системы (6.41).

(53)

D_i  – определитель, получаемый из определителя D путем замены его i-го столбца на столбец, состоящий из коэффициентов автокорреляции, образующих левую часть системы (51) – r₁, r₂,..., r_k.

В векторно-матричной форме записи систему (51) можно переписать в следующем виде:

r = R×a,                                    (54)

где r – вектор-столбец известных оценок коэффициентов автокорреляции с первого по k-й включительно, r=(r₁, r₂, ..., r_k)¢; a – вектор-столбец неизвестных оценок параметров модели, a=(a₁, a₂,..., a_k)¢; R – матрица, составленная из оценок коэффициентов автокорреляции, определитель которой выражен формулой (53).

Непосредственно из выражения (54) вытекает, что неизвестные оценки коэффициентов модели авторегрессии определяются как

a = R^–1×r.                                    (55)

Теоретически оценки Юла-Уокера[11] должны обладать свойствами несмещенности и эффективности. Однако, на практике, в моделях авторегрессии большого порядка эти свойства могут не подтверждаться. Особенно это относится к свойству несмещенности. Как и в моделях с лаговыми зависимыми переменными, смещенность в оценках коэффициентов моделей авторегрессии может быть обусловлена существующей зависимостью между сдвинутыми рядами рассматриваемой переменной у_t–1, у_t–2 и ошибкой e_t. Этой возможной зависимостью при построении системы уравнений Юла-Уокера обычно пренебрегают, полагая e _t   белым шумом.

Неэффективность оценок может быть вызвана плохой обусловленностью матрицы R, что, как правило, является свидетельством зависимости уже между рядами у_t–1, у_t–2,... .

Вместе с тем, при небольших порядках модели (k =1,2,3) оценки Юла-Уокера обычно являются достаточно “хорошими”. В крайнем случае их можно рассматривать как первое приближение к “оптимальным” оценкам, которые могут быть получены путем уточнения оценок Юла-Уокера на основе использования более мощных методов оценивания, например, нелинейных.

Качество оценок Юла-Уокера может быть проверено путем исследования свойств ряда ошибки e _t, t=1,2,..., Т. Если ее свойства близки к характеристикам “белого шума”, то оценки Юла-Уокера можно считать “достаточно хорошими”. Об этом, в частности, может свидетельствовать критерий Дарбина-Уотсона, значение которого должно лежать примерно в интервале от 1 до 3[12].

Для этих целей могут использоваться и другие мощные критерии, например, Бартлетта, Тейла.

Обоснование целесообразности применения моделей авторегрессии. Целесообразность использования моделей авторегрессии в анализе закономерностей временного ряда обычно устанавливается на основе сопоставления двух дисперсий – дисперсии исходного процесса s _у² и дисперсии ошибки модели s _e². Для того чтобы выявить взаимосвязь между двумя этими характеристиками положим, что в формуле (49) i=0. Тогда это выражение можно переписать в следующем виде:

(56)

где g₀=s _у², g _i – i-й коэффициент автоковариации.

Последнее слагаемое в правой части выражения (56) получено путем замены в выражении (47) в произведении M[y_t××e _t] переменной y_t на ее модель (46). Поскольку ряды у_t–1,..., у_t–k    и e_t являются независимыми, то это произведение оказывается равным s _e². Далее, поскольку g _i =r _i×g₀, то выразив все g _i, i=1,2,..., k через g₀и перенеся слагаемые с g₀в левую часть, из выражения (56) получим

(57)

Подставив в (57) вместо r _i  значения оценок коэффициентов автокорреляции r_i и вместо параметров модели a _i их оценки а_i, i=1,2,... , k, найдем величину соотношение между дисперсией процесса s _у² и дисперсией ошибки описывающей этот модели авторегрессии (белого шума) s _e².

(58)

Модель авторегрессии считается “достаточно хорошей”, если s _у²>>s _e², т. е. когда дисперсия ошибки модели много меньше дисперсии процесса. В этом случае использование модели при описании процесса y_t  позволяет значительно снизить его неопределенность, выражаемую через дисперсию s _у². Здесь также следует отметить, что в моделях временных ярдов нельзя ожидать значительного уменьшения дисперсии ошибки s _e²   по сравнению с дисперсией процесса s _у², как это имело место в моделях “классической” эконометрики, где отношение s _у²/s _e²  нередко превосходит несколько десятков.

Чтобы показать это, рассмотрим свойства наиболее часто используемых в практике финансовых исследований моделей авторегрессии первого и второго порядков.

Модели АР(1) и АР(2).[13]

Модель авторегрессии первого порядка АР(1) записывается в следующем виде:

(59)

Легко видеть, что система Юла-Уокера в этом случае сводится к одному уравнению, непосредственно определяющему оценку a₁ коэффициента a₁

a₁=r₁.                                     (60)

Из выражения (58) вытекает, что

(61)

Поскольку ½r₁½<1, то из (61) следует, что, например, при r₁=0,9 s _e²»0,2×s _у². Это означает, что использование расчетных значений процесса y_t, определяемых по формуле  вместо среднего значения временного ряда  позволит повысить точность предсказания его значений в пять раз (если в качестве меры точности рассматривать показатель дисперсии). В этом случае соотношение между среднеквадратическими ошибками s _у и s _e  составит примерно 2,3. Из выражения (61) легко также видеть, что с ростом абсолютного значения r₁точность описания процесса y_t моделью авторегрессии первого порядка увеличивается, а с его снижением – падает.

Модель авторегрессии второго порядка – АР(2) представляется в виде следующего уравнения:

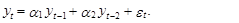(62)

Система уравнений Юла-Уокера в этом случае состоит из двух уравнений

(63)

Выразив a₁ и a₂ через коэффициенты автокорреляции с использованием, например, метода определителей (52), получим

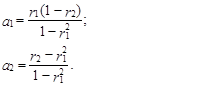(64)

Из выражения (58) непосредственно вытекает, что в этом случае соотношение между дисперсиями исходного процесса y_t  и ошибкой модели e _t определяется следующим выражением:

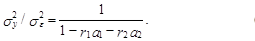(65)

На практике и в случае АР(2) соотношение между s _у² и s _e² обычно не превосходит 5:1. В этом смысле следует отметить, что по сравнению с эконометрическими моделями, где это соотношение достигает 50 к 1 и даже 100 к 1, модели авторегрессии, на первый взгляд, не обладают высокой точностью описания рассматриваемых процессов. Однако не следует забывать, что в “классической” эконометрике зависимая переменная y_t не обладает свойством стационарности и она характеризуется гораздо большей изменчивостью (и, как следствие, дисперсией) по сравнению со стационарным временным рядом. Поэтому адекватные рассматриваемому процессу многофакторные эконометрические модели могут значительно уменьшить остаточную изменчивость (дисперсию ошибки) по сравнению с исходной (дисперсией процесса), но при этом изменчивость ошибки может оставаться относительно большой.

Модели же авторегрессии, как и другие модели стационарных временных рядов, как бы уточняют” исходный процесс y_t, как правило, благодаря свойству стационарности не отличающийся значительной изменчивостью. Вследствие этого у этих моделей имеется лишь незначительный резерв для уменьшения исходной дисперсии s _у² по сравнению с многофакторными эконометрическими моделями, описывающими нестационарные процессы.

Автокорреляционная функция моделей авторегрессии.

По аналогии с реальными стационарными процессами, автокорреляционные функции могут быть сформированы и для их теоретических аналогов – моделей авторегрессии.[14] Заметим, что значения коэффициентов автокорреляции модели k-го порядка связаны между собой соотношением (50). Несложно заметить, что для модели авторегрессии первого порядка это соотношение приводит к следующей зависимости между коэффициентами автокорреляции:

(66)

В самом деле, из выражения (59)) для i=2 имеем r₂=a₁r₁ и, учитывая, что a₁=r₁, получим r₂=r₁², аналогично, для i=3 имеем r₃=a₁r₂=r₁³ и т.д. Если учесть, что ôr₁ô<1, то нетрудно заметить, что модули значений коэффициентов автокорреляции модели АР(1) авторегрессии уменьшаются по экспоненте с ростом сдвига i.

Можно показать, что поскольку модель авторегрессии второго порядка является стационарным процессом, то ее автокорреляционная функция представляет собой либо затухающую экспоненту, либо затухающую синусоиду. В первом случае абсолютные значения коэффициентов автокорреляции r _i  с ростом i уменьшаются согласно следующей зависимости:

(67)

где d – положительный коэффициент экспоненциальной зависимости, отличный от единицы, d ¹1.

Заметим, что для модели АР(1) этот коэффициент равен единице (см. выражение (66)).

Во втором случае значения коэффициентов r _i аппроксимируются функцией следующего вида:

(68)

где f и F – параметры синусоиды (частота и фаза соответственно), рассчитываемые на основе значений коэффициентов модели. В частности,  

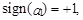если a₁ >0 и 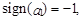если a₁ <0.