 |
Главная |
Методика применения моделей скользящей средней в эконометрике
|
из
5.00
|
В моделях скользящего среднего текущее значение стационарного случайного процесса второго порядка yt представляется в виде линейной комбинации текущего и прошедших значений ошибки e t, e t–1, e t–2,... , по своим свойствам соответствующей “белому шуму”[15]. Такое представление может быть выражено следующим уравнением (модель скользящего среднего порядка m – СС(m)):
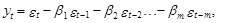 (69)
(69)
где b1, b2,... , b m – параметры модели.
В соответствии с определением белого шума ошибка e t характеризуется следующими свойствами:
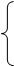 M[e t]=0, D(e t)=s e2=const,
M[e t]=0, D(e t)=s e2=const,
g i=M[e t , e t–i ] =  (70)
(70)
Вследствие этого и автокорреляционная функция белого шума имеет очень простую форму
r i(e)=1, i=0; r i(e)=0, i¹0. (71)
С учетом свойств ошибки e t несложно построить автокорреляционную функцию модели СС(т), определяемой выражением (69). Ее коэффициент ковариации i-го порядка определяется следующим образом:
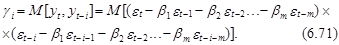 (72)
(72)
При i=0 выражение (72) представляет собой дисперсию процесса yt, которая в силу свойства (70) выражается через коэффициенты модели СС(т) b i, i=1, 2,..., т; и дисперсию ошибки s e2 следующим образом:
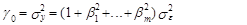 (73)
(73)
Для i=1 из (73) получим, что первый коэффициент ковариации определяется выражением
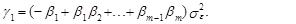 (74)
(74)
Для произвольного i имеем
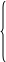
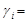
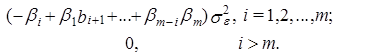 (75)
(75)
Из соотношения (75) вытекает, что автокорреляционная функция модели СС(т) становится равной нулю после задержки т (обрывается на задержке т).
С учетом выражений (73) и (75) несложно также заметить, что коэффициенты автокорреляции модели скользящего среднего т-го порядка – СС(т) определяются через ее параметры b i, i=1, 2,..., т; следующим образом:
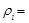
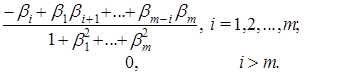 (76)
(76)
Система из т уравнений (76), сформированных для i=1,2,..., т может служить основой для получения оценок b1, b2,... , bm неизвестных параметров модели СС(т) – b1, b2,... , b m. Для этого необходимо подставить в каждое ее уравнение вместо значений коэффициентов автокорреляции r1,..., r m рассматриваемого процесса yt их рассчитанные оценки r1,..., rm.
Однако в отличие от уравнений Юла-Уокера эта система нелинейная и ее решение требует использования специальных итеративных процедур расчетов за исключением наиболее простой модели СС(1). Она представляется следующим выражением:
 (77)
(77)
Из (73) следует, что дисперсии процесса s у2 и ошибки этой модели s e2 связаны следующим соотношением:
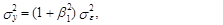 (78)
(78)
а ее единственный отличный от нуля первый коэффициент автокорреляции выражается через коэффициент модели как
 (79)
(79)
Из соотношения (79) несложно получить квадратическое уравнение относительно оценки b1 неизвестного параметра b1
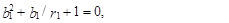 (80)
(80)
где r1 – оценка коэффициента автокорреляции первого порядка процесса yt, т. е. r1.
В свою очередь, из (80) следует, что существуют два решения этого уравнения, связанные между собой следующим соотношением:
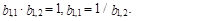 (81)
(81)
Условию стационарности процесса yt удовлетворяет только решение b по абсолютной величине меньшее единицы. Оно может быть получено из следующего выражения:
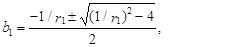 (82)
(82)
при условии, что
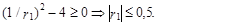 (83)
(83)
Из (83) следует, что модели скользящего среднего первого порядка могут применяться только для описания процессов с автокорреляционной функцией, обрывающейся после первой задержки и коэффициентом автокорреляции по абсолютной величине не превышающем 0,5. Из соотношения (83) также вытекает, что данные модели способны лишь незначительно уточнить рассматриваемый процесс yt, поскольку согласно (78) максимальное соотношение между его дисперсией и дисперсией ошибки не превосходит 1,25
s у2/s e2< 1,25 , (84)
т. е. относительный выигрыш в точности не превосходит 25% для дисперсий (чуть более 11% для среднеквадратических ошибок).
В заключение этого раздела приведем основные результаты для модели скользящего среднего второго порядка – СС(2). Ее уравнение в общем виде записывается следующим образом:
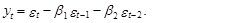 (85)
(85)
Из (73) непосредственно вытекает, что дисперсии процесса s у2 и ошибки s e 2 связаны следующим соотношением:
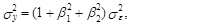 (86)
(86)
а ее автокорреляционная функция определяют значения коэффициентов автокорреляции, связанные с параметрами модели следующими соотношениями:
 (87)
(87)
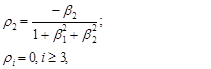
из которых могут быть найдены оценки коэффициентов модели b1 и b2 при известных оценках коэффициентов автокорреляции процесса yt – r1 и r2.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Многие финансово-экономические показатели наряду с устойчивой тенденцией к росту или уменьшению подвержены сезонным колебаниям. Такие процессы удовлетворительно моделируются временными рядами, включающими в себя как тренд, так и сезонную компоненту (тренд - сезонными временными рядами). Примером такого экономического показателя может служить стоимость акции, растущая в цене в течение ряда лет, по которой ежегодно выплачиваются (например, в начале года) дивиденды. Так как стоимость акции из года в год растет, мы имеем восходящий долгосрочный тренд. Однако, в начале года стоимость акции ниже, чем в конце предыдущего года, так как ее стоимость к концу года включает в себя накопившиеся за год дивиденды. Их получит владелец ценной бумаги, после чего дивиденды уже не входят в стоимость акции, и цена ее уменьшается.
Для краткосрочного прогнозирования таких процессов можно использовать адаптивные модели с сезонной компонентой, например, модель Хольта-Уинтерса.[16]
2.1. Построение модели Хольта-Уинтерса.
Рассмотрим данный метод на примере роста стоимости акции. Временной ряд, характеризующий стоимость акции за 16 кварталов (4 года) приведен в табл. 2.1. Нас интересуют прогнозные значения цен на эти акции в 1-4 кварталах пятого года.
Таблица 2.1. Цена акции за 16 кварталов (4 года)
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Y(t) | 304 | 320 | 334 | 347 | 323 | 342 | 365 | 375 |
| t | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Y(t) | 342 | 365 | 378 | 399 | 363 | 388 | 419 | 418 |
Будем считать, что зависимость между компонентами тренд-сезонного временного ряда мультипликативная. Мультипликативная модель Хольта-Уинтерса с линейным ростом имеет следующий вид:
Yp(t+k) = [ a(t) + k*b(t) ] * F(t+k-L) (2.1)
где k – период упреждения,
Yp( t )- расчетное значение экономического показателя для t-го периода;
a(t) , b(t) и F(t) коэффициенты модели, они адаптируются, уточняются по мере перехода от членов ряда с номером t-1 к t;
F(t+k-L) – значение коэффициента сезонности того периода, для которого рассчитывается экономический показатель. L – период сезонности (для квартальных данных L=4, для месячных L=12). Таким образом, если по формуле 3.1 рассчитывается значение экономического показателя, например, за второй квартал, то F(t+k-L) как раз будет коэффициентом сезонности второго квартала предыдущего года.
Уточнение (адаптация к новому значению параметра времени t) коэффициентов модели производится с помощью формул:
a(t) = 1* Y(t)/F(t-L) + (1 - 1) * [ a(t-1)+b(t-1) ] (2.2)
b(t) = 3* [ a(t) – a(t-1) ] + (1 - 3) * b(t-1) (2.3)
F(t)= 2*Y(t)/a(t)+(1- 2)*F(t-L) (2.4)
Параметры сглаживания a 1 , a 2иa 3подбирают путем перебора с таким расчетом, чтобы расчетные данные наилучшим образом соответствовали фактическим (то есть чтобы обеспечить удовлетворительную адекватность и точность модели).
Из формул 2.1 – 2.4 видно, что для расчета a (1) и b (1) необходимо оценить значения этих коэффициентов для предыдущего период времени (то есть для t =1-1=0). Значения a (0) и b (0) имеют смысл этих же коэффициентов для четвертого квартала года, предшествующего первому году, для которого имеются данные в табл. 3.1.
Для оценки начальных значений a(0) и b (0) применим линейную модель к первым 8 значениям Y(t) из табл. 3.1. Линейная модель, имеет вид:
Yp(t) = a(0) + b (0)*t (2.5)
Метод наименьших квадратов дает возможность определить коэффициенты линейного уравнения a(0) и b (0) по формулам (2.6-2.9):

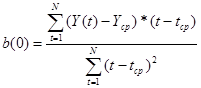 (2.6)
(2.6)
a (0) = Ycp - b (0)* t ср (2.7)
 |
Применяя линейную модель к первым 8 значениям ряда из таблицы 2.1. (то есть к данным за первые 2 года), находим значения a(0)= 300,05, b(0)= 8,60.
Уравнение (2.5) с учетом полученных коэффициентов имеет вид: Yp(t) = 300,05 + 8,60*t.Из этого уравнения находим расчетные значения Yp(t) и сопоставляем их с фактическими значениями (см. табл.3.2). Такое сопоставление позволяет оценить приближенные значения коэффициентов сезонности 1 – 4 кварталов F (-3), F (-2), F (-1) и F (0) для года, предшествующего первому году, по которому имеются данные в табл. 2.1. Эти значения необходимы для расчета коэффициентов сезонности первого года F(1), F(2), F(3), F(4) и других параметров модели Хольта-Уинтерса по формулам 2.1-2.4.
Таблица 2.2. Сопоставление фактических данных Y(t) и рассчитанных по линейной модели. значений Yp(t)
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Y(t) | 304 | 320 | 334 | 347 | 323 | 342 | 365 | 375 |
| Yр(t) | 308.65 | 317.25 | 325.85 | 334.45 | 343.05 | 351.65 | 360.25 | 368.85 |
Коэффициент сезонности есть отношение фактического значения экономического показателя к рассчитанному по линейной модели. Поэтому в качестве оценки коэффициента сезонности первого квартала F (-3) может служить отношение фактических и расчетных значений Y ( t ) первого квартала первого года, равное Y (1)/ Yp (1) и такое же отношение для первого квартала второго года (то есть за пятый квартал t=5) Y (5)/ Yp (5). Для окончательной, более точной оценки этого коэффициента сезонности можно использовать среднее арифметическое значение этих двух величин
F (-3)=[ Y (1)/ Yp (1)+ Y (5)/ Yp (5)]/2=[304/308,67+323/343,05]/2= =[0,9849+0,9416]/2=0,9633
Аналогично находим оценки коэффициенты сезонности для второго, третьего и четвертого кварталов:
F(-2) = [ Y(2)/Yp(2) + Y(6)/Yp(6) ] / 2 = 0,9907
F(-1) = [ Y(3)/Yp(3) + Y(7)/Yp(7) ] / 2 = 1,0191
F (0) = [ Y (4)/ Yp (4) + Y (8)/ Yp (8) ] / 2 = 1,0271
Oценив значения a(0), b (0),а такжеF(-3), F(-3), F(-3) и F(0),можно перейти к построению адаптивной мультипликативной модели Хольта-Уинтерса с помощью формул (2.1-2.4).
Путем перебора возможных значений параметров сглаживания, было установлено, что лучшими являются a 1 = 0,3; a 2 = 0,6; a 3 = 0,3.
Рассчитаем значения Yp ( t ), a ( t ), b ( t ) и F ( t ) для t =1.
Из уравнение 3.1, полагая t =0, k =1 находим Yp (1):
Yp(0+1)=Yp(1)=[a(0)+1*b(0)]*F(0+1-4)=[a(0)+1*b(0)]*F(-3)=
=[ 300,05+ 1* 8,60 ] * 0,9633 = 297.32
Из уравнение 2.2-2.4, полагая t =1 находим:
a(1)= 1*Y(1)/F(-3)+(1- 1)*[a(0)+b(0)]=0.3*304/0,9633+(1-0.3)*[300,05+8,60 ]=310.73
b(1)= 3*[a(1)–a(0)]+(1- 3)*b(0)=0.3*[310.73-300,05]+(1-0.3)*8,60=9.22
F(1)= 2*Y(1)/a(1)+(1- 2)*F(-3)=0.6* 304/310.73+(1-0.6)* 0,9633=0.9723
Аналогично рассчитаем значения Yp ( t ), a ( t ), b ( t ) и F ( t ) для t =2
Yp(2)=[ a(1) + 1 * b(1) ]*Fo(-2)=[ 310.73+1*9,22 ] * 0,9907=316.97
a(2)= 1*Y(2)/F(-2)+(1- 1)*[a(1)+b(1)]=0.3*320/0,9907+0.7*[310,73+9.22]=320.87
b(2)= 3*[a(2)–a(1)]+(1- 3)*b(1)=0.3*[ 320.87-310.73]+0.7* 9.22=9.50
F(2)= 2*Y(2)/a(2)+(1- 2)*Fo(-2)=0.6* 320/320.87+0.4* 0,9907=0.9947
для t=3
Yp(3)=[ a(2)+1 * b(2)]*Fo(-1)=[320.87+1*9,50 ]*1.0191=3369
a(3)= 1*Y(3)/F(-1)+(1- 1)*[a(2)+b(2)]=0.3*334/1.0191+0.7*[320,87+9.50]=329.58
b(3)= 3*[a(3)–a(2)]+(1- 3)*b(2)=0.3*[ 329.58-320.87]+0.7* 9.50=9.26
F(3)= 2*Y(3)/a(3)+(1- 2)*F(-1)=0.6*334/329.58+(1-0.6)*1.0191=1.0157
для t=4
Yp(4)=[ a(3)+1*b(3)]*F(0)=[329.58+1*9,26 ]*1.0271=348.02
a(4)= 1*Y(4)/F(0)+(1- 1)*[a(3)+b(3)]=0.3*347/1.0271+0.7*[329,58+9.26]=338.54
b(4)= 3*[a(4)–a(3)]+(1- 3)*b(3)=0.3*[338.54-329.58]+0.7* 9.26=9.17
F(4)= 2*Y(4)/a(4)+(1- 2)*F(0)=0.6* 347/338.54+0.4*1.0271=1.0258
для t=5
Yp (5)=[ a (4)+1* b (4)]* F (1)=[338.54+ 1*9,17]*0.9723=338.08
Обратим внимание на то, что здесь и в дальнейшем используются коэффициенты сезонности F(t-L), уточненные в предыдущем году (L=4).
a(5) = 1* Y(5)/F(1)+(1- 1)*[a(4)+b(4)]=0.3*323/0.9723+(1-0.3)*[338.54+9.17 ]=343.06
b(5) = 3*[a(5)–a(4)] +(1- 3)*b(4)=0.3*[343.06-338.54]+(1-0.3)*9.17=7.77
F(5)= 2*Y(5)/a(5)+(1- 2)*F(1)=0.6* 323/343.06+(1-0.6)* 0.9723=0.9538
Продолжая аналогично для t=6,7,8,…,16, строят модель Хольта-Уинтерса (см. табл. 2.3). Максимальное значение t , для которого можно находить коэффициенты модели, равно количеству имеющихся данных по экономическому показателю Y ( t ). В нашем примете данные приведены за 4 года, то есть за 16 кварталов. Максимальное значение t равно 16. Ошибкой является попытка студента рассчитать или использовать коэффициенты a ( t ), b ( t ) для t > 16.
Таблица 2.3. Модель Хольта-Уинтерса
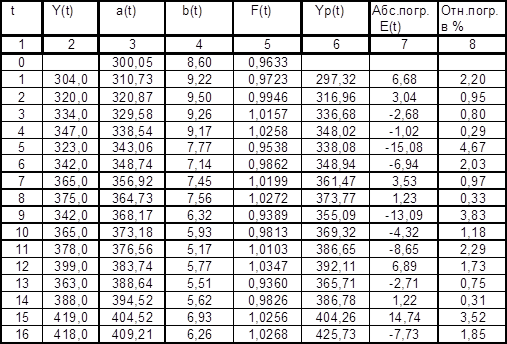
|
из
5.00
|
Обсуждение в статье: Методика применения моделей скользящей средней в эконометрике |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

