Проверка условия адекватности.

Для того, чтобы модель была адекватна исследуемому процессу ряд остатков E(t) должен обладать свойствами 

а) случайности;

б) независимости последовательных уровней;

в) нормальности распределения.[17]

Проверка случайности уровней. Проверку случайности уровней остаточной компоненты (гр. 2 табл. 2.4) проводим на основе критерия поворотных точек. Для этого каждый уровень ряда E(t) сравниваем с двумя соседними. Если он больше (либо меньше) обоих соседних уровней, то точка считается поворотной и в гр. 3 табл. 3.4 для этой строки ставится 1, иначе в гр. 3 ставится 0. В первой и последней строке гр. 3 табл. 3.4 ставится прочерк или иной знак, так как у этого уровня нет двух соседних уровней.

Таблица 2.4. Промежуточные расчеты для оценки адекватности модели[18]

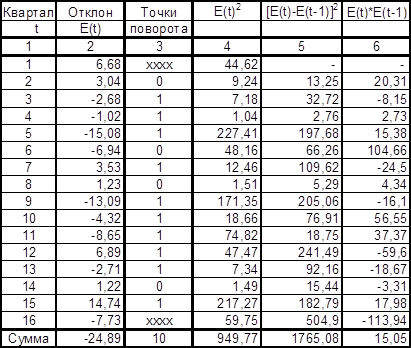Общее число поворотных точек в нашем примере равнор = 10.

Рассчитаем значение  q:

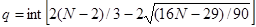Функция int означает, что от полученного значения берется только целая часть. При N = 16   

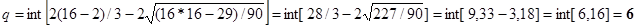
Если количество поворотных точек р больше q, то условие случайности уровней выполнено. В нашем случае р = 10, q = 6, значит условие случайности уровней ряда остатков выполнено.

Проверка независимости уровней ряда остатков (отсутствия автокорреляции). Проверку проводим двумя методами:

а) по d-критерию Дарбина-Уотсона;

б) по первому коэффициенту автокорреляции r(1).

Проверка по d-критерию Дарбина-Уотсона. Для проверки по d-критерию Дарбина-Уотсона рассчитаем значение d

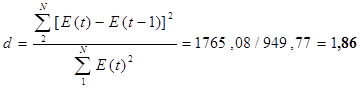
Примечание. В случае если полученное значение больше 2, значит имеет место отрицательная автокорреляция. В таком случае величину d уточняют, вычитая полученное значение из 4.

Полученное (или уточненное) значение d сравнивают с табличными значениями d 1и d 2. Таблицу значений d 1 и d 2 можно найти, например, в литературе[19]. Для нашего случая d 1=1.08, а d 2=1.36.

Если 0<d<d1, то уровни автокоррелированы, то есть зависимы, модель неадекватна;

Если d1<d<d2, то критерий Дарбина –Уотсона не дает ответа на вопрос о независимости уровней ряда остатков. В таком случае необходимо воспользоваться другими критериями (например, проверить независимость уровней по первому коэффициенту автокорреляции).

Если d2<d<2 , то уровни ряда остатков являются независимыми.

В нашем случае это условие выполнено, так как 1.36< 1.86<2, следовательно, уровни ряда E ( t ) независимы.

Проверка по первому коэффициенту автокорреляции r(1).

Рассчитаем r(1) по формуле

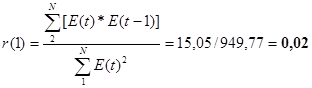
Если модуль рассчитанного значения первого коэффициента автокорреляции меньше критического значения | r(1) | < r_таб , то уровни ряда остатков независимы. Таблицу значений r_таб можно найти, например, в[20]. Для нашей задачи критический уровень r_таб= 0,32. Имеем:

| r (1) | = 0,02 < r _таб = 0,32       значит уровни независимы.

Проверка соответствия ряда остатков нормальному распределению определяем по RS – критерию. Рассчитаем значение RS:

                    RS = ( E_max – E_min ) / S

где E_max - максимальное значение уровней ряда остатков E(t)

  E_min - минимальное значение уровней ряда остатков E(t) (см. гр. 2 табл. 2.4.)

S - среднее квадратическое отклонение

E_max =14,74 E_min = - 15.08 , E_max – E_min = 14,74-(-15,08) = 29,82

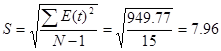
RS =29,82/7.96 = 3.75

Полученое значение RS сравнивают с табличными значениями, которые зависят от количества точек N и уровня значимости. Таблицу значений границ RS-критерия можно найти в литературе [2, стр. 134]. Для N=16 и 5% уровня значимости значение RS для нормального распределения должно находиться в интервале от 3,00 до 4,21

Так как 3,00 < 3,75 < 4,21, полученное значение RS попало в заданный интервал. Значит, уровни ряда остатков подчиняются нормальному распределению.

Таким образом, все условия адекватности и точности выполнены. Следовательно, можно говорить об удовлетворительном качестве модели и возможности проведения прогноза показателя Y_p ( t ) на 4 квартала вперед.