Многократные измерения. Порядок выполнения многократных измерений с равноточными значениями отсчета. Оценка доверительного интервала доверительной вероятности.

При повышенных требованиях к точности измерений для уменьшения погрешности результата измерений проводятся многократные измерения одной и той же величины.

 Однократные измерения повторяются оператором в одинаковых условиях, одними и теми же средствами измерений. Такие измерения применяют при выполнении метрологических работ, а также в научных исследованиях. По результатам многократных измерений проводится анализ, главной особенность которого является получение и использование большего объёма измерительной информации.

Общая последовательность выполнения многократных измерений одной и той же величины сводится к следующему:

- анализу имеющейся информации и подготовки к измерениям;

- получению отсчёта (х₁);

- получению (n) значения показаний (х₁);

     - внесению поправок и получению «n» значений результатов измерений Q_i;

- оценке среднего значения результатов измерений;

- оценке среднеквадратичного отклонения результатов измерения ;

- оценке среднего квадратичного отклонения среднего арифметического значения ;

     - определению пределов, в которых находится значение измеряемой величины .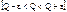

                   Прежде, чем приступить к обобщению результатов измерений, определяют, нет ли в полученных результатах грубых погрешностей.

                   Применение многократных измерений позволяет повысить точность измерения до определённого предела, но не позволяет получить точное значение поправок и значений составляющих погрешностей. В связи с этим, устанавливают необходимое число измерений (не менее 4), в котором случайная погрешность пренебрежно мала по сравнению с исключённой систематической погрешностью.

При интервальной оценке определяется доверительный интервал 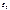, в котором с доверительной вероятностью Р находится истинное значение :

.

При заданной вероятности Р и вычисленной 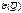 значение tP определяется законом распределения. В случае нормального распределения и числа измерений    выбирается по таблице функций Лапласа, при этом значения вероятности Р умножаются на 2, так как в табл. 2 они приведены для половины симметричного интервала.

Если число измерений , доверительный интервал случайной погрешности при заданных вероятности Р и СКО результата измерения  определяется по формуле Стьюдента: ,

где  – коэффициент распределения Стьюдента, который зависит от заданной вероятности Р и числа измерений n.

При  распределение Стьюдента приближается к нормальному и вместо , можно использовать  для нормального распределения. При равномерном распределении обычно принимают , т.е. для 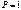, поскольку доверительный интервал слабо зависит от доверительной вероятности. Таким образом, истинное значение, очевидно, будет находиться внутри интервала: .

Можно также выразить относительную случайную погрешность 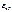, соответствующую доверительной вероятности Р, %, .

Рассмотрим теперь, какую же доверительную вероятность следует брать? Как правило, принимают . Если измерения нельзя повторить, то 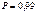, а в особо ответственных случаях, когда проводимые измерения связаны с созданием новых эталонов или имеют значение для здоровья людей, и выше.

В этих случаях при нормальном распределении доверительный интервал , что соответствует доверительной вероятности .