 |
Главная |
Оценивание состояния линеаризованной системы с модальным регулятором при внешних неопределенных ограниченных возмущениях
|
из
5.00
|
Пусть в начальный момент времени  состояние системы является неопределенным, известно, что оно принадлежит эллипсоиду (1.3) где
состояние системы является неопределенным, известно, что оно принадлежит эллипсоиду (1.3) где  – заданная положительно определенная симметрическая матрица.
– заданная положительно определенная симметрическая матрица.
Предполагается, что пара (A,D) –управляема, а матрица C является матрицей полного ранга строк.
Требуется на заданном интервале времени получить эллипсоидальную оценку множества состояний для процессов системы (1.4), начинающихся из заданного эллипсоида 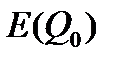 при и неопределенных возмущениях из (1.3) а также установить ограниченность решений исходной системы на конечном интервале относительно заданных множеств.
при и неопределенных возмущениях из (1.3) а также установить ограниченность решений исходной системы на конечном интервале относительно заданных множеств.
Пусть заданы в виде эллипсоидов  ,
,  , (R0, R(t) – известные симметрические положительно определенные матрицы) – соответственно множество начальных отклонений, множество допустимых состояний в моменты времени
, (R0, R(t) – известные симметрические положительно определенные матрицы) – соответственно множество начальных отклонений, множество допустимых состояний в моменты времени 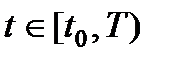 и множество допустимых внешних возмущений W.
и множество допустимых внешних возмущений W.
Определение 1. Будем говорить, что система (1) обладает на  свойством ограниченности относительно заданных множеств [E(R0), E(R(t)), W] (при отсутствии неопределенных внешних возмущений – свойством устойчивости относительно заданных множеств [E(R0), E(R(t))]), если для всех
свойством ограниченности относительно заданных множеств [E(R0), E(R(t)), W] (при отсутствии неопределенных внешних возмущений – свойством устойчивости относительно заданных множеств [E(R0), E(R(t))]), если для всех 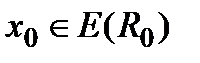 существуют на
существуют на  решения
решения  системы (1) с начальными данными
системы (1) с начальными данными  , для которых имеет место
, для которых имеет место  при всех
при всех  (соответственно
(соответственно  при всех
при всех  .
.
Оценка вектора состояния будет находиться в виде эволюционирующего эллипсоида, инвариантного для процессов системы (1.1).
Напомним, что инвариантным эллипсоидом для динамической системы называется эллипсоид
 , (1.7)
, (1.7)
обладающий следующим свойством: любая траектория системы  , исходящая из точки
, исходящая из точки  , в любой момент времени t принадлежит этому эллипсоиду, т.е.
, в любой момент времени t принадлежит этому эллипсоиду, т.е. 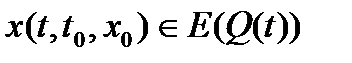 .
.
Инвариантные эллипсоиды характеризуют внешнюю оценку области достижимости в текущий момент времени t при влиянии неопределенных внешних возмущений w(t) на траектории системы (1.4). В этой связи нас будет интересовать минимальные (в некотором смысле) инвариантные эллипсоиды, содержащие траектории или выход z(t) рассматриваемой системы.
Теорема 1.1. Эллипсоид  , где
, где  есть решение матричной системы дифференциальных уравнений
есть решение матричной системы дифференциальных уравнений
 (1.8)
(1.8)
является инвариантным для траекторий системы (1.2), стартующих из начального эллипсоида  , а эллипсоид
, а эллипсоид  является в каждый момент времени ограничивающим для вектора выхода z(t). Если, кроме того, матрица
является в каждый момент времени ограничивающим для вектора выхода z(t). Если, кроме того, матрица 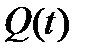 удовлетворяет дополнительно ограничениям
удовлетворяет дополнительно ограничениям  и
и  для всех
для всех 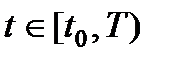 , где R0 и R(t) – заданные положительно определенные симметрические матрицы, то данный регулятор обеспечивает ограниченность замкнутой системы относительно множеств [E(R), Ew(I), E(R(t))] при всех возмущениях из (1.5).
, где R0 и R(t) – заданные положительно определенные симметрические матрицы, то данный регулятор обеспечивает ограниченность замкнутой системы относительно множеств [E(R), Ew(I), E(R(t))] при всех возмущениях из (1.5).
Замечание 1. Матричная система дифференциальных уравнений является системой сравнения (МСС) для линеаризованной системы с неопределенными возмущениями, так как правая часть ее удовлетворяет условию квазимонотонности по Q относительно конуса G+.
Можно показать, что МСС обладает следующими свойствами:
1). Положительность решений – если  (или
(или 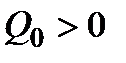 ), то
), то  (соответственно
(соответственно  ) для всех
) для всех  .
.
2) Монотонность решений – для любых  таких, что
таких, что  имеет место
имеет место  для всех
для всех  .
.
3) Инвариантность множества  , где
, где  : множество
: множество  в пространстве матриц G+ положительно инвариантно для решений
в пространстве матриц G+ положительно инвариантно для решений 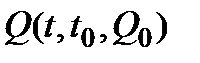 МСС с
МСС с  . Кроме того, найдется
. Кроме того, найдется  такое, что имеет место
такое, что имеет место
 .
.
4) Сходимость решений: если матрица A+BK является гурвицевой, т.е удовлетворяет условию  , где
, где  - собственные значения матрицы замкнутой системы, а параметр q удовлетворяет условию
- собственные значения матрицы замкнутой системы, а параметр q удовлетворяет условию 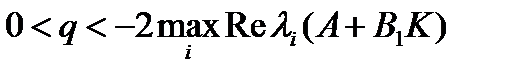 , то существует предел
, то существует предел  , к которому сходятся решения
, к которому сходятся решения  для любых
для любых  . В этом случает матрица
. В этом случает матрица  будет определять предельный инвариантный эллипсоид для решений исходной системы (1.4) с неопределенными возмущениями из (1.5).
будет определять предельный инвариантный эллипсоид для решений исходной системы (1.4) с неопределенными возмущениями из (1.5).
Замечание 2. Указанные свойства имеют место для любой линейной автономной системы с неопределенными ограниченными возмущениями. Они позволяю контролировать процесс получения гарантированных оценок при вычислениях.
Замечание 3. При каждом фиксировано q согласно свойству 4) может быть найдена матрица  предельного инвариантного эллипсоида, который характеризует точность стабилизации рассматриваемой замкнутой системы (1.4) при неопределенных ограниченных возмущений. Для нахождения минимального предельного инвариантного эллипсоида достаточно выполнить численное интегрирование матричной системы сравнения при различных значения параметра q из диапазона
предельного инвариантного эллипсоида, который характеризует точность стабилизации рассматриваемой замкнутой системы (1.4) при неопределенных ограниченных возмущений. Для нахождения минимального предельного инвариантного эллипсоида достаточно выполнить численное интегрирование матричной системы сравнения при различных значения параметра q из диапазона 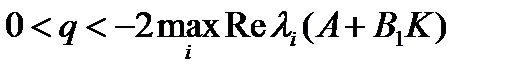 , и выбрать то значение q, при котором достигается
, и выбрать то значение q, при котором достигается  (минимум следа матрицы
(минимум следа матрицы  ).
).
Задача нахождения минимального предельного инвариантного эллипсоида может быть сведена к задаче оптимизации с линейными матричными неравенствами.
Теорема 1.2. Решение  задачи
задачи

при ограничениях Q>0,
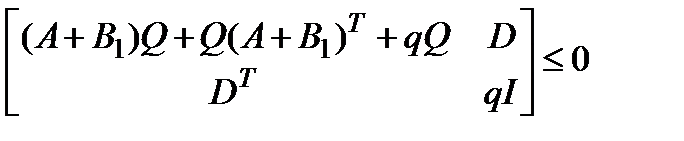 (1.9)
(1.9)
где минимизация проводится по матричной переменной 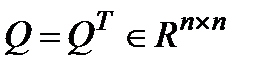 и скалярной параметру q>0, определяет матрицу
и скалярной параметру q>0, определяет матрицу 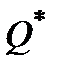 ограничивающего эллипсоида для вектора состояния x(t), и матрицу
ограничивающего эллипсоида для вектора состояния x(t), и матрицу  ограничивающего эллипсоида для вектора выхода z(t) системы (1.4).
ограничивающего эллипсоида для вектора выхода z(t) системы (1.4).
Доказательство проводится с использованием свойств 3),4) МСС (1.8). При этом условие  из свойства 4) представляется эквивалентным по лемме дополнения Шура условием (1.9).
из свойства 4) представляется эквивалентным по лемме дополнения Шура условием (1.9).
Далее приводится фрагмент текста программы для решения задачи оптимизации (с помощью программного обеспечения CVX решения линейных матричных неравенств) и нахождения минимального инвариантного эллипсоида путем перебора параметра q из заданного диапазона.
%-----модель математического маятника -------
% Примеры синтеза оценивания состояния и моделирования
%--Исходные данные --Линеаризованная модель с неопределенными возмущениями
% вектор состояния x=(x1,x2)T
n=2;
m=1;
l=1;
n1=n;
w=0.5;
mu1=1;
A = [0 1; -w*w 0];
B1 = [0; 1];
D=[0; 1];
C=[1 0;0 1;0 0];
B2=[0; 0;1];
eig(A)
p=[-1. -3];
K0=-place(A,B1,p);
ABK0=A+B1*K0;
% Нахождение предельного инвариантного эллипсоида замкнутой системы с
% матрицей A+B*K0 и оптимизацией по параметру q;
A0=ABK0;
min_tr_Q=1e+4;
for q = 0.1:0.002:1;% 0.944:0.002:0.944
cvx_begin sdp
variable Qs(n, n) symmetric;
minimize( trace(Qs))
subject to
Qs >= eye(2)*10e-5;
[A0*Qs + Qs*A0'+q*Qs D;
D' -q*eye(l)]< 0; %условие асимптотич устойчивости
cvx_end
Qsf = double(Qs)
trQ=trace(Qsf);
if min_tr_Q > trQ
min_tr_Q = trQ;
Q_min = Qsf;
q_min = q
end;
end;
Q0 = Q_min;
q0=q_min;
С помощью данной программы в пакете Matlab была получена матрица минимального предельного инвариантного эллипсоида

при  , q*=0.944 для системы (1.4).
, q*=0.944 для системы (1.4).
Построение оценок состояния линеаризованной системы с неопределенными ограниченными возмущениями производилось на основе теоремы 1.1. Для численного интегрирования МСС (1.8) на заданном интервале [t0,tk] использовалась стандартная функция пакета Matlab ode15s, вызов которой показан в следующем фрагменте программы.
% Оценивание состояния маятника с неопределенными возмущениями с помощью
% матричной системы сравнения
t0=0; tk=10;
Q=eye(1.2)*2;
vec_Q = [Q(:,1); Q(:,2)];
[t,H] =ode15s(@(t,vec_Q) Prav_Lin_Mayat_1(t,vec_Q,A0,D,q0),[t0 tk],vec_Q);
MQ = [];
nh=length(H(:,1));
t(nh)
nn=1;%round(nh/20);
figure(1)
for i = 1:nn:nh
MQ = [H(i,1) H(i,2); H(i,3) H(i,4)];
MQ=(MQ+MQ')/2;
E = ellipsoid(MQ);
%pEs = projection(E, BB);
plot(E, 'b');grid on;hold on;
end;
plot(E, 'r');grid on;hold on;
Здесь функция Prav_Lin_Mayat_1 служит для вычисления правой части МСС (1.9).
function dQ=Prav_Lin_Mayat_1(t,vec_Q,A,D,q)
% Вычисление правой части матричной системы сравнения и определение матрицы
% коэффициентов усиления регулятора в текущий момент времени
Q = [ vec_Q(1) vec_Q(2); vec_Q(3) vec_Q(4)];
dQQ= A*Q + Q*A' +q*Q+(D*D')/q;
dQQ=(dQQ+dQQ')/2;
dQ = reshape(dQQ,4,1);
На рисунке 1.1 показаны сечения эволюционирующего инвариантного эллипса, полученные на основе численного решения МСС с начальной матрицей
 ,
,
определяющей начальный эллипсоид  (показан штриховой линией). Решение сошлось за T<10c к предельному инвариантному эллипсу с матрицей MQ*
(показан штриховой линией). Решение сошлось за T<10c к предельному инвариантному эллипсу с матрицей MQ*
 ,
,
которая практически совпадает с матрицей  минимального предельного инвариантного эллипса.
минимального предельного инвариантного эллипса.
Рисунок 1.1. Эволюционирующий инвариантный эллипс для решений линеаризованной системы с модальным регулятором.
|
из
5.00
|
Обсуждение в статье: Оценивание состояния линеаризованной системы с модальным регулятором при внешних неопределенных ограниченных возмущениях |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

