 |
Главная |
Метод векторных контуров в кинематике механизмов
|
из
5.00
|
Кинематическому анализу механизма предшествует задача структурного анализа. Результатом структурного анализа является символическая формула строения механизма (формула (1.5) для механизма Рис.1). Эта же формула, как правило, определяет последовательность формирования алгоритма кинематического анализа, т.е. является алгоритмической формулой. Смысл ее в следующем: как механизм на стойке собирается путем последовательного присоединения кинематических групп, так и алгоритм кинематического анализа формируется последовательным соединением расчетных модулей, каждый из которых позволяет выполнить кинематическое исследование соответствующей группы. При этом результаты исследования одной группы становятся исходными данными для анализа следующих.
Исследование плоских рычажных механизмов удобно проводить методом векторных контуров, разработанным проф. В.А.Зиновьевым. В этом методе связи в механизме, определяемые как видом кинематических пар, так и размерами звеньев, выражаются в форме условий замкнутости векторных контуров, построенных на базе кинематической схемы механизма. В скалярной форме соответствующие зависимости получают, проецируя контуры на оси координат.
В ДЗ анализируется плоский рычажный механизм, в состав которого входят двухзвенные группы с нулевой подвижностью (группы Ассура) и (или) группы со степенью подвижности 1. Векторные контуры составляют для каждой входящей в механизм группы Ассура. Построенные на базе векторных контуров расчетные модули объединяют в единый расчетный алгоритм согласно алгоритмической формуле, полученной при решении задачи структурного анализа механизма.
Сформулируем формальные правила, которые в дальнейшем будем соблюдать:
- выберем правую декартову систему координат 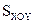 , начало которой
, начало которой  совпадает с неподвижной точкой начального звена;
совпадает с неподвижной точкой начального звена;
- правило отсчета углов: угол  будем отсчитывать от положительного направления оси
будем отсчитывать от положительного направления оси 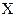 до положительного направления соответствующего вектора, двигаясь против хода часовой стрелки.
до положительного направления соответствующего вектора, двигаясь против хода часовой стрелки.
Получим функции положения для условного механизма 1-го класса IВ(0,1) и групп Ассура 2-го класса (диад). Аргумент функций – обобщенная координата  (в дальнейшем подразумевается, но не пишется).
(в дальнейшем подразумевается, но не пишется).
2.2.1 Анализ группы IВ(0,1)
Воспользуемся Рис. 2.
Дано:  ;
;  ;
;  ;
;  - угол, соответствующий начальному положению входного звена.
- угол, соответствующий начальному положению входного звена.
Найти: функцию положения точки  :
: 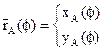
Функция 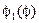 учитывает заданное направление вращения звена 1 в составе механизма:
учитывает заданное направление вращения звена 1 в составе механизма: 
Запишем: 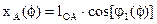 ;
; 
Фрагмент записи в системе Mathcad


Построим расчетные модули кинематического анализа для групп Ассура 2-го класса.
2.2.2. Группа IIВВВ(2,3)
 Дано:
Дано: 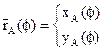 ,
, 
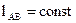 ;
; 
Найти: функции положения 2-го и 3-го звена: 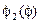 и
и 
Запишем условие замкнутости векторного контура

В проекциях на оси координат
(Здесь, и в дальнейшем, при выводе расчетных формул аргумент  будем опускать):Рис. 3.
будем опускать):Рис. 3. 
Решение полученной системы трансцендентных уравнений можно получить только приближенными, итерационными методами. В системе Mathcad решение может быть найдено с использованием процедуры Given- Find, что требует необходимости задания начальных приближений неизвестным 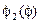 и
и  . Начальные приближения задаются на основании построенного при любом значении
. Начальные приближения задаются на основании построенного при любом значении  плана механизма.
плана механизма.
Фрагмент записи в системе Mathcad

Функция  - возвращает значение одной или ряда переменных для точного решения системы уравнений в блоке, объявленном директивой
- возвращает значение одной или ряда переменных для точного решения системы уравнений в блоке, объявленном директивой  , который кроме решаемой системы уравнений может содержать и условия ограничения. Вместо функции
, который кроме решаемой системы уравнений может содержать и условия ограничения. Вместо функции  может
может
использоваться, например, функция  , которая возвращает значение одной или нескольким переменным для приближенного решения системы нелинейных уравнений.
, которая возвращает значение одной или нескольким переменным для приближенного решения системы нелинейных уравнений.
2.2.3. Группа IIВВП(2,3)
 Дано:
Дано: 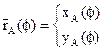 ,
, 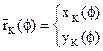
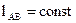 ; угловое положение
; угловое положение 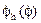
направляющей для ползуна 3.
Найти: функцию положения 2-го звена 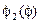 и функцию перемещения
и функцию перемещения  ползуна 3.
ползуна 3.
Запишем условие замкнутости векторного контура

В проекциях на оси координат
Рис. 4.  ,
,
 . В системе Mathcad искомые функции
. В системе Mathcad искомые функции 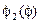 и
и  могут быть найдены несколькими способами.
могут быть найдены несколькими способами.
1. Решим исходную систему двух уравнений с использованием функции  в блоке
в блоке  , что требует необходимости задания начальных приближений неизвестным
, что требует необходимости задания начальных приближений неизвестным 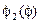 и
и  .
.
Фрагмент записи расчетного модуля в системе Mathcad

2. Решим исходную систему уравнений относительно 3-х переменных:  ,
, 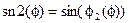 и
и  , что потребует задания еще одного уравнения:
, что потребует задания еще одного уравнения:  .
.
Фрагмент записи расчетного модуля в системе Mathcad

Функция 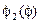 найдена с использованием стандартной функции
найдена с использованием стандартной функции  . Функция позволяет найти угол между осью
. Функция позволяет найти угол между осью 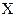 и отрезком прямой с конечными точками
и отрезком прямой с конечными точками  и
и  , причем
, причем  и
и  должны быть реальными значениями.
должны быть реальными значениями.
3. Возведем каждое из уравнений исходной системы в квадрат и сложим. Получим квадратное уравнение относительно 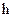 :
:
 ,
,
где  ,
,  .
.
Для решения полученного уравнения вместо функции  будем использовать функцию
будем использовать функцию  . Далее, из первого уравнения системы найдем
. Далее, из первого уравнения системы найдем  , из второго
, из второго  .
.
Фрагмент записи расчетного модуля в системе Mathcad
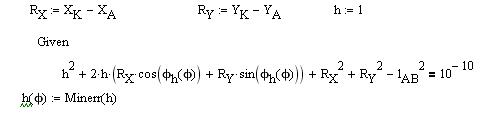


4. (Способ предложен В.В.Кузенковым). Неизвестную функцию 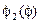 будем искать в виде
будем искать в виде  . Тогда исходная система уравнений примет вид
. Тогда исходная система уравнений примет вид
 ,
,

Фрагмент записи расчетного модуля в системе Mathcad

Группа IIВВП(2,3) с горизонтальным перемещением ползуна
 Дано:
Дано: 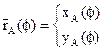 ;
; 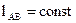 ;
;  ;
;
Найти: функцию положения 2-го звена 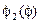 и функцию перемещения
и функцию перемещения  ползуна 3.
ползуна 3.
Условие замкнутости векторного контура 
В проекциях на оси координат
Рис. 5. 
Получим расчетные формулы для неизвестных 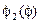 и
и  . Из второго уравнения системы найдем
. Из второго уравнения системы найдем 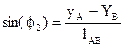 . Затем
. Затем 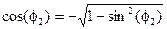 (знак минус перед радикалом соответствует правой сборке группы Ассура, угол
(знак минус перед радикалом соответствует правой сборке группы Ассура, угол  изменяется в пределах
изменяется в пределах  <
<  <
<  ). Функция
). Функция 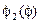 в системе Mathcad может быть найдена с помощью стандартной функции
в системе Mathcad может быть найдена с помощью стандартной функции  . Из первого уравнения системы найдем выражение для
. Из первого уравнения системы найдем выражение для  :
: 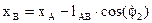 .
.
Фрагмент записи расчетного модуля в системе Mathcad

2.2.5. Группа IIВВП(2,3) с вертикальным перемещением ползуна
 Дано:
Дано: 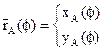 ;
; 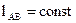 ;
;
 ;
;
Найти: функцию положения 2-го звена 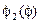 и функцию перемещения
и функцию перемещения  ползуна 3.
ползуна 3.
Условие замкнутости векторного контура 
В проекциях на оси координат
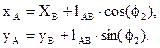
Рис. 6.
Получим расчетные формулы для неизвестных 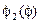 и
и  . Из первого уравнения системы найдем
. Из первого уравнения системы найдем  . Затем
. Затем  (знак плюс перед радикалом соответствует нижней сборке группы Ассура, угол
(знак плюс перед радикалом соответствует нижней сборке группы Ассура, угол  изменяется в пределах 0 <
изменяется в пределах 0 <  <
<  ). Функция
). Функция 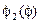 в системе Mathcad может быть найдена с помощью стандартной функции
в системе Mathcad может быть найдена с помощью стандартной функции  . Из второго уравнения системы получим выражение
. Из второго уравнения системы получим выражение  :
:  .
.
Фрагмент записи расчетного модуля в системе Mathcad


2.2.6. Группа IIВПВ(2,3)
Дано: 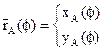 ;
;  ;
;
Найти: функцию положения 3-го звена 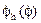 и функцию относительного перемещения
и функцию относительного перемещения  ползуна 2.
ползуна 2.
Условие замкнутости векторного контура 
В проекциях на оси координат

Рис. 7.
Возведем уравнения системы в квадрат и сложим их. Из полученного выражения найдем  . Затем, из первого уравнения получим
. Затем, из первого уравнения получим  , из второго уравнения
, из второго уравнения  .
.
Функция 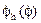 в системе Mathcad может быть найдена с помощью стандартной функции
в системе Mathcad может быть найдена с помощью стандартной функции  .
.
Фрагмент записи расчетного модуля в системе Mathcad 
 2.2.7. Группа IIВПВ(2,3) с эксцентриситетом
2.2.7. Группа IIВПВ(2,3) с эксцентриситетом
Дано: 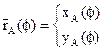 ;
;  ;
;
величина эксцентриситета  .
.
Найти: функцию положения 3-го звена 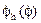 и функцию относительного перемещения
и функцию относительного перемещения  ползуна 2
ползуна 2
Условие замкнутости векторного контура 
В проекциях на оси координат
Рис. 8. 
После приведения

В системе Mathcad искомые функции 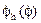 и
и  могут быть найдены с использованием процедуры Given - Find, что требует необходимости задания начальных приближений неизвестным
могут быть найдены с использованием процедуры Given - Find, что требует необходимости задания начальных приближений неизвестным 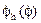 и
и  .
.
Фрагмент записи расчетного модуля в системе Mathcad

2.2.8. Группа IIПВП(2,3) общего вида
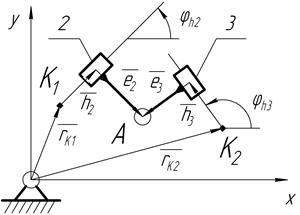 Дано:
Дано:  ;
; 
величина эксцентриситета:  - для ползуна 2,
- для ползуна 2,  - для ползуна 3;
- для ползуна 3;
угловое положение направляющих
 ,
,  .
.
Найти: функции относительного
перемещения:  ползуна 2,
ползуна 2,
 ползуна 3.
ползуна 3.
Условие замкнутости векторного контура
Рис. 9. 
В проекциях на оси координат
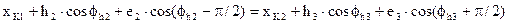 ,
,
 .
.
После приведения
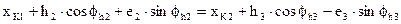 ,
,
 .
.
В системе Mathcad искомые функции 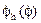 и
и  могут быть найдены с использованием процедуры Given - Find, что требует необходимости задания начальных приближений неизвестным
могут быть найдены с использованием процедуры Given - Find, что требует необходимости задания начальных приближений неизвестным 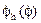 и
и  .
.
Фрагмент записи расчетного модуля в системе Mathcad
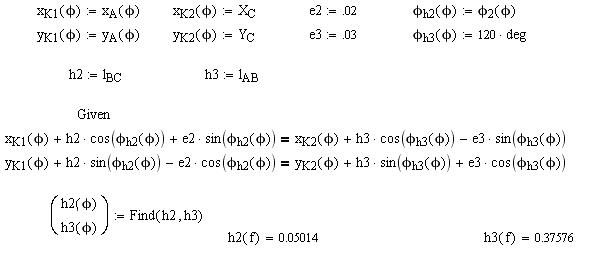
2.2.9. Группа IIПВП(2,3) с вертикальным перемещением ползуна
 Дано:
Дано: 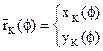 ; координата
; координата  направляющей ползуна 3;
направляющей ползуна 3;
угловое положение направляющей
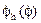 ползуна 2.
ползуна 2.
Найти: функцию относительного перемещения  ползуна 2,
ползуна 2,
функцию перемещения  ползуна 3.
ползуна 3.
Условие замкнутости векторного контура: 
В проекциях на оси координат Рис. 10. 
Из первого уравнения найдем  , подставим полученное выражение во второе уравнение. Найдем
, подставим полученное выражение во второе уравнение. Найдем 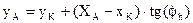 .
.
Фрагмент записи расчетного модуля в системе Mathcad 
2.2.10. Группа IIПВП(2,3) с горизонтальным перемещением ползуна
 Дано:
Дано: 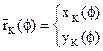 ; координата
; координата
 направляющей ползуна 3;
направляющей ползуна 3;
угловое положение направляющей
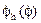 ползуна 2.
ползуна 2.
Найти: функцию относительного перемещения  ползуна 2,
ползуна 2,
функцию перемещения  ползуна 3.
ползуна 3.
Условие замкнутости векторного контура: 
В проекциях на оси координат
Рис. 11. 
Из второго уравнения найдем 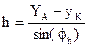 , подставим полученное выражение в первое уравнение. Найдем
, подставим полученное выражение в первое уравнение. Найдем  .
.
Фрагмент записи расчетного модуля в системе Mathcad 
2.2.11.  Группа IIВПП(2,3)
Группа IIВПП(2,3)
Дано: 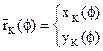 ;
; 
угловое положение  вектора
вектора  Найти:
Найти: 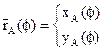
Условие замкнутости векторного контура:

В проекциях на оси координат Рис.12. 
Фрагмент записи расчетного модуля в системе Mathcad

2.2.12. Вспомогательный контур
Предназначен для расчета кинематических параметров присоединительных пар и характерных точек.
 Дано:
Дано:  ;
; 
угловое положение  вектора
вектора  Найти:
Найти: 
В проекциях на оси системы координат
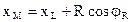 ,
,
Рис. 13.  .
.
|
из
5.00
|
Обсуждение в статье: Метод векторных контуров в кинематике механизмов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

