Проблема идентификации системы одновременных уравнений СОУ

Запишем структурную форму эконометрической модели в матричном виде:

, (1.1), где – вектор-столбец значений эндогенных переменных, определяемых внутри модели (m – число эндогенных переменных в системе);

– вектор-столбец значений предопределенных переменных, которые могут включать как экзогенные переменных (внешние по отношению к системе), так и лаговые значение эндогенных переменных (k – число предопределенных переменных в системе);

- вектор-столбец случайных возмущений; t – номер (момент) наблюдения;

· Матрица коэффициентов перед вектором эндогенных переменных модели;

- Матрица коэффициентов перед вектором предопределенных переменных модели. Одно из основных требований к предопределенным переменным – некоррелированность со случайными возмущениями в каждом наблюдении t.
Предполагая что матрица А невырождена, умножив обе части равенства (1.1) на , получим приведенную форму модели:

, (1.2), где 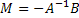(1.3) – матрица коэффициентов приведенной формы, (1.4) – вектор случайных возмущений приведенной формы.

Как следует из (1.3), структурные коэффициенты А и В связаны с приведенными коэффициентами модели соотношением: (1.5).

В общем случае, как было показано выше, эндогенные переменные одного уравнения структурной формы могут быть регрессорами в других уравнениях, что приводит к их коррелированности со случайными возмущениями, поэтому применение к какому-либо из уравнений МНК дает смещенные и несостоятельные оценки. Коэффициенты приведенной формы могут быть состоятельно оценены МНК, поскольку регрессоры приведенной формы некоррелированы со структурными возмущениями и следовательно (см.(1.4)), с приведенными возмущениями . Т.о., задача состоит в оценке структурных коэффициентов по приведенным. Рассчитаем количество исходных данных, которые могут быть использованы при определении структурных параметров:

· mk – элементов матрицы М приведенных коэффициентов;

· – элементов атоковариационной матрицы вектора возмущений .

В структурной форме неизвестными являются:

· – число элементов матрицы А (с учетом нормализации);

· mk – элементов матрицы В;

· – элементов атоковариационной матрицы вектора возмущений .

Т.о., неизвестных структурных коэффициентов больше, чем оцененных приведенных на величину , и, следовательно, в общем случае система одновременных уравнений неидентифицируема.

Однако при наличии априорных ограничений на структурные коэффициенты некоторые структурные уравнения могут быть идентифицированы, поэтому в дальнейшем будет рассматриваться задача идентификации отдельного уравнения. В качестве ограничений на структурные коэффициенты обычно используются следующие простейшие:

· Часть структурных коэффициентов равна нулю, т.е. между экономическими переменными, входящими в систему, в данном уравнении нет связи;

· Часть структурных коэффициентов равна единице (в случае тождества, или условия нормализации).

Если таких ограничений недостаточно для однозначного определения структурных коэффициентов через приведенные, то говорят, что уравнение неидентифицируемо.