 |
Главная |
Теорема (существование и вычисление обратной матрицы)
|
из
5.00
|
А) Матрица  обратима
обратима 
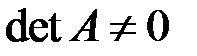 .
.
Б) Обратную матрицу можно вычислить по формуле
 . (2.3)
. (2.3)
Свойства обратной матрицы:
1)  ,
,
2) 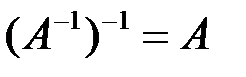 ,
,
3) если  и
и  обратимые матрицы одного порядка, то матрица
обратимые матрицы одного порядка, то матрица  обратима и
обратима и 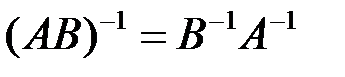 ,
,
4)  ,
,
5)  =
=  .
.
Примеры решения задач
2.2.1.Найти матрицу  , если
, если  ,
,  .
.
◄ 1) Произведение матрицы  на число 2 – матрица
на число 2 – матрица
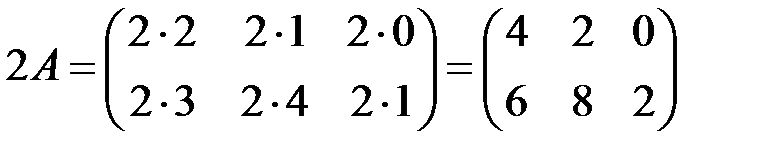 .
.
2) Поместив каждую строку матрицы  на место столбца с тем же номером, получим транспонированную матрицу
на место столбца с тем же номером, получим транспонированную матрицу  .
.
3) Так как размеры матриц 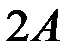 и
и  одинаковые –
одинаковые –  – то определена сумма этих матриц – матрица
– то определена сумма этих матриц – матрица
 . ►
. ►
2.2.2.Для матриц 
 и
и  найти следующие произведения:
найти следующие произведения: 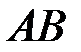 и
и 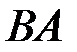 ,
,  ,
,  и
и  .
.
◄ 1) Так как (длина строк  )
)  (высота столбцов
(высота столбцов  )
)  , то произведение
, то произведение 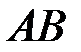 определено. Матрица
определено. Матрица 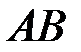 имеет столько же строк – 2, что и первый сомножитель
имеет столько же строк – 2, что и первый сомножитель  , и столько же столбцов – 2, что и второй сомножитель
, и столько же столбцов – 2, что и второй сомножитель  . Находим
. Находим 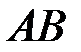 по правилу (2.1) – «строка первого сомножителя на столбец второго»:
по правилу (2.1) – «строка первого сомножителя на столбец второго»:
 .
.
2) Так как (длина строк  )
)  (высота столбцов
(высота столбцов  )
)  , то произведение
, то произведение  также определено:
также определено:
 .
.
Мы видим, что  , то есть произведение зависит от порядка сомножителей.
, то есть произведение зависит от порядка сомножителей.
3) 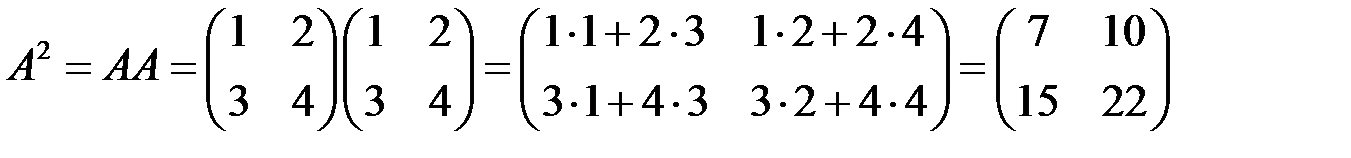 .
.
4) Так как (длина строк  )
)  (высота столбцов
(высота столбцов 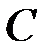 )
)  , то матрица
, то матрица  определена и имеет столько же строк – 3, что и первый сомножитель
определена и имеет столько же строк – 3, что и первый сомножитель  , и столько же столбцов – 3, что и второй сомножитель
, и столько же столбцов – 3, что и второй сомножитель 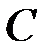 :
:
 .
.
Так как (длина строк 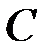 )
)  (высота столбцов
(высота столбцов  )
)  , то матрица
, то матрица  определена и имеет столько же строк – 2, что и первый сомножитель
определена и имеет столько же строк – 2, что и первый сомножитель 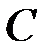 , и столько же столбцов – 2, что и второй сомножитель
, и столько же столбцов – 2, что и второй сомножитель  :
:
 .►
.►
2.2.3.Пусть  –
–  -матрица,
-матрица,  –
–  -матрица,
-матрица,  –
– 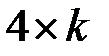 -матрица. Если а)
-матрица. Если а)  или б)
или б)  , то какими могут быть значения
, то какими могут быть значения  и
и  ?
?
◄) а) Если  , то
, то
(длина строк  )
) 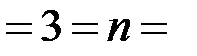 (высота столбцов
(высота столбцов  ),
),
(число строк  )
) 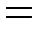 (число строк
(число строк  )
) 
 (число строк
(число строк  ),
),
(число столбцов  )
) 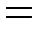 (число столбцов
(число столбцов  )
) 
 (число столбцов
(число столбцов  ).
).
Таким образом,  и
и  .
.
б) Если  , то
, то  –
–  -матрица,
-матрица,
(длина строк  )
)  (высота столбцов
(высота столбцов 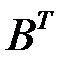 ),
),
(число строк 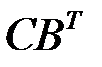 )
) 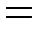 (число строк
(число строк  )
) 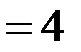
 (число строк
(число строк  ),
),
(число столбцов 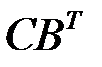 )
)  (число столбцов
(число столбцов  )
) 
 (число столбцов
(число столбцов  ).
).
Таким образом,  и
и  . ►
. ►
2.2.4.Проверить, что матрица  обратима, найти обратную матрицу
обратима, найти обратную матрицу 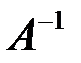 по формуле (2.3), сделать проверку, пользуясь определением обратной матрицы.
по формуле (2.3), сделать проверку, пользуясь определением обратной матрицы.
◄ Матрица  – квадратная, ее определитель
– квадратная, ее определитель
 ,
,
следовательно, матрица обратима, то есть обратная матрица 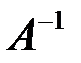 существует. Найдем ее по формуле (2.3). Сначала найдем алгебраические дополнения
существует. Найдем ее по формуле (2.3). Сначала найдем алгебраические дополнения  элементов матрицы
элементов матрицы  :
:
 ,
,  ,
,
 ,
,  .
.
Теперь
 .
.
Сделаем проверку
 ,
,
то есть  . Аналогично проверяется (проверьте!), что
. Аналогично проверяется (проверьте!), что  .
.
Согласно определению (формула (2.2)) найденная матрица является обратной к  .►
.►
2.2.5.Проверить, что матрица  обратима, и найти для нее обратную матрицу.
обратима, и найти для нее обратную матрицу.
◄ Найдем определитель матрицы:


Так как  , то матрица обратима. Найдем обратную матрицу
, то матрица обратима. Найдем обратную матрицу 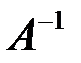 по формуле (2.3). Сначала выпишем и вычислим алгебраические дополнения
по формуле (2.3). Сначала выпишем и вычислим алгебраические дополнения  элементов матрицы
элементов матрицы  :
:
 ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
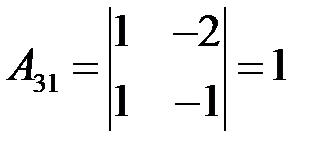 ,
,  ,
,  .
.
По формуле (2.3) получаем

и, окончательно,  . ►
. ►
2.2.6.Найти 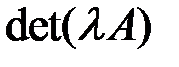 и
и  , если
, если  – квадратная матрица
– квадратная матрица 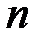 -го порядка с
-го порядка с  .
.
◄ Матрица  получается из матрицы
получается из матрицы  умножением каждой строки на число
умножением каждой строки на число  . По свойству однородности определителя общий множитель каждой из
. По свойству однородности определителя общий множитель каждой из 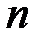 строк можно вынести за знак определителя:
строк можно вынести за знак определителя:
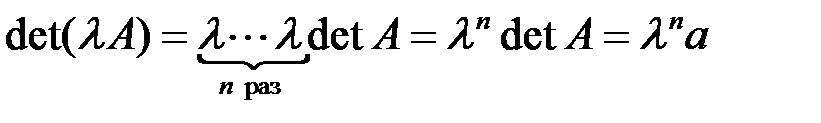 .
.
В силу свойства 1) умножения матриц в произведении  можно не ставить скобки:
можно не ставить скобки:  . По свойству 5) произведения
. По свойству 5) произведения  . Используя свойство 1) обратной матрицы и свойство 5) операции транспонирования, получаем
. Используя свойство 1) обратной матрицы и свойство 5) операции транспонирования, получаем  .►
.►
2.2.7.Упростить выражение 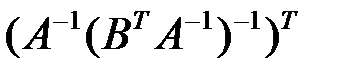 , где
, где 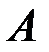 и
и  – квадратные матрицы одного порядка.
– квадратные матрицы одного порядка.
◄ Используем свойства 2)-4) обратной матрицы, формулу (2.2), свойства операций умножения и транспонирования:

 .►
.►
|
из
5.00
|
Обсуждение в статье: Теорема (существование и вычисление обратной матрицы) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

