 |
Главная |
Задачи для самостоятельного решения. В задачах 2.3.3-2.3.4 найти и . 2.3.3
|
из
5.00
|
В задачах 2.1.1-2.1.2. найти матрицы 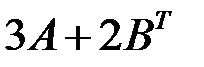 и
и 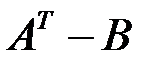 .
.
2.3.1. 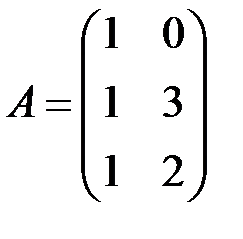 , , 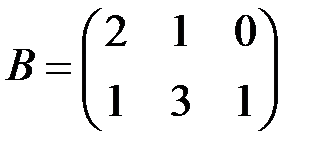 . .
| 2.3.2. 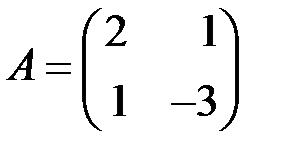 , , 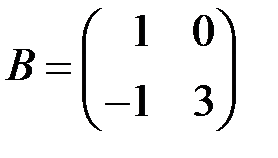 . .
|
В задачах 2.3.3-2.3.4 найти 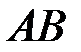 и
и 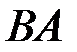 .
.
2.3.3. 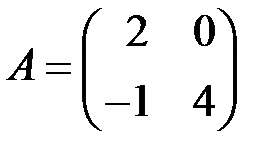 , , 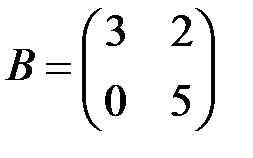 . .
| 2.3.4. 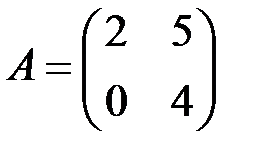 , , 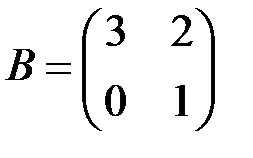 . .
|
В задачах 2.3.5-2.3.6 найти 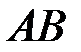 и
и 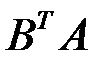 .
.
2.3.5. 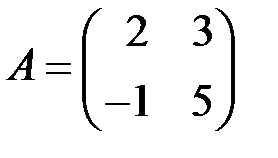 , , 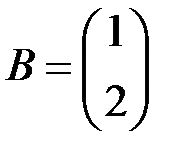 . .
| 2.3.6. 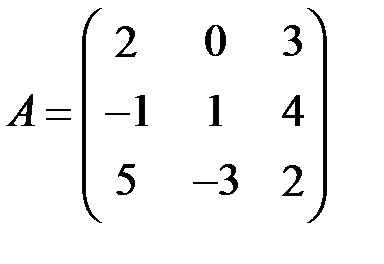 , , 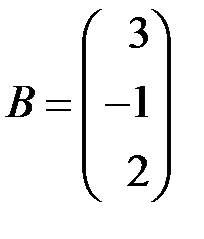 . .
|
2.3.7.Найти 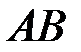 и
и 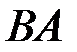 , если
, если 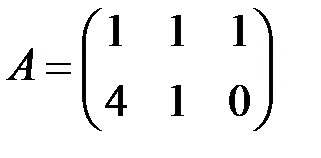 ,
, 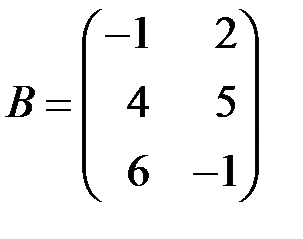 .
.
2.3.8.Найти 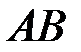 , если
, если  ,
, 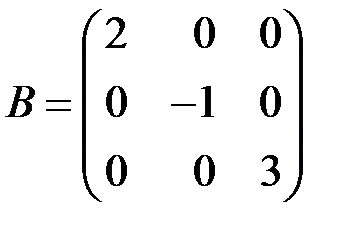 .
.
2.3.9.Для матрицы 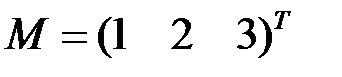 найти
найти 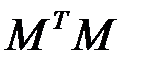 и
и 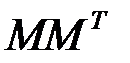 .
.
2.3.10.Для матрицы 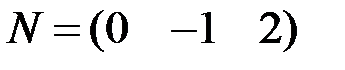 найти
найти 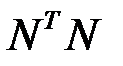 и
и 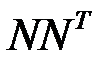 .
.
2.3.11.Для матриц 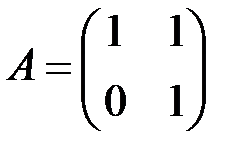 и
и 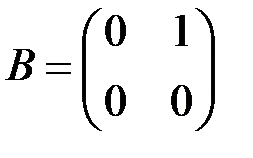 найти
найти 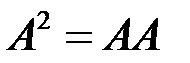 ,
, 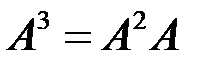 , …,
, …, 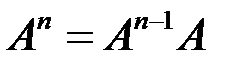 и
и 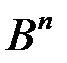 ,
, 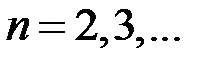
2.3.12.Для матрицы 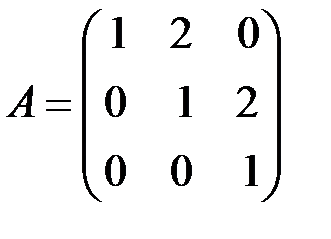 найти
найти 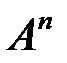 ,
, 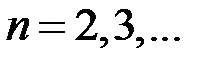
2.3.13.Известно, что  , где
, где  –
– 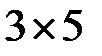 -матрица, а
-матрица, а  –
– 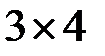 -матрица. Найти размеры матрицы
-матрица. Найти размеры матрицы  .
.
2.3.14.Известно, что  , где
, где 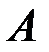 –
–  -матрица, а
-матрица, а  –
– 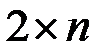 -матрица, а
-матрица, а 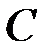 –
– 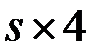 -матрица. Найти
-матрица. Найти  ,
,  и
и 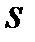 .
.
2.3.15.Пусть 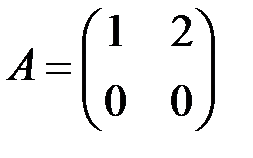 ,
, 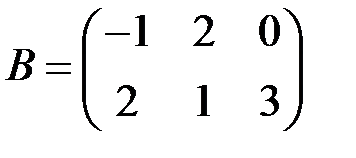 и
и 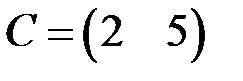 . Существуют ли следующие произведения:
. Существуют ли следующие произведения:
a) 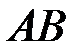 , ,
| b) 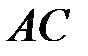 , ,
| c)  , ,
| d) 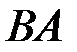 , ,
| e) 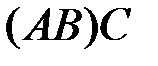 , ,
| f) 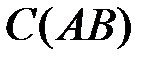 . .
|
2.3.16.Даны матрицы 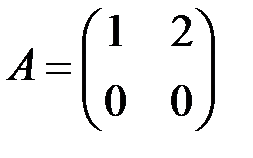 ,
, 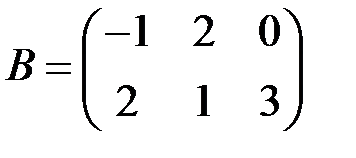 и
и 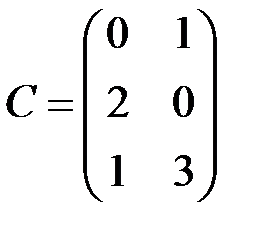 и
и 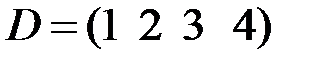 . Существуют ли следующие произведения:
. Существуют ли следующие произведения:
a) 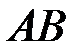 , ,
| b) 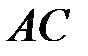 , ,
| c) 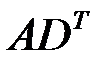 , ,
|
d) 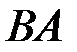 , ,
| e) 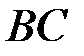 , ,
| f) 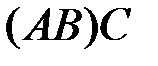 , ,
|
g) 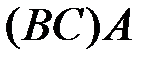
| h) 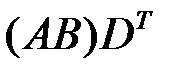 , ,
| i) 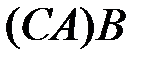 . .
|
В задачах 2.3.17-2.3.18 для матрицы  найти обратную матрицу
найти обратную матрицу  .
.
2.3.17. 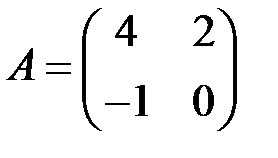 . .
| 2.3.18. 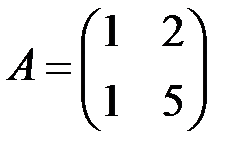 . .
|
В задачах 2.3.19-2.2.20 выяснить является ли матрица 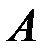 обратимой.
обратимой.
2.3.19. 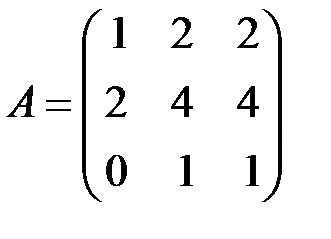 . .
| 2.3.20. 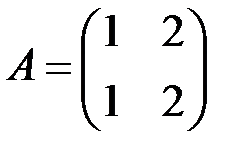 . .
|
В задачах 2.3.21-2.2.22 найти матрицу, обратную к заданной.
2.3.21. 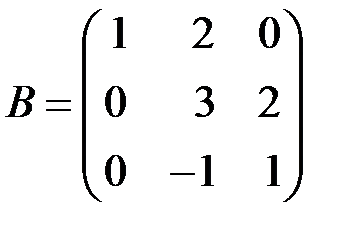 . .
| 2.3.22. 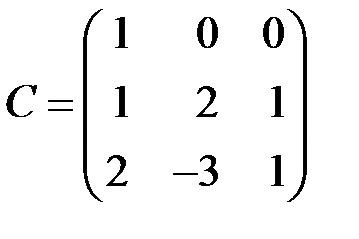 . .
|
2.3.23.Решить матричное уравнение 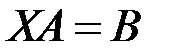 , где
, где 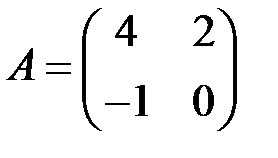 ,
, 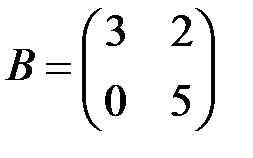 .
.
2.3.24.Решить матричное уравнение 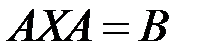 , где
, где 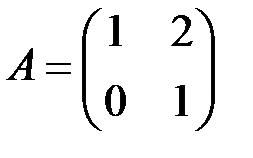 ,
, 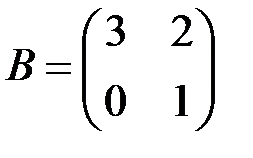 .
.
2.3.25.Упростить выражение 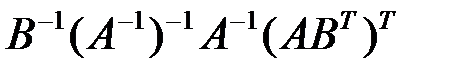 , где
, где 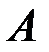 и
и  – квадратные матрицы одного порядка.
– квадратные матрицы одного порядка.
2.3.26.Пусть 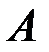 – квадратная матрица с ненулевым определителем.
– квадратная матрица с ненулевым определителем.
1) Упростить выражение для матрицы 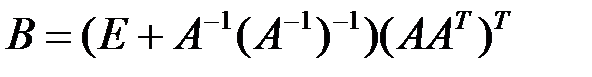 ;
;
2) доказать, что 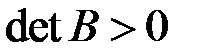 .
.
2.3.27.Пусть 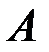 – квадратная матрица второго порядка с ненулевым определителем. Найти
– квадратная матрица второго порядка с ненулевым определителем. Найти 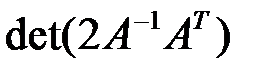 .
.
2.3.28.Пусть 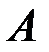 – квадратная матрица третьего порядка с
– квадратная матрица третьего порядка с 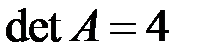 . Найти
. Найти 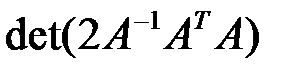 .
.
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Основные понятия и формулы
Система линейных уравнений и ее матричная запись
Система 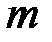 линейных уравнений с
линейных уравнений с 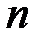 неизвестными
неизвестными 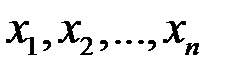 (или просто линейная система) имеет вид
(или просто линейная система) имеет вид
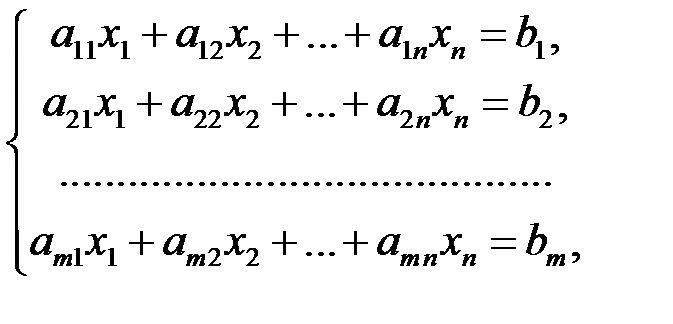 (3.1)
(3.1)
где  – коэффициенты системы и
– коэффициенты системы и 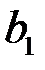 ,
, 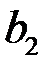 ,…,
,…, 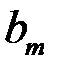 – свободные члены – заданные числа.
– свободные члены – заданные числа.
Введем основную матрицу системы, матрицу-столбец неизвестных и матрицу-столбец свободных членов:
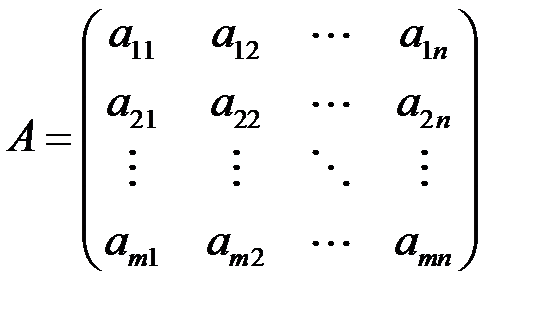 ,
,  и
и  .
.
В этих обозначениях линейную систему (3.1) можно записать в виде одного матричного уравнения
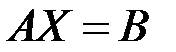 . (
. ( 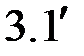 )
)
Решением линейной системы (3.1) называется любой упорядоченный набор чисел – матрица-столбец 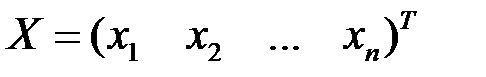 , при подстановке которых в систему на место неизвестных получаем верные равенства.
, при подстановке которых в систему на место неизвестных получаем верные равенства.
Линейная система может быть несовместна – не иметь решений, совместна – иметь хотя бы одно решение. Совместная система может быть определенной – иметь единственное решение и неопределенной – иметь более одного решения.
Невырожденные квадратные линейные системы.
Матричное решение. Формулы Крамера
Линейную систему (3.1) с числом уравнений 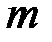 равным числу неизвестных
равным числу неизвестных 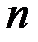 будем называть квадратной, поскольку квадратной является основная матрица
будем называть квадратной, поскольку квадратной является основная матрица 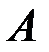 системы, и невырожденной, если
системы, и невырожденной, если  , то есть основная матрица обратима.
, то есть основная матрица обратима.
Теорема Крамера. Невырожденная квадратная система имеет единственное решение. Его можно найти в матричном виде по формуле
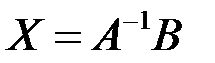 (3.2)
(3.2)
или по формулам Крамера
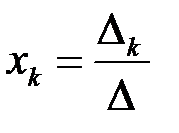 ,
, 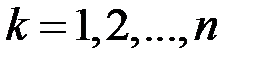 , (3.3)
, (3.3)
являющимися поэлементной записью матричного равенства (3.2).
|
из
5.00
|
Обсуждение в статье: Задачи для самостоятельного решения. В задачах 2.3.3-2.3.4 найти и . 2.3.3 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

