 |
Главная |
Физическое приложение скалярного произведения
|
из
5.00
|
| Рис. 8.3 |
| B |
| C |
| φ |

|
| s |
| Fs |
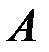 постоянной силы
постоянной силы 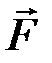 на прямолинейном перемещении из точки
на прямолинейном перемещении из точки  в точку
в точку  называется скалярное произведение вектора силы
называется скалярное произведение вектора силы 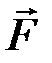 на вектор
на вектор  перемещения (рис. 8.3):
перемещения (рис. 8.3):
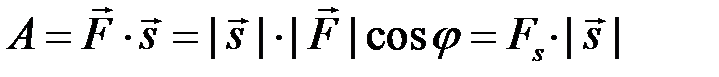 .
.
Впрочем, физики предпочитают модуль вектора обозначать не «вектором в вертикальных черточках», а той же буквой без стрелки:  .
.
Примеры решения задач
8.2.1.Даны длины векторов  ,
, 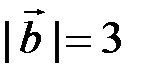 и угол
и угол  . Найти:
. Найти:
1)  , ,
| 2)  , ,
| 3) 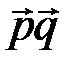 , ,
| 4)  , если , если  , , 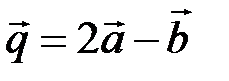 . .
|
◄ Используя выражение (8.7) длины вектора и (8.8) угла между векторами через скалярное произведение и свойства скалярного произведения, имеем
1) 


2) 
3)  ;
;
4) 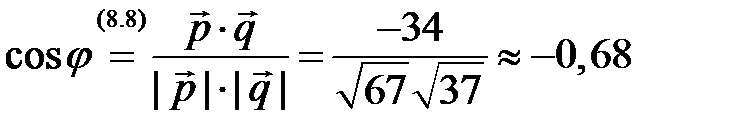 ;
;  . ►
. ►
8.2.2.Дан вектор  . 1) Найти его длину; 2) нормировать вектор; 3) указать направляющие косинусы вектора.
. 1) Найти его длину; 2) нормировать вектор; 3) указать направляющие косинусы вектора.
◄ 1) Длина вектора 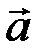 :
:  .
.
2) Нормируем вектор:  – орт вектора
– орт вектора 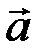 .
.
3) Согласно (8.11) направляющие косинусы вектора 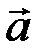 :
:
 ,
,  , и
, и  (рис. 8.2). ►
(рис. 8.2). ►
8.2.3.Даны векторы  и
и  в базисе
в базисе  . Найти:
. Найти:
1) скалярное произведение  ; 2) угол между векторами
; 2) угол между векторами  ; 3) проекции
; 3) проекции  и
и 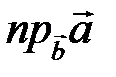 .
.
◄ 1)  ;
;
2) 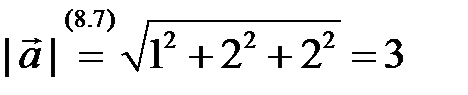 ,
,  ;
;
 ,
,  рад;
рад;
3) 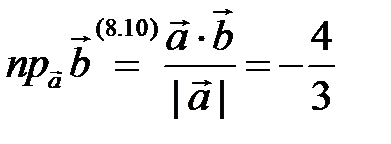 ,
, 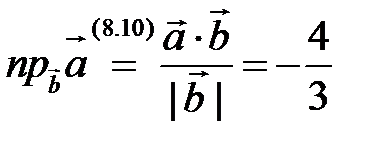 . ►
. ►
8.2.4.В треугольнике  , где
, где  ,
,  ,
, 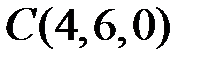 , найти длины сторон, угол
, найти длины сторон, угол  , длину медианы
, длину медианы  (рис. 8.4).
(рис. 8.4).
| A |
| B |
| C |
| M |
| Рис. 8.4 |
 ,
,  и
и  по формуле (7.1), то есть, вычитая из координат концов векторов координаты их начал:
по формуле (7.1), то есть, вычитая из координат концов векторов координаты их начал:  ,
, 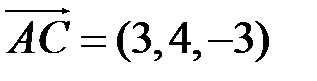 и
и  .
.
2) Длины сторон находим как длины соответствующих векторов по формуле (8.7):  ,
,  и
и  .
.
3) Так как  , то угол
, то угол  – прямой.
– прямой.
4) Так как  – середина
– середина  , то
, то 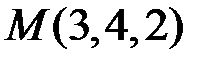 и
и  . Тогда
. Тогда  .
.
8.2.5.Даны координаты точек на плоскости: 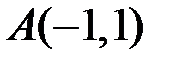 ,
,  ,
,  ,
,  . Убедиться в том, что четырехугольник ABCD является квадратом.
. Убедиться в том, что четырехугольник ABCD является квадратом.
| A |
| B |
| C |
| D |
| O |
| x |
| y |
| Рис. 8.5 |
1. Используя формулу (7.1), то есть, вычитая из координат концов векторов координаты их начал, найдем координаты векторов 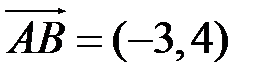 ,
,  и
и  .
.
2. 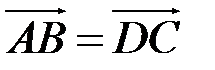 . Значит, ABCD – параллелограмм.
. Значит, ABCD – параллелограмм.
3. Скалярное произведение векторов  и
и  найдем по формуле (8.6), в которой надо опустить третье слагаемое:
найдем по формуле (8.6), в которой надо опустить третье слагаемое:  . Следовательно,
. Следовательно,  . Таким образом, параллелограмм ABCD является прямоугольником.
. Таким образом, параллелограмм ABCD является прямоугольником.
4. Длины векторов найдем по формуле (8.7), где следует опустить третье слагаемое:  ,
,  . Следовательно, прямоугольник ABCD является квадратом. ►
. Следовательно, прямоугольник ABCD является квадратом. ►
8.2.6.Найти значения параметра λ, при которых векторы  и
и  ортогональны.
ортогональны.
◄ Вычислим скалярное произведение  и потребуем выполнения условия ортогональности векторов (8.9):
и потребуем выполнения условия ортогональности векторов (8.9):

При  векторы
векторы 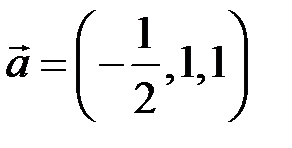 и
и 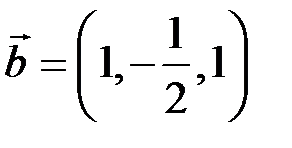 ортогональны, причем это единственное значение λ, при котором
ортогональны, причем это единственное значение λ, при котором 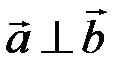 . ►
. ►
8.2.7.Найти координаты вектора 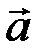 в базисе
в базисе  , если
, если  ,
,  ,
,  ,
,  .
.
◄ Из (8.12), учитывая условие  , находим
, находим
 .
.
По формулам (8.11) находим координаты вектора
 ,
,  ,
, 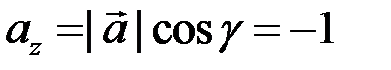 ,
,  . ►
. ►
|
из
5.00
|
Обсуждение в статье: Физическое приложение скалярного произведения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

