Тема 15. Оценка надежности результатов множественной регрессии и корреляции

Оценка статистической значимости и надежности уравнения множественной регрессии осуществляется с помощью - критерия Фишера. Механизм проведения оценки аналогичен оценке значимости уравнения линейной парной регрессии, только:

, где

- число факторов перед переменными;

- объем выборки (количество наблюдений);

- показатель множественной детерминации.

Наряду с оценкой уравнения множественной регрессии в целом производится оценивание статистической значимости фактора, дополнительно включенного в регрессионную модель. В качестве такой оценке используется частный - критерий 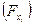. Использование данного критерия основано на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора в модель, с остаточной дисперсией, найденной по регрессионной модели в целом.

В общем виде частный - критерий может быть найден с помощью формулы

Далее критическое значение может быть найдено по формулам:

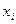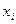Если , то дополнительное включение фактора в модель является статистически оправданным и коэффициент «чистой регрессии» , стоящий фактором является статистически значимым, т.е. .

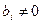Если , то дополнительное включение фактора 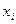в модель не увеличивает существенно долю объясненной вариации результативного признака , т.е. включение фактора 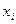является нецелесообразным и коэффициент «чистой регрессии» статистически незначим.

Значение частных - критериев получены в результате проведения дисперсного анализа данных и представляют в виде таблицы дисперсного анализа.

Например, Для уравнения линейной множественной регрессии в таблице приводят следующие значения - критериев:

1) общий - критерий, который оценивает качество двухфакторной модели в целом;

2) оценивается значимость уравнения парной регрессии при условии, что остаточная дисперсия совпадает с остаточной дисперсией для двухфакторной модели;

3) частный - критерий , который оценивает статистическую значимость дополнительного включения фактора в модель после введения фактора .

В результате этого, в таблице дисперсионного анализа источники вариации, соответствующие регрессии можно разложить на две составляющие:

1) составляющая, обусловленная фактором ;

2) составляющая, обусловленная дополнительное включение фактора после включения фактора . Поэтому число степеней свободы, соответствующие множественной регрессии распадается на две единицы. Первая из которых соответствует регрессии, обусловленной фактором , а вторая – регрессия, обусловленная дополнительным включением фактора . Так же в этом случае соответствующие суммы квадратов отклонений могут быть определены по формулам:

1) регрессионная сумма, соответствующая уравнению множественной регрессии

2) регрессионная сумма, обусловленная включением фактора в модель

3) сумма квадратов, обусловленная дополнительным включением фактора в модель

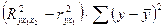
Если уравнение множественной регрессии содержит более двух факторов, то последовательно определяют следующие - критерии:

1) - критерий для уравнения с одним фактором ;

2) - критерий для дополнительного включения фактора в модель после включения фактора ;

3) - критерий для дополнительного введенного фактора в модель после включения факторов , и т.д.;

………………………………………………………………………………

) - критерий для дополнительного включенного фактора в модель после включения факторов , , …, .

В этом случае - критерий для дополнительного включения промежуточного фактора называется последовательным, а - критерий для последней включенной переменной является частным - критерием. Аналогично линейной парной регрессии для множественной регрессии справедлива формула:

, где

- значение - статистики Стьюдента для коэффициента «чистой регрессии»;

- значение частного - критерия.

Последовательные - критерии используются только на определенной стадии формирования модели.

Оценка статистической значимости коэффициентов «чистой регрессии» :

1) находится средняя квадратическая ошибка (стандартная ошибка) параметра

2) находят фактическое значение - критерия

3) находим критическое значение - критерия

4) если , то параметр 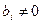(значим и надежен), если 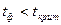, то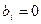

Оценку коэффициента множественной корреляции можно определить через сравнение скорректированного коэффициента корреляции с его табличным значением при соответствующем уровне значимости и числе степеней свободы .

Значимость частных показателей корреляции можно оценить сравнением с их табличными значениями.