 |
Главная |
Классификация поверхностей второго порядка
|
из
5.00
|
Определение. Поверхностью второго порядка в пространстве будем называть множество точек, которое в некоторой декартовой системе координат может быть задано алгебраическим уравнением второго порядка, то есть уравнением вида
a11x2 + a22y2 + a33z2 + 2a12xy + 2a13xz + 2a23yz + 2b1x + 2b2y + 2b3z + c = 0 (*), где a112 + a222 + a332 + a122 + a132 + a232 ≠ 0.
Лемма (о корректности определения).
Понятие поверхности второго порядка не зависит от выбора декартовой системы координат, то есть если некоторое множество задается алгебраическим уравнением второго порядка в некоторой декартовой системе координат, то и в любой другой декартовой системе координат это множество задается алгебраическим уравнением второго порядка.
Доказательство.
Аналогично случаю кривых второго порядка
Теорема (о классификации поверхностей второго порядка) (Без доказательства)
Для любой поверхности второго порядка существует декартова система координат такая, что уравнение данной кривой в этой системе будет иметь один из следующих видов (и других поверхностей второго порядка не существует):
| № п.п. | уравнение | название |
| |  = 1, a > 0, b > 0, c > 0 = 1, a > 0, b > 0, c > 0
| эллипсоид |
| |  = 0, a > 0, b > 0, c > 0 = 0, a > 0, b > 0, c > 0
| точка (начало координат O (0, 0 ,0) |
| |  = -1, a > 0, b > 0, c > 0 = -1, a > 0, b > 0, c > 0
| Æ |
| |  = 1, a > 0, b > 0, c > 0 = 1, a > 0, b > 0, c > 0
| однополостный гиперболоид |
| |  = 0, a > 0, b > 0, c > 0 = 0, a > 0, b > 0, c > 0
| конус |
| |  = -1, a > 0, b > 0, c > 0 = -1, a > 0, b > 0, c > 0
| двуполостный гиперболоид |
| | 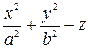 = 0, a > 0, b > 0 = 0, a > 0, b > 0
| эллиптический параболоид |
| | 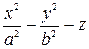 = 0, a > 0, b > 0 = 0, a > 0, b > 0
| гиперболический параболоид |
| |  , a > 0, b > 0 , a > 0, b > 0
| эллиптический цилиндр |
| |  , a > 0, b > 0 , a > 0, b > 0
| прямая (ось (Oz)) |
| |  , a > 0, b > 0 , a > 0, b > 0
| Æ |
| |  , a > 0, b > 0 , a > 0, b > 0
| гиперболический цилиндр |
| |  , a > 0, b > 0 , a > 0, b > 0
| две пересекающиеся плоскости (  ) )
|
| |  , a > 0 , a > 0
| параболический цилиндр |
| |  , a > 0 , a > 0
| две параллельные плоскости (  ) )
|
| |  , a > 0 , a > 0
| плоскость (  ) )
|
| |  , a > 0 , a > 0
| Æ |
Определение. Уравнения, указанные в таблице теоремы классификации, принято называть каноническими уравнениями поверхностей второго порядка.
Определение. Сечением поверхности второго порядка будем называть пересечение этой поверхности и некоторой плоскости.
Лемма. Любое сечение поверхности второго порядка - это кривая второго порядка.
Доказательство.
1) Рассмотрим сечение поверхности, заданной уравнением (*) плоскостью z = 0.
Ясно, что в плоскости z = 0 мы получим кривую второго порядка, заданную уравнением a11x2 + 2a12xy + a22y2 + 2b1x + 2b2y + c = 0.
2) Рассмотрим сечение поверхности второго порядка плоскостью a.
Существует преобразование декартовой системы координат такое, что плоскость a будет задаваться в новой системе координат уравнением z = 0 (то есть плоскость a будет совпадать с плоскостью (Oxy)). Так что сечение поверхности второго порядка плоскостью a будет так же кривой второго порядка.
Замечание. Факт, изложенный в предыдущей лемме, лежит в основе изучения поверхностей второго порядка методом сечений. По тому, какие сечения мы можем получить, можно составить представление о форме поверхности.
|
из
5.00
|
Обсуждение в статье: Классификация поверхностей второго порядка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

