Исследование поверхностей второго порядка

(методом сечений)

 

Эллипсоид

- поверхность второго порядка, которая в некоторой декартовой системе координат задается уравнением вида = 1 (*) (где a > 0, b > 0, c > 0).

 

Уравнение (*) называется каноническим уравнением эллипсоида, и именно по этому уравнению мы будем исследовать форму эллипсоида.

 

1) По уравнению (*) видно, что эллипсоид симметричен относительно координатных плоскостей, координатных осей и начала координат.

Действительно, если точка M(x,y,z) принадлежит эллипсоиду, то есть ее координаты удовлетворяют уравнению (*), то и точки M₁(-x,y,z), M₂(x,-y,z), M₃(x,y,-z), M₄(-x,-y,z), M₅(-x,y,-z), M₆(x,-y,-z) и M₇(-x,-y,-z) принадлежат эллипсоиду, так как их координаты удовлетворяют уравнению (*).

 

2) По уравнению (*) видно, что для координат точек эллипсоида справедливы неравенства: | x | £ a, | y | £ b, | z | £ c, то есть эллипсоид рассоложен внутри прямоугольного параллелепипеда, заданного системой неравенств .

 

РИС. 49 (1,2,3)

 

 

3) Сечения плоскостями z = z₀.

Согласно пунктам 1,2 достаточно рассмотреть случай 0 £ z₀ £ c.

z = 0 (плоскость (xOy)):

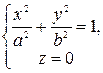- эллипс с полуосями a и b;

 

z = c (плоскость параллельная плоскости (xOy)):

- точка с координатами (0,0,c);

 

 

z = z₀ , 0 < z₀ < c (плоскость параллельная плоскости (xOy)):

Û (где l > 0, l² = ) -

- эллипс с полуосями la и lb.

При этом, чем ближе значение z₀ к c, тем ближе l к нулю, то есть тем меньше полуоси la и lb эллипса, который мы получаем в сечении.

 

4) Сечения плоскостями x = x₀.

Согласно пунктам 1,2 достаточно рассмотреть случай 0 £ x₀ £ a.

x = 0 (плоскость (yOz)):

- эллипс с полуосями b и с;

 

x = a (плоскость параллельная плоскости (yOz)):

- точка с координатами (a,0,0);

 

 

x = x₀ , 0 < x₀ < a (плоскость параллельная плоскости (yOz)):

Û (где l > 0, l² = ) -

- эллипс с полуосями lb и lc.

При этом, чем ближе значение x₀ к a, тем ближе l к нулю, то есть тем меньше полуоси lb и lc эллипса, который мы получаем в сечении.

5) Сечения плоскостями y = y₀.

Согласно пунктам 1,2 достаточно рассмотреть случай 0 £ y₀ £ b.

y = 0 (плоскость (xOz)):

- эллипс с полуосями a и с;

 

y = b (плоскость параллельная плоскости (xOz)):

- точка с координатами (0,b,0);

 

 

y = y₀ , 0 < y₀ < b (плоскость параллельная плоскости (xOz)):

Û (где l > 0, l² = ) -

- эллипс с полуосями la и lc.

При этом, чем ближе значение y₀ к b, тем ближе l к нулю, то есть тем меньше полуоси la и lc эллипса, который мы получаем в сечении.

 

РИС. 50

эллипсоид

 

Замечания.

1) При a = b = c эллипсоид - это сфера с центром в начале координат и радиусом a.

2) При a = с эллипсоид является эллипсоидом вращения, получается вращением эллипса , лежащего в плоскости (xOy), вокруг оси (Oy).

Случаи a = b, b = c аналогичны.

 

Эллиптический цилиндр

- поверхность второго порядка, которая в некоторой декартовой системе координат задается уравнением вида (**) (где a > 0, b > 0).

 

1) По уравнению (**) видно, что эллиптический цилиндр симметричен относительно координатных плоскостей, координатных осей и начала координат.

 

2) По уравнению (**) видно, что для координат точек эллиптического цилиндра справедливы неравенства: | x | £ a, | y | £ b.

 

3) Сечения плоскостями z = z₀ (z₀ - константа).

Согласно пунктам 1,2 достаточно рассмотреть случай z₀ ³ 0.

(плоскость (xOy) или плоскость параллельная плоскости (xOy)):

 

- эллипс с полуосями a и b.

То есть во всех плоскостях параллельных плоскости (xOy) и в самой плоскости (xOy) сечением эллиптического цилиндра являются равные эллипсы с полуосями a и b, центры которых лежат на оси (Oz).

 

4) Сечения плоскостями x = x₀ (x₀ - константа).

Согласно пунктам 1,2 достаточно рассмотреть случай 0 £ x₀ £ a.

x = 0 (плоскость (yOz)):

Û - две параллельные прямые;

 

x = a (плоскость параллельная плоскости (yOz)):

Û - прямая;

 

 

x = x₀ , 0 < x₀ < a (плоскость параллельная плоскости (yOz)):

Û (где l > 0, l² = ) - две параллельные прямые.

Заметим, что в сечении мы получаем прямые параллельные оси (Oz), то есть все эти прямые попарно параллельны (принадлежат одному параллельному пучку).

 

5) Сечения плоскостями y = y₀ (случай аналогичен предыдущему).

 

 

 

РИС. 51 эллиптический цилиндр

Замечания.

1) При a = b эллиптический цилиндр является эллиптическим цилиндром вращения, получается вращением прямой, лежащей в плоскости (yOz) и параллельной оси (Oz), вокруг оси (Oz).

2) Сечения плоскостями x = const и y = const - прямые из одного параллельного пучка, эти прямые называют прямолинейные образующими эллиптического цилиндра.