Коинтеграция модели коррекции ошибок

Если 1 из рядов стац., а второй интегрированный 1-го порядка, то нет смысла строить модель авторегрессии.0

y_t I(1), x_t I(1)- интегр.ряды 1-го порядка.Если для любого by_t-bx_t I(1)(т.е. рядостатков нестац.), то регрессия у на х явл-ся фиктивной. Когда разность явл-ся стац.рядом y_t-bx_t I(0), то ряды y_t и x_t- коинтегрированные ряды, а вектор (1,b)-коинтегрирующий вектор.=>β₁x_t+β₂y_t I(0).

Если векторβ=( β₁, β₂)не=0явл-ся коинтегрирующим вектором , то и вектор вида c=const cβ=( cβ₁,cβ₂)тоже будет коинтегрирующим.

Пусть имеется n-мерный случайный вектор x, компонетны кот. это нестацион. временные рядыХ= .Если эти переменные x_1t ,….,x_nt взаимосвязаны, то их изменения во времени должны быть опред.образом согласованны, т.е. траектории этих рядов не отдаляются далеко друг от друга. Если для эк.системы сущ. равновесие(состояние эк.системы, при кот.воздействие разнонапр.сил взаимно погашается таким образом, что наблюдаемые св-ва системы ост-ся неизменными ), то переменные x_1t ,….,x_nt должны удовлетворять опред. ограничениям.

β`x=0(их лин.комбинация).Это тождество описывает зависимость между переменными,кот.имеют место в долгоср.перспективе в состоянии равновесия.

β`x=z_t-отклонение от равнов.системы в конкр.мрмент времени t. z_t-случ.величина, обусловл.действием в момент времени t краткоср. факторов – неравновесная ошибка.

Относительно z_t след.предположения:

-E(z_t)=0 -D(z_t)<< 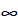. Говорят,что компоненты вектора х явл-ся коинтегриров.порядка d и b и обозн-ся CI(d,b), если а) все компоненты вектора х явл-ся интегр.порядка d

b)сущ.βне=0,что z_t=β`x_t~I(d-b)b>0,β-коинтегр-щий вектор(вектор коинтеграции).

Механизм коррекции ошибок:

Пусть х-краткоср. % ставка, у-долгоср.% ставка. Мжду этими ставками сущ. Долгоср. зав-сть след.вида y-βx=0.В каждый момент времени может иметь место отклонение от равнов сост.y_t-bx_t= z_t.Ставки изм-ся согласованно так, что их изменения направленны на восстановление равновесия путем коррекции ошибок z_tв соотнош. y_t-bx_t= z_t.В соотв. с механизмом коррекции ошибок величина и направление изменений % ствок в периоде t должны опред-ся величиной и знаком ошибки z_t-1= y_t-₁-βx_t-1,имевшим местовпредыд.периоде.Для рассмотрения случая модель коррекции ошибок ECM:

∆x_t=α_x(y_t-₁- βx_t-1)+ε_xt, ∆y_t=α_y(y_t-₁- βx_t-1)+ε_yt (*) α_x, α_y>0/

∆x_t, ∆y_t-краткоср.изменение% ставок, ε_xt, ε_yt- процессы белого шума. α_x, α_y, β-параметры.

Соотношение (*) описывает краткоср. зав-сть между анализируемыми эеон.переменными.Если y_t-₁- βx_t-1>0, то в след.периоде краткоср. ставки должны возрасти, а долгоср. понизиться и наоборот. Если y_t-₁- βx_t-1<0 , то коррекции ошибок нет, а изменения ∆x_t, ∆y_tобусловлены только воздействием случ.факторов ε.

Параметры α_x,α_y характеризуют скорость коректировки:чем больше α_x, α_y, тем больше доля отклонения от равновесия за прошлый период кор-ся в след.периоде.Условия αx, α_y не=0 выполняются,если между переменными х и у сущ. Причинная зависимость по Грейнджеру.

Еслиα_хне=0, α_y=0, то у не воияет по Грейнждеру на х, но х оказывает влияние на у.Если α_yне=0, α_х=0, то имеется одностороннее влияние по Гр. Если α_x,α_y=0, то между переменными отсутствует прич.зависимость и модель (*) не явл-ся моделью коррекции ошибок.Представление приращений ∆x_t, ∆y_t, интегриров.времен.рядов x_t и y_t в виде модели ECM возможно, если врем.ряды явл-ся коинтегрированными. Предположим, что ε_xt и ε_yt- процессы белого шума, треб-щиеотсутствия автокор. для времен.рядов модели(*).=> Обобщение модели ECM:

∆y_t= γ₂₀+ α_y(y_t-₁- βx_t-1)+ S γ₂₁(i) ∆x_t-1+S γ₂₂(i) ∆y_t-i+y_xt (**) –модель векторнойавторегрессии для 1-ых разностей.Модели ∆x_t, ∆y_t-векторные модели коррекции ошибок.

Построение ECM с помошью подхода Энгла-Грейнджера:

1.предварит.анализ врем.рядов:исслед.стационарности и опрделение порядка интегриров-сти для врем.рядов , кот. будут исп-ны для постр.модели ECM.Возможны след.ре-ты тестирования:

- х и у стац.врем.ряды

-х и у ряды интегрир. С разным порядком интегрир.

-х и у интегр.врем.ряды с один.порфдком интегрируемости.

2.тестирование коинтегрир-сти врм.рядов с оцениванием долгоср.зав-стиy_t=β₀+ β₁x_t+z_t/

С пом.МНК нах-ся β₀ и β₁.вычисл-ся ряд остатков _t= y_t- ₀- ₁x_t. Если врем ряд остатков _t не стац., то y_t и x_t не коинтегр. И наоборот. Если I(0)-коинтегр. Для тестирования стационарности ряяда остатков тест Дикки-Фуллера.

3.Оценивание параметров и тестирвание адекватности модели коррекции ошибок. Находятся оценки параметров модели вида (**).