Применение производной в экономике

 

В экономике широко применяется понятие эластичности функции. Эластичностью функции y = f(x) относительно переменной x называется величина

Эластичность функции характеризует процент прироста зависимой переменной, соответствующий приращению независимой переменной на 1%.

 

Пример 10. Найти эластичность функции

Решение

Применяя формулу находим

В частности, если, например, x = 2, то Это значит, что если переменная x возрастает на 1%, то переменная y увеличивается на 2,4%.

 

Дифференциал функции

 

Дифференциалом функции y = f(x) в точке называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy или или
dy = f ¢(x)dx, так как dx = Dx. Из второй формулы следует, что

При достаточно малых справедлива приближенная формула

или

Данная формула часто используется в приближенных вычислениях.

 

Пример 11.Найти дифференциал функции

Решение

По формуле находим

 

Тест 6. Дифференциал функции равен:

1)

2)

3)

4)

5)

 

Пример 12.Найти дифференциал функции y = x² + 2x + 2 в точке x = 1.

Решение

По формуле находим

Подставим x = 1 в dy и получим

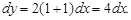
Тест 7. Дифференциал dy функции в точке x = 3 равен:

1)

2)

3) ln 6 dx;

4)

5)

 

Пример 13. Найти приближенное значение

Решение

Нам известно значение равное 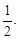Воспользуемся им и формулой В качестве следует взять радианную меру т. е. величину со знаком «минус». Имеем

Dх = –

Поэтому получаем, что

Ответы на тестовые задания

 

Номер теста
Правильный ответ

 

 

Основные теоремы о дифференцируемых функциях

 

Теорема Ферма

 

Теорема. Пусть функция y = f(x) определена в интервале (а; b) и в некоторой точке c Î (а; b) принимает наибольшее (наименьшее) значение. Тогда, если в точке существует производная, то она равна нулю:

Геометрический смысл теоремы: так как то касательная к графику функции в точке М, абсцисса которой равна с, параллельна оси Ox (рисунок 29).

Рисунок 29

 

Замечания:

1. По условию теоремы функция определена в интервале (a; b). В этом промежутке все точки внутренние. Таким образом, точка взята внутри промежутка Х.

2. Если функция принимает наибольшее (наименьшее) значение на конце промежутка, например, в точке а промежутка X = [a; b], и в этой точке существует конечная односторонняя производная, то она может не равняться нулю.

 

Пример 1. Проверить, удовлетворяет ли функция 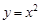условиям теоремы Ферма на отрезке

 

 

Решение

Функция определена на интервале

На концах отрезка функция принимает наибольшее и наименьшее значения: при х = 0 функция принимает наименьшее значение:
f(0) = 0² = 0; при – наибольшее значение:

Условие теоремы не выполнено, поскольку наибольшее (наименьшее) значение функция должна принимать внутри промежутка, а не на его концах.

В результате, хотя функция в точке принимает наибольшее значение и имеет конечную производную: производная в этой точке отлична от нуля:

 

Пример 2.Проверить, удовлетворяет ли функция у = х² условиям теоремы Ферма на отрезке

Решение

Функция определена на интервале

При х = 0 функция принимает наименьшее значение: f(0) = 0² = 0. Это наименьшее значение функция принимает внутри интервала.

Функция у = х² в точке х = 0 имеет конечную производную: которая в этой точке равна нулю:

Таким образом, теорема Ферма применима к функции у = х² на отрезке

 

Тест 1.Пусть функция y = f(x) определена в интервале (a; b) и в некоторой точке c Î (а; b) принимает наибольшее (наименьшее) значение. Тогда, если в точке существует производная, то:

1)

2)

3)

4)

5)

 

Тест 2.Теорема Ферма применима, если:

1) функция y = f(x) определена в интервале (a; b);

2) функция y = f(x) в некоторой точке c Î (а; b) принимает наибольшее (наименьшее) значение;

3) функция y = f(x) определена в интервале (a; b) и в некоторой точке c Î (а; b) принимает наибольшее (наименьшее) значение;

4) функция y = f(x) определена в интервале (a; b) и в некоторой точке c Î (а; b) принимает наибольшее (наименьшее) значение, причем, в точке существует конечная производная

5) в точке c Î (а; b) существует конечная производная

 

Тест 3.Условиям теоремы Ферма на отрезке удовлетворяет функция:

1)

2)

3)

4)

5)

 

Теорема Ролля

 

Теорема. Пусть функция y = f(x) удовлетворяет следующим условиям:

1) непрерывна на отрезке [a; b];

2) дифференцируема на интервале (a; b);

3) на концах интервала принимает равные значения, т. е. f(a) = f(b). Тогда внутри отрезка существует по крайней мере одна точка c Î (а; b), в которой производная равна нулю:

Геометрический смысл теоремы: у графика непрерывной на отрезке и дифференцируемой внутри него функции, принимающей на его концах одинаковые значения, существует точка, в которой касательная к графику функции параллельна оси Ox (рисунок 30).

 

Рисунок 30

 

Пример 3.Проверить, удовлетворяет ли функция y = x – x³ условиям теоремы Ролля на отрезке [0; 1].

Решение

Функция удовлетворяет следующим условиям:

1) непрерывна на отрезке [0; 1];

2) дифференцируема на интервале (0; 1):

3) на концах отрезка принимает равные значения: f(0) = f(1) = 0.

Тогда внутри отрезка [0; 1] должна существовать по крайней мере одна точка c Î (0; 1), в которой производная равна нулю:

Действительно, такая точка существует: при Таким образом, внутри отрезка [0; 1] существует точка где производная равна нулю:

Следовательно, функция y = x – x³ на отрезке [0; 1] удовлетворяет условиям теоремы Ролля.

 

Тест 4.Теорема Ролля применима, если функция y = f(x):

1) непрерывна на отрезке [a; b];

2) дифференцируема на интервале (a; b);

3) на концах интервала принимает равные значения, т. е. f(a) = f(b);

4) непрерывна на отрезке [a; b] и дифференцируема на интервале (a; b);

5) непрерывна на отрезке [a; b], дифференцируема на интервале
(a; b) и на концах интервала принимает равные значения: f(a) = f(b).

 

Тест 5.У графика непрерывной на отрезке и дифференцируемой внутри него функции, принимающей на его концах одинаковые значения, существует точка, в которой касательная к графику функции:

1) параллельна оси Ox;

2) параллельна оси Oу;

3) образует с осью Ox угол a, тангенс которого:

4) образует с осью Oу угол a, тангенс которого:

5) не существует.

 

Тест 6.Условиям теоремы Ролля на отрезке [0; 1] удовлетворяет функция:

1) y = x;

2) y = x²;

3)

4) y = ln x;

5) y = x – x³.

 

Теорема Лагранжа

 

Теорема.Пусть функция y = f(x) удовлетворяет следующим условиям:

1) непрерывна на отрезке [a; b];

2) дифференцируема на интервале (a; b).

Тогда внутри отрезка существует по крайней мере одна точка
c Î [a; b], в которой выполняется равенство

. (1)

Геометрический смысл теоремы: на кривой y = f(x) всегда найдется хотя бы одна точка М с абсциссой, равной с, такая, что касательная, проведенная к кривой в этой точке, будет параллельна хорде, стягивающей дугу АВ (рисунок 31).

 

 

Рисунок 31

 

Теорема Лагранжа является обобщением теоремы Ролля.

Формулу (1) называют формулой Лагранжа, или формулой конечных приращений.

Пример 4. Проверить, может ли быть применима теорема Лагранжа для функции на отрезке

Решение

Функция не определена при следовательно, не является непрерывной на данном отрезке, т. е. первое условие теоремы не выполняется и на данном отрезке теорема Лагранжа не применима.

 

Пример 5.Проверить, может ли быть применима теорема Лагранжа для функции на отрезке

Решение

1.Функция непрерывна на отрезке

2. Проверяем выполнение второго условия теоремы: найдем производную функции

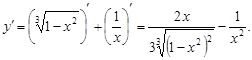
Производная не существует при х = 0 и при х = 1.

В частности, производная не существует в точке

Таким образом, второе условие теоремы не выполняется и на данном отрезке теорема Лагранжа не применима.

 

Пример 6.Проверить, может ли быть применима теорема Лагранжа для функции на отрезке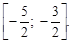

Решение

Функция удовлетворяет следующим условиям:

1)непрерывна на отрезке

2) дифференцируема на интервале

Таким образом, оба условия теоремы выполняются и на данном отрезке теорема Лагранжа применима.

 

Тест 7.Теорема Лагранжа применима, если функция y = f(x):

1) непрерывна на отрезке [a; b];

2) дифференцируема на интервале (a; b);

3) непрерывна на отрезке [a; b] и дифференцируема на интервале (a; b);

4) на концах интервала принимает равные значения: f(a) = f(b);

5) непрерывна на отрезке [a; b], дифференцируема на интервале
(a; b) и на концах интервала принимает равные значения: f(a) = f(b).

 

Теорема Коши

 

Теорема. Пусть функции y = f(x) и 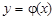удовлетворяют следующим условиям:

1) непрерывны на отрезке [a; b];

2) дифференцируемы на интервале (a; b);

3) j¢(x) ¹ 0 во всех точках интервала (a; b).

Тогда существует по крайней мере одна точка с Î (а; b), в которой выполняется равенство

(2)

Формулу (2) называют формулой конечных приращений Коши.

Замечание. Из условия теоремы следует, что

 

Пример 7.Проверить, может ли быть применима теорема Коши для функций f(x) = x³ и j(x) = x² на отрезке [0; 2].

Решение

Функции удовлетворяют следующим условиям:

1) непрерывны на отрезке [0; 2];

2) дифференцируемы на интервале (0; 2): и при x = 0 производные обращаются в нуль: и но внутри промежутка производные обеих функций отличны от нуля;

3) каждая из функций, например, y = j(x), имеет неравные значения на концах отрезка [0; 2]

т. е.

Таким образом, все условия теоремы Коши на данном отрезке выполняются. Следовательно, теорема Коши на данном отрезке применима.

 

Тест 8.Теорема Коши применима, если функции y = f(x), y = j(x):

1) непрерывны на отрезке [a; b];

2) дифференцируемы на интервале (a; b);

3) во всех точках интервала (a; b);

4) непрерывны на отрезке [a; b], дифференцируемы на интервале (a; b), во всех точках интервала (a; b);

5) непрерывны на отрезке [a; b] и дифференцируемы на интервале (a; b).

 

Правило Лопиталя

 

Применяется для раскрытия неопределенностей вида и

Теорема. Пусть имеем частное двух функций 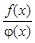, где функции f(x) и j(x) определены в промежутке X = (a; b), имеют конечные производные и в этом промежутке, причем Тогда, если обе функции бесконечно малые или бесконечно большие при х ® а + 0, т. е. если частное 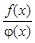при х ® а + 0 представляет собой неопределенность и то при условии, что предел отношения производных существует (конечный или бесконечный).

Правило Лопиталя справедливо и для случая, когда

 

Пример 8.Применив правило Лопиталя, найти предел

Решение

 

Пример 9.Применив правило Лопиталя, найти предел

Решение

Пример 10.Применив правило Лопиталя, найти предел

Решение

 

Пример 11. Применив правило Лопиталя, найти предел

Решение

 

Тест 9. Если y = f(x) и y = j(x) – дифференцируемые бесконечно малые или бесконечно большие функции при х ® а, то имеет место равенство (правило Лопиталя):

1)

2)

3)

4)

5)

 

Тест 10. Для раскрытия неопределенности при вычислении предела применили правило Лопиталя:

1)

2)

3)

 

Ответы на тестовые задания

 

Номер теста
Правильный ответ